The following equations represent transverse waves :
z1=Acos(kx−ωt),
z2=Acos(kx+ωt), z3=Acos(ky−ωt)
Identify the combination (s) of the waves which will produce (i) standing wave(s), (ii) a wave travelling in the direction making an angle of 45∘ with the positive x and positive y axes. In each case, find the positions at which the resultant intensity is always zero.
The correct Answer is:(i) z1 and z2:x=(2n+1)π2k⇒(2n+1)λ/4
where n=0,±1,±2… etc
(ii) z1 and z3:x−y=(2n+1)πk
where n=0,±1,±2,… etc.
(i) Combination of waves producing standing wave : Z1+Z2
(ii) Combination of waves producing a wave travelling along x=y line : Z1+Z3
(iii) Position of nodes in case (i)x=(2n+1)π2k ltbrltgt case (ii) x−y=(2n+1)πk
Topper's Solved these Questions
- WAVES AND OSCILLATIONSBOOK - ALLENCHAPTER - WAVES AND OSCILLATIONSEXERCISE - Part-1(Exercise-05)[A]
28 Videos
- WAVES AND OSCILLATIONSBOOK - ALLENCHAPTER - WAVES AND OSCILLATIONSEXERCISE - Part-1(Exercise-05)[B]
42 Videos
- WAVES AND OSCILLATIONSBOOK - ALLENCHAPTER - WAVES AND OSCILLATIONSEXERCISE - Part-1(Exercise-04)[A]
29 Videos
- SEMICONDUCTORSBOOK - ALLENCHAPTER - SEMICONDUCTORSEXERCISE - Part-3(Exercise-4)
51 Videos
Similar Questions
The following equations represent progressive transverse waves
z1=Acos(ωt−kx)
z2=Acos(ωt+kx)
z3=Acos(ωt+ky)
z4=Acos(2ωt−2ky)
A stationary wave will be formed by superposing
View SolutionConsider the three waves z1,z2andz3 as
z1=Asin(kx−ωt)
z2=Asin(kx+ωt)
z3=Asin(ky−ωt)
Which of the following represents a standing wave?
View Solution
Knowledge Check
Three travelling waves are superimposed. The equations of the wave are
y!=A0sin(kx−ωt),y2=3√2A0sin(kx−ωt+ϕ) and y3=4A0cos(kx−ωt)
find the value of ϕ(given 0≤ϕ≤π/2) if the phase difference between the resultant wave and first wave is π/4Aπ6Bπ3Cπ12DNone of these
Which two of the given transverse waves will give stationary wave when get superimposed?
z1=acos(kx−ωt) (A)
z2=acos(kx+ωt) (B)
z3=acos(ky−ωt) (C)
View SolutionWhich of the following equations can form stationary waves?
(i)y=Asin(ωt−kx) (ii) y=Acos(ωt−kx)
(iii) y=Asin(ωt+kx) (iv) y=Acos(ωt−kx) .
View SolutionWhich of the following functions represent SHM :-
(i) sin2ωt , (ii) sinωt+2cosωt , (iii) sinωt+cos2ωt
View SolutionThe equation y=Asin2(kx−ωt) represents a wave motion with
View SolutionIn a wave motion y=asin(kx−ωt), y can represent
View Solution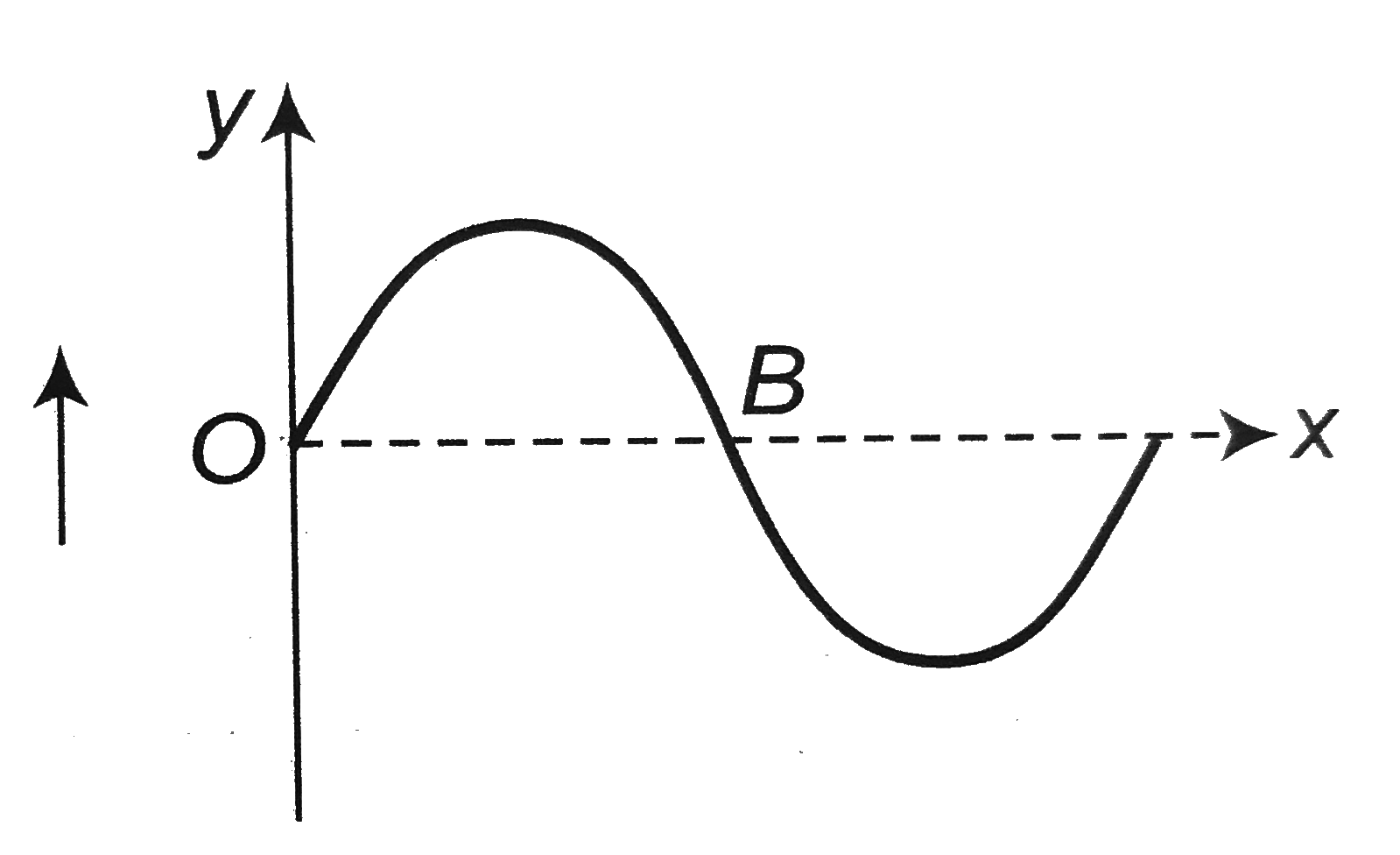
Figure below shows the wave y=Asin(ωt−kx) at any instant travelling in the +ve x-direction. What is the slope of the curve at B?
View SolutionAssertion: Two equations of wave are y1=Asin(ωt−kx)andy2Asin(kx−ωt). These two waves have a phase difference of π.
Reason: They are travelling in opposite directions.
View Solution
