A scientist performs an experiment in order to measure a certain physical quantity and takes 100 observations. He repeats the same experiment and takes 400 observations, by doing so
The possible error remains same
The possible error is doubled
The possible error is halved
The possible error is reduced to one fourth
The correct Answer is:D
To solve the problem, we need to understand how the number of observations affects the mean error in an experiment. Here's a step-by-step breakdown of the solution:
Step 1: Understand the Mean Error Formula
The mean error (Δx_m) is defined as:
Δxm=∑Δxn
where ∑Δx is the total error in the observations, and n is the number of observations.
Step 2: Calculate Mean Error for 100 Observations
Initially, when the scientist takes 100 observations, we can denote the mean error as:
Δxm1=∑Δx100
Step 3: Calculate Mean Error for 400 Observations
When the scientist repeats the experiment and takes 400 observations, the mean error becomes:
Δxm2=∑Δx400
Step 4: Compare the Two Mean Errors
Since the total error ∑Δx remains constant (the possible error does not change), we can compare the two mean errors:
Δxm2=∑Δx400=14⋅∑Δx100=14Δxm1
This shows that the mean error when taking 400 observations is one-fourth of the mean error when taking 100 observations.
Step 5: Conclusion
Thus, by increasing the number of observations from 100 to 400, the possible error is reduced to one-fourth of its original value.
Final Answer
The correct option is that the possible error is reduced to 14.
---
The mean error (Δx_m) is defined as:
Δxm=∑Δxn
where ∑Δx is the total error in the observations, and n is the number of observations.
Initially, when the scientist takes 100 observations, we can denote the mean error as:
Δxm1=∑Δx100
When the scientist repeats the experiment and takes 400 observations, the mean error becomes:
Δxm2=∑Δx400
Since the total error ∑Δx remains constant (the possible error does not change), we can compare the two mean errors:
Δxm2=∑Δx400=14⋅∑Δx100=14Δxm1
This shows that the mean error when taking 400 observations is one-fourth of the mean error when taking 100 observations.
Thus, by increasing the number of observations from 100 to 400, the possible error is reduced to one-fourth of its original value.
The correct option is that the possible error is reduced to 14.
Topper's Solved these Questions
- ERROR AND MEASUREMENTBOOK - ALLENCHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(A)
16 Videos
- ERROR AND MEASUREMENTBOOK - ALLENCHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)
22 Videos
- ERROR AND MEASUREMENTBOOK - ALLENCHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)
22 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)
3 Videos
- KINEMATICSBOOK - ALLENCHAPTER - KINEMATICSEXERCISE - EXERCISE-2
89 Videos
Similar Questions
A scientist performs an experiment and takes 100 readings. He repeats the same experiment and now takes 500 readings, By doing this what is the advantage?
View SolutionA research worker takes 100 observations in an experiment . If he repeats the same experiment by taking 500 observation , how is the probable error affected?
View Solution
Knowledge Check
Assertion : If we perform an experiment in our laboratory today and repeat the same experiment on the same objects under identical conditions after a year, the results are found to be the same .
Reason : The laws of nature do not change with time.AIf both assertion and reason are true and reason is the correct explanation of assertion.BIf both assertion and reason are true but reason is not the correct explanation of assertion.CIf assertion is true but reason is false.DIf both assertion and reason are false.
Look at the picture, understand the experiment and answer the below related questions :
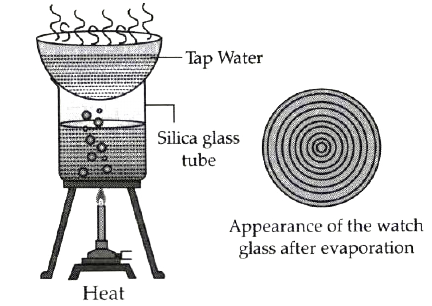
Do we see the same observation when the experiment conducted with rainwater. Why?
View SolutionWhile measuring the speed of sound by performing a resonance column experiment, a student gets the first resonance condition at a column length of 18cm during winter. Repeating the same experiment during summer, she measures the column length to be xcm for the second resonance. Then
View SolutionA student is performing an experiment using a resonance column and a tuning fork of frequency 244s−1. He is told that the air in the tube has been replaced by another gas (assuming that the air column remains filled with the gas). If the minimum height at which resonance occurs is (0.350±0.005)m, the gas in the tube is (Useful information : √167RT=640J1/2mol−1/2,
√140RT=590J1/2mol−1/2. The molar masses M in grams are given in the options. take the values of √10M for each gas as given there.)
View SolutionFollowing experiment was performed by J.J. Thomson in order to measure ratio of charge e and mass m of electron.
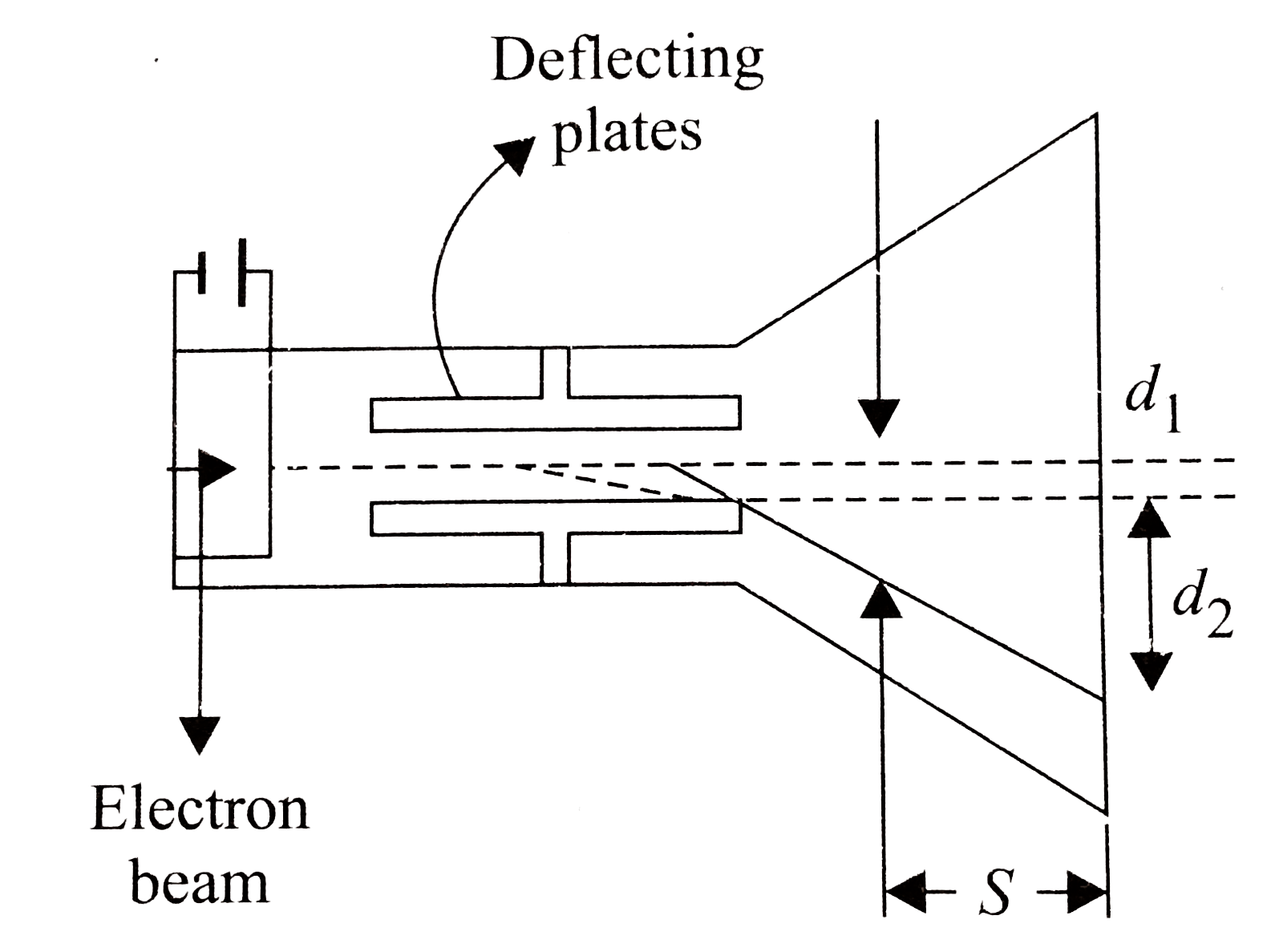
Electrons emitted from a hot filament are accelerated by a potential difference V. As the electrons pass through deflecting plates, they encounter both electric and magnetic fields. the entire region in which electrons leave the plates they enters a field free region that extends to fluorescent screen. The entire region in which electrons travel is evacuated.
Firstly, electric and magnetic fields were made zero and position of undeflected electron beam on the screen was noted. The electric field was turned on and resulting deflection was noted. Deflection is given by d1=eEL22mV2 where L = length of deflecting plate and v = speed of electron.
In second part of experiment, magnetic field was adjusted so as to exactly cancel the electric force leaving the electron beam undeflected. This gives eE = evB. Using expression for d1 we can find out em=2d1EB2L2
If the electron is deflected downward when only electric field is turned on, in what direction do the electric and magnetic fields point in second part of experiment
View SolutionFollowing experiment was performed by J.J. Thomson in order to measure ratio of charge e and mass m of electron.
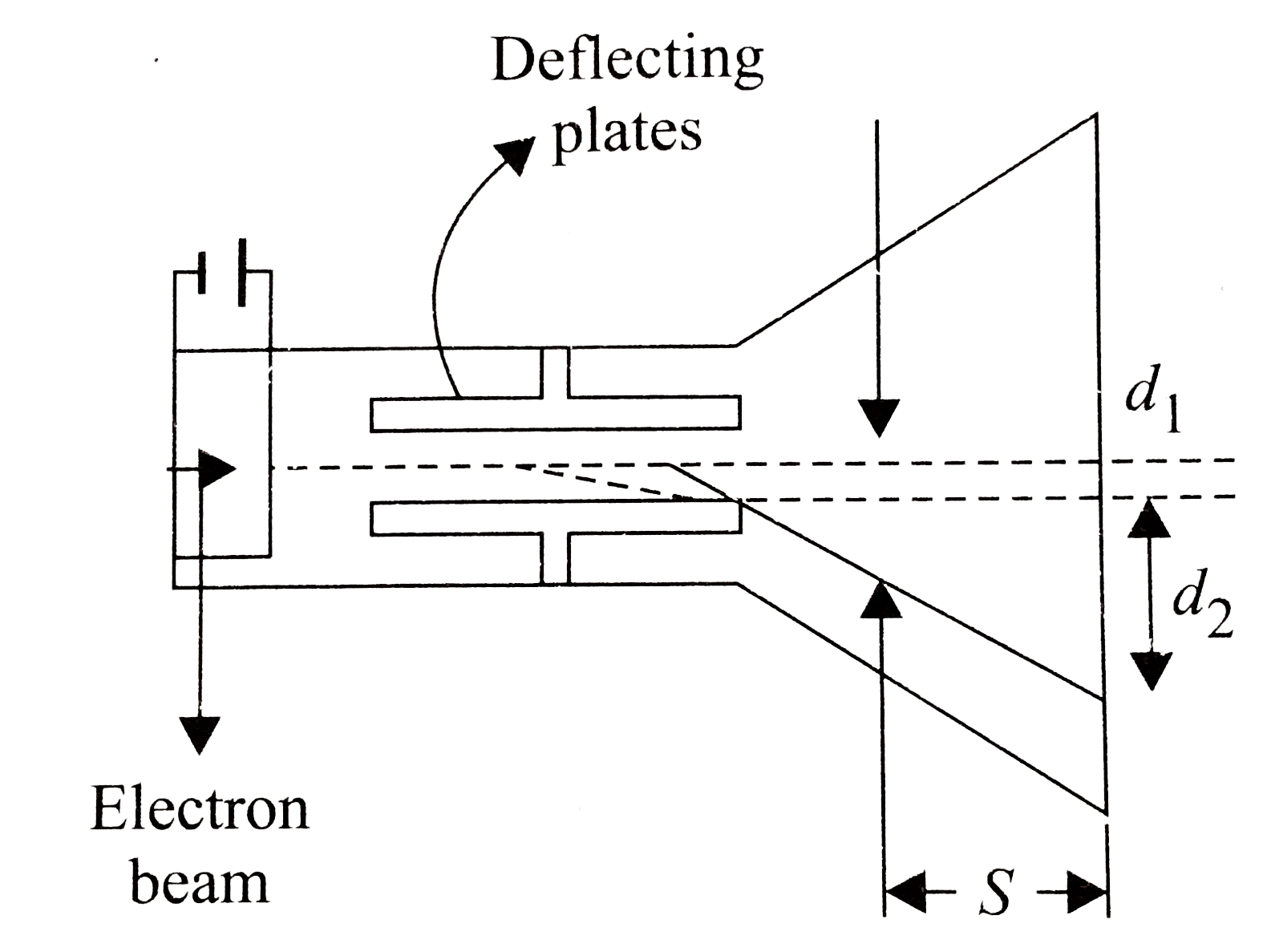
Electrons emitted from a hot filament are accelerated by a potential difference V. As the electrons pass through deflecting plates, they encounter both electric and magnetic fields. the entire region in which electrons leave the plates they enters a field free region that extends to fluorescent screen. The entire region in which electrons travel is evacuated.
Firstly, electric and magnetic fields were made zero and position of undeflected electron beam on the screen was noted. The electric field was turned on and resulting deflection was noted. Deflection is given by d1=eEL22mV2 where L = length of deflecting plate and v = speed of electron.
In second part of experiment, magnetic field was adjusted so as to exactly cancel the electric force leaving the electron beam undeflected. This gives eE=evB. Using expression for d1 we can find out em=2d1EB2L2
A beam of electron with velocity 3×107ms−1 is deflected 2 mm while passing through 10 cm in an electric field of 1800V/m perpendicular to its path. e/m for electron is
View SolutionA scientist performed the gene mapping experiments in maize. He mapped the gene on chromosomes on the basis of % crossing over between different genes. One map unit corresponds to one % crossing over or recombination. Te genes showing more than 50% recombination were not supposed to be linked on same chromosome. In crossing over studies on maize, scientist observed the following % crossing over between A B, C, d- between. A and D 10% between A and C 3% between genes C and D 7% between genes A and B 5% , and between genes C and B 8% on the basis of above observation find out the correct sequence of tenes Alt B, C, and D on chromosomes :-
View SolutionA student performs an experiment for determination of g=4π2lT2l≈1m and the commits an error of ''Deltal' For T he takes the time of n osciilations with the stop watch of least count Δt For which of the following data the measurement of g will be most accurate ?
(a) ΔL=0.5ΔL=0.1,n=20
(B) ΔL=0.5Δt=0.1,n=50
(C) ΔL=0.5,Δt=0.02n=20 (D) ΔL=0.1Δt=0.05n=50 .
View Solution
