Assertion:- In a given situation of arrangement of charges, an extra charge is placed outside the Gaussion surface. In the Gauss Theroem
∮→Ed→s=Q∈ε0Q∈ remains unchanged whereas electric field →E at the site of the element is changed.
Reason:- Electric field →E at any point on the Gaussian surface is due to inside charge only.
If both Assertion & Reason are True & the Reason is a correct explanation of the Assertion.
If both Assertion & Reason are True but Reason is not a correct explanation of the Assertion.
If Assertion is True but the Reason is False.
If both Assertion & Reason are False.
The correct Answer is:C
To solve the question, we need to analyze the assertion and the reason provided in the context of Gauss's law.
1. Understanding Gauss's Law: Gauss's law states that the electric flux through a closed surface (Gaussian surface) is proportional to the charge enclosed within that surface. Mathematically, it is expressed as:
∮→E⋅d→s=Qinϵ0
where ∮→E⋅d→s is the total electric flux through the surface, Qin is the charge enclosed by the surface, and ϵ0 is the permittivity of free space.
2. Analyzing the Assertion: The assertion states that when an extra charge is placed outside the Gaussian surface, the total enclosed charge Qin remains unchanged. This is true because the charge outside the Gaussian surface does not contribute to the enclosed charge. Therefore, the left-hand side of Gauss's law remains equal to Qinϵ0.
3. Electric Field Change: The assertion also mentions that the electric field →E at the site of the element is changed. This is true because the presence of an external charge can influence the electric field at points on the Gaussian surface, even though it does not change the total enclosed charge.
4. Analyzing the Reason: The reason provided states that the electric field →E at any point on the Gaussian surface is due to the inside charge only. This is incorrect because while the enclosed charge determines the total flux, the electric field at any point on the surface can also be influenced by external charges. Therefore, the reason is false.
5. Conclusion: The assertion is true, but the reason is false. Thus, the correct answer to the question is that the assertion is true, and the reason is false.
Final Answer:
- Assertion: True
- Reason: False
∮→E⋅d→s=Qinϵ0
where ∮→E⋅d→s is the total electric flux through the surface, Qin is the charge enclosed by the surface, and ϵ0 is the permittivity of free space.
- Assertion: True
- Reason: False
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - PAPER 399videos
TEST PAPERS
- BOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - Part-1 Physics15videos
TEST PAPERS
- BOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - MATHS14videos
TEST PAPERS
- BOOK - ALLENCHAPTER - TEST PAPER 4EXERCISE - PHYSICS44videos
TEST PAPER 4
- BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)7videos
UNIT & DIMENSIONS, BASIC MATHS AND VECTOR
Similar Questions
Assertion : With the help of Gauss's theorm we can find electric field at any point.
Reason : Gauss's theorem can be applied for any type of charge distribution.View SolutionA : We may have a Gaussian surface in which less number of field lines enter and more field lines come out.
R : The electric field E in the Gauss's law is only due to the enclosed charges.View SolutionA point charge .Q. is placed at a point inside the cone as shown. The flux due to the charge through the curved surface is given as 2Q3ε0. Now another charge .Q. is placed vertically above at the same distance from the base. The flux through the curved surface due to both charges is .
 View Solution
View SolutionA point charge +Q is placed in the vicinity of a conducting surface. Draw the eletric field lines between the surface and the charge
View SolutionAssertion: In a region where uniform electric field exists, the net charge with in volume of any size is zero.
Reason: The electric flux within any closed surface in region of uniform electirc field is zero.View SolutionA charge +q is placed at a distance 'd' from the centre of the uncharged metallic cube of side 'a'. The electric field at the centre of the cube due to induced charges on the cube will be
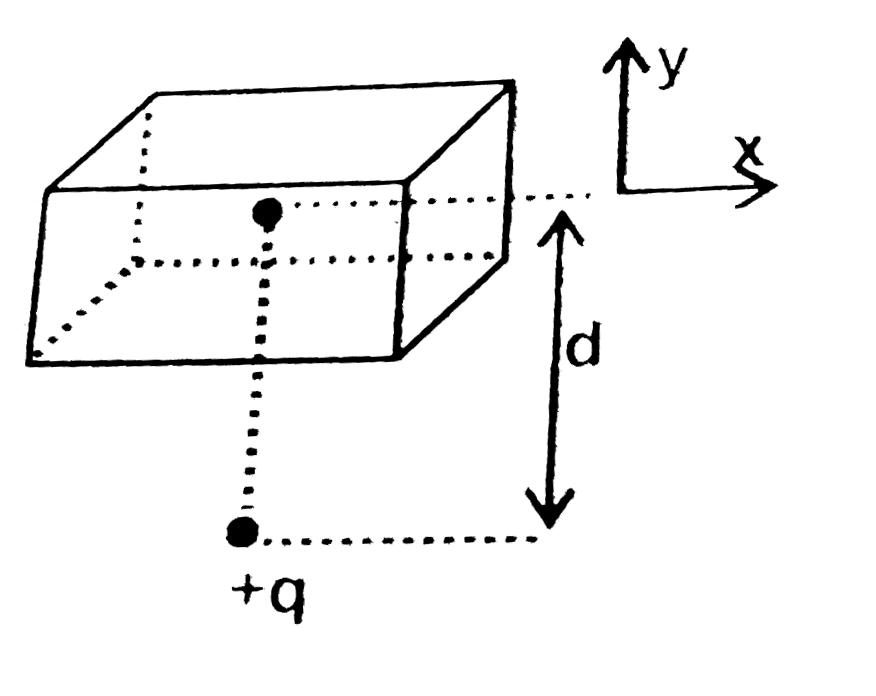 View Solution
View SolutionGauss's law and Coulomb's law , although expressed in different forms , are equivalent ways of describing the relation between charge and electric field in static conditions . Gauss's law is ε0ϕ=qencl,when q(encl) is the net charge inside an imaginary closed surface called Gaussian surface. The two equations hold only when the net charge is in vaccum or air .
If the charge q3 and q4 are displaced (always remaining outside the Gaussian surface), then consider the following two statements :
A: Electric field at each point on the Gaussian surface will remain same .
B: The value of ∮→E.d→A for the Gaussian surface will remain same.View SolutionThe Gaussian surface for calculating the electric field due to a charge distribution is
View SolutionA charge 'Q' is placed at the centre of a hemispherical surface of radius 'R'. The flux of electric field due to charge 'Q' through the surface of hemisphere is
View SolutionAssertion : Electric field inside a conductor is 0.
Reason : Charge is present on surface of conductor.View Solution

