A steel ball strikes a fixed smooth steel plate placed on a horizontal surface at an angle θ with the vertical. If the coefficient of restitution is e, the angle at which the rebound will take place is:
θ
tan−1[tanθe]
etanθ
tan−1[etanθ]
The correct Answer is:B
To solve the problem of a steel ball striking a fixed smooth steel plate at an angle θ with the vertical and rebounding at an angle φ, we can follow these steps:
Step 1: Understand the Components of Velocity
When the steel ball strikes the plate, we can break its initial velocity u into two components:
- The vertical component: usinθ
- The horizontal component: ucosθ
Step 2: Analyze the Collision
Since the plate is smooth and fixed, there is no friction. The vertical component of the velocity will remain unchanged, while the horizontal component will change due to the collision.
Step 3: Apply the Coefficient of Restitution
The coefficient of restitution e relates the velocities before and after the collision. It is defined as:
e=Velocity of separationVelocity of approach
- The velocity of approach (along the line of impact) is ucosθ.
- The velocity of separation (after the collision) will be eucosθ.
Step 4: Determine the Rebound Angle
After the collision, the vertical component of the velocity remains usinθ, and the horizontal component becomes eucosθ.
Using these components, we can find the angle ϕ at which the ball rebounds:
tanϕ=Vertical componentHorizontal component=usinθeucosθ
This simplifies to:
tanϕ=sinθecosθ
Step 5: Find the Angle ϕ
To find ϕ, we take the inverse tangent:
ϕ=tan−1(sinθecosθ)
Final Result
Thus, the angle at which the rebound will take place is:
ϕ=tan−1(tanθe)
When the steel ball strikes the plate, we can break its initial velocity u into two components:
- The vertical component: usinθ
- The horizontal component: ucosθ
Since the plate is smooth and fixed, there is no friction. The vertical component of the velocity will remain unchanged, while the horizontal component will change due to the collision.
The coefficient of restitution e relates the velocities before and after the collision. It is defined as:
e=Velocity of separationVelocity of approach
- The velocity of approach (along the line of impact) is ucosθ.
- The velocity of separation (after the collision) will be eucosθ.
After the collision, the vertical component of the velocity remains usinθ, and the horizontal component becomes eucosθ.
tanϕ=Vertical componentHorizontal component=usinθeucosθ
This simplifies to:
tanϕ=sinθecosθ
To find ϕ, we take the inverse tangent:
ϕ=tan−1(sinθecosθ)
Thus, the angle at which the rebound will take place is:
ϕ=tan−1(tanθe)
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - Part-1 Physics15videos
TEST PAPERS
- BOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - part-2 physics71videos
TEST PAPERS
- BOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - PAPER 260videos
TEST PAPERS
- BOOK - ALLENCHAPTER - TEST PAPER 4EXERCISE - PHYSICS44videos
TEST PAPER 4
- BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)7videos
UNIT & DIMENSIONS, BASIC MATHS AND VECTOR
Similar Questions
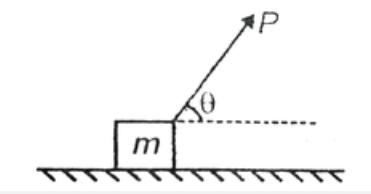
A force P acts on a smooth block of mass m placed on a horizontal floor at an angle θ with with horizontal on the block
 View Solution
View SolutionA ball moving with speed v collides with a horizontal smooth surface at an angle θ with normal to surface as shown in figure. If coefficient of restitution of collision is e, then find v'
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A ball is dropped from a height h on the ground If the coefficient of restitution is e, the height to which the ball goes up after it rebounds for the nth time is
Ahe2nBhenCe2nhDhe2n - Question 2 - Select One
A ball is dropped on to a horizontal plate from a height h = 9 m above it. If the coefficient of restitution is e=1/2, the total distance travelled before the ball comes to rest is
A10 mB15 mC20 mD25 m
A particle strikes a smooth horizontal surface at an angle of 45∘ with a velocity of 100m/s and rebounds. If the coefficient of restitution between the floor and the particle is 0.57 then the angle which the velocity of the particle after it rebounds will make with the floor is
View SolutionA ball is projected in a direction inclined to the vertical and bounces on a smooth horizontal plane. The range of one rebound is R. If the coefficient of restitution is e, then range of the next rebound is
View SolutionA particle strikes a smooth horizontal surface at an angle θ>0 and it rebounds at an angle ϕ as shown
 View Solution
View SolutionA particle of mass m moving with a speed u strikes a smooth horizontal surface at an angle 45∘. The particle rebounds at an angle ϕ with speed v. If coefficient of restituion is 1√3, then angle ϕ is
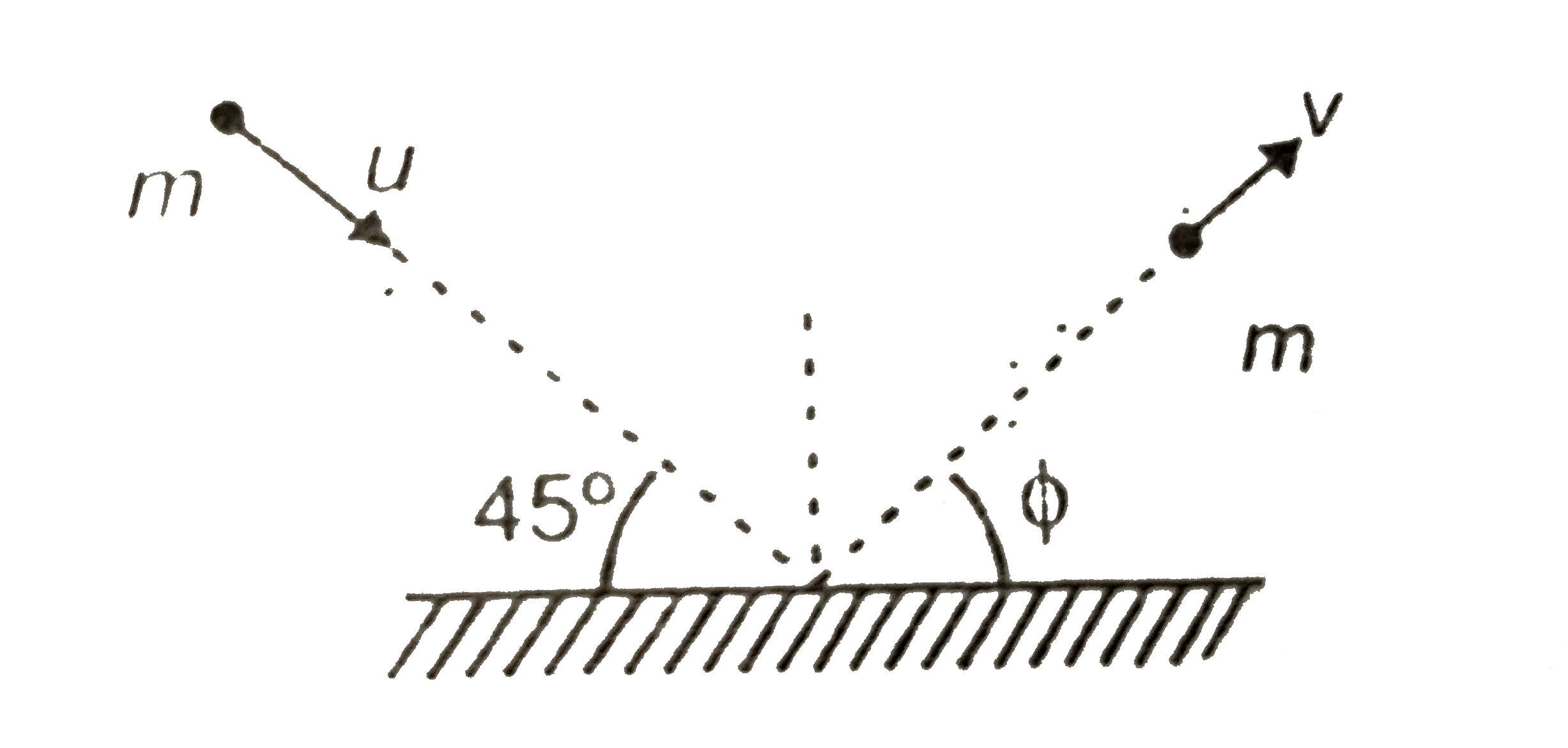 View Solution
View SolutionA particle of mass m moving with a speed u strikes a smooth horizontal surface at an angle 45∘. The particle rebounds at an angle ϕ with speed v. If coefficient of restituion is 1√3, then angle ϕ is
 View Solution
View SolutionA rod of mass m is released on smooth horizontal surface making angle θ with horizontal. Then which of the following statement is correct ?
View Solution

