Find the value of :
The correct Answer is:D
To solve the question, we need to find the values of the following trigonometric functions:
1. sin45∘
2. sin74∘
3. sin15∘
4. cos75∘
Let's go through each step one by one.
Step 1: Find sin45∘
The value of sin45∘ is a well-known trigonometric value:
sin45∘=1√2or√22
Step 2: Find sin74∘
We can express sin74∘ using the double angle formula:
sin74∘=sin(2×37∘)=2sin37∘cos37∘
From trigonometric tables or calculations, we know:
sin37∘=35,cos37∘=45
Substituting these values:
sin74∘=2×35×45=2425
Step 3: Find sin15∘
We can express sin15∘ using the sine difference formula:
sin15∘=sin(45∘−30∘)=sin45∘cos30∘−cos45∘sin30∘
Substituting known values:
sin45∘=1√2,cos30∘=√32,cos45∘=1√2,sin30∘=12
Thus,
sin15∘=1√2⋅√32−1√2⋅12=√3−12√2
Step 4: Find cos75∘
We can express cos75∘ using the cosine addition formula:
cos75∘=cos(45∘+30∘)=cos45∘cos30∘−sin45∘sin30∘
Substituting known values:
cos75∘=1√2⋅√32−1√2⋅12=√3−12√2
Summary of Values
1. sin45∘=1√2
2. sin74∘=2425
3. sin15∘=√3−12√2
4. cos75∘=√3−12√2
2. sin74∘
3. sin15∘
4. cos75∘
The value of sin45∘ is a well-known trigonometric value:
sin45∘=1√2or√22
We can express sin74∘ using the double angle formula:
sin74∘=sin(2×37∘)=2sin37∘cos37∘
From trigonometric tables or calculations, we know:
sin37∘=35,cos37∘=45
Substituting these values:
sin74∘=2×35×45=2425
We can express sin15∘ using the sine difference formula:
sin15∘=sin(45∘−30∘)=sin45∘cos30∘−cos45∘sin30∘
Substituting known values:
sin45∘=1√2,cos30∘=√32,cos45∘=1√2,sin30∘=12
Thus,
sin15∘=1√2⋅√32−1√2⋅12=√3−12√2
We can express cos75∘ using the cosine addition formula:
cos75∘=cos(45∘+30∘)=cos45∘cos30∘−sin45∘sin30∘
Substituting known values:
cos75∘=1√2⋅√32−1√2⋅12=√3−12√2
1. sin45∘=1√2
2. sin74∘=2425
3. sin15∘=√3−12√2
4. cos75∘=√3−12√2
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Part -II Example61videos
MISCELLANEOUS
- BOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Part -II Example Some worked out Examples1videos
MISCELLANEOUS
- BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-78videos
KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)
- BOOK - ALLENCHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-IV8videos
PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT
Similar Questions
Find the values of sin75∘.
View SolutionFind the values of
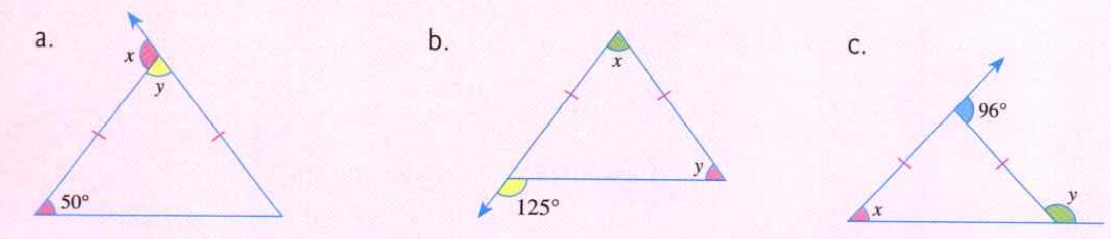
x and y.
View SolutionFind the values of A,B and C
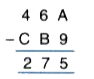 View Solution
View SolutionFind the values of A and B.
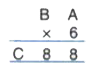 View Solution
View SolutionFind the values of x and y.
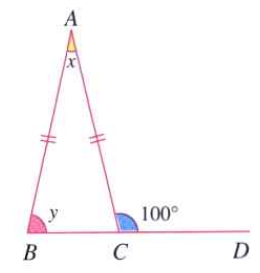 View Solution
View SolutionFind the values of (12)−5
View SolutionFind the values of
(i)(12)−1<br>(ii)13−4View SolutionFind the values of 3−1+4−1
View SolutionFind the values of (12)−1+(13)−1+(14)−1
View Solution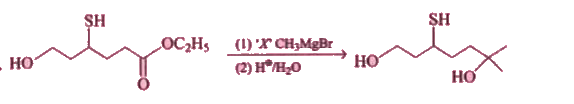
Find out value of 'X'.View Solution

