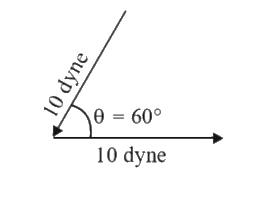
Two force each numerically equal to 10 dynes are acting as shown in the figure, then find resultant of these two vectors.
To solve the problem of finding the resultant of two forces each equal to 10 dynes acting at an angle, we can follow these steps:
Step 1: Identify the Forces and Angle
We have two forces, F1 and F2, each with a magnitude of 10 dynes. The angle between these two forces is given as 120∘ (since one force is in one direction and the other is at an angle of 60 degrees from the first force).
Step 2: Use the Formula for Resultant of Two Vectors
The resultant R of two vectors can be calculated using the formula:
R=√F21+F22+2F1F2cosθ
where θ is the angle between the two forces.
Step 3: Substitute the Values into the Formula
Substituting the values into the formula:
- F1=10 dynes
- F2=10 dynes
- θ=120∘
The equation becomes:
R=√102+102+2⋅10⋅10⋅cos(120∘)
Step 4: Calculate the Cosine of the Angle
We know that:
cos(120∘)=−12
So, substituting this value into the equation gives:
R=√102+102+2⋅10⋅10⋅(−12)
Step 5: Simplify the Expression
Now, simplifying the expression:
R=√100+100−100
R=√100
R=10 dynes
Conclusion
The resultant of the two forces is 10 dynes.
---
We have two forces, F1 and F2, each with a magnitude of 10 dynes. The angle between these two forces is given as 120∘ (since one force is in one direction and the other is at an angle of 60 degrees from the first force).
The resultant R of two vectors can be calculated using the formula:
R=√F21+F22+2F1F2cosθ
where θ is the angle between the two forces.
Substituting the values into the formula:
- F1=10 dynes
- F2=10 dynes
- θ=120∘
R=√102+102+2⋅10⋅10⋅cos(120∘)
We know that:
cos(120∘)=−12
So, substituting this value into the equation gives:
R=√102+102+2⋅10⋅10⋅(−12)
Now, simplifying the expression:
R=√100+100−100
R=√100
R=10 dynes
The resultant of the two forces is 10 dynes.
Topper's Solved these Questions
- MISCELLANEOUSBook:ALLENChapter:MISCELLANEOUSExercise:Part -II Example
Explore 61 Videos
- MISCELLANEOUSBook:ALLENChapter:MISCELLANEOUSExercise:Part -II Example Some worked out Examples
Explore 1 Video
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)Book:ALLENChapter:KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)Exercise:BEGINNER S BOX-7
Explore 8 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT Book:ALLENChapter:PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT Exercise:EXERCISE-IV
Explore 8 Videos
Similar Questions
Two forces , each numerically equal to 10 dyne are acting as shown in the following figure Their resultant is :
View SolutionFour forces are acting on a body as shown in figure. The magnitude of resultant of the forces is
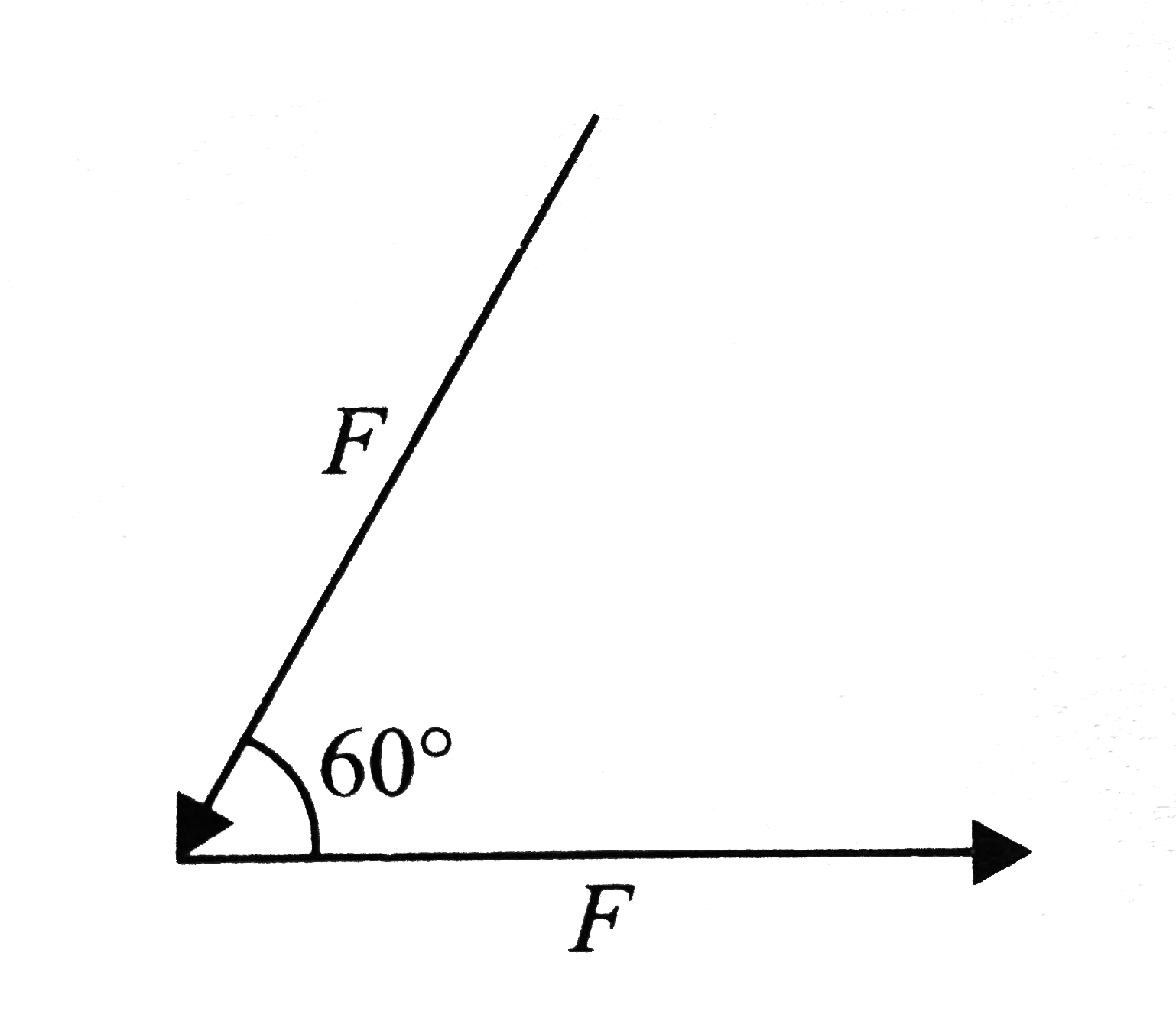
View SolutionTwo forces, each equal to F, act as shown in (figure) Their resultant is
View SolutionFind the resultant of the vectors shown in figure.

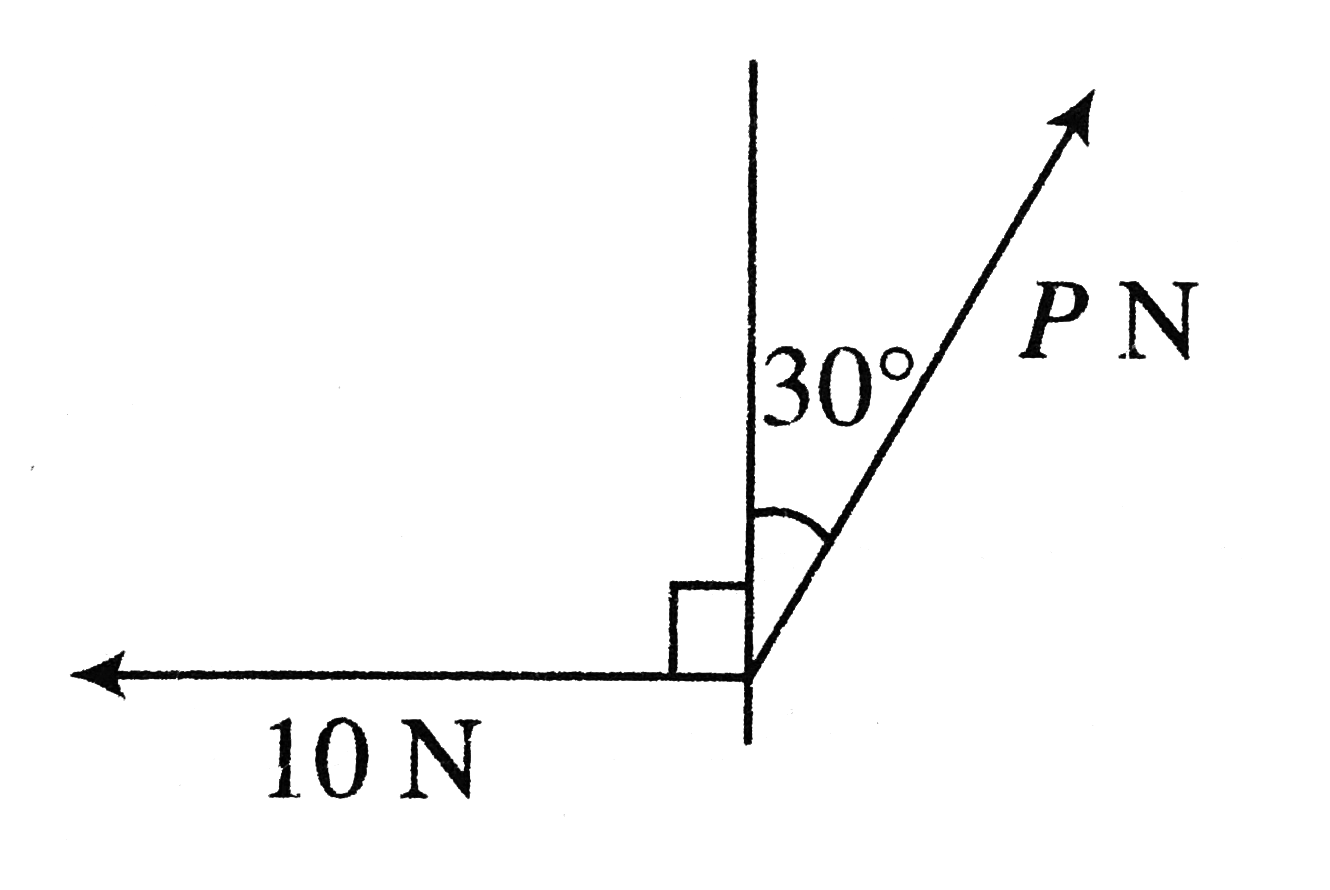
View SolutionTwo horizontal forces of magnitudes of 10N and PN act on a particle. The force of magnitude 10N acts due west and the force of magnitude PN acts on a bearing of 30∘ east of north as shown in (figure) The resultant of these two force acts due north. Find the magnitude of the resultant.
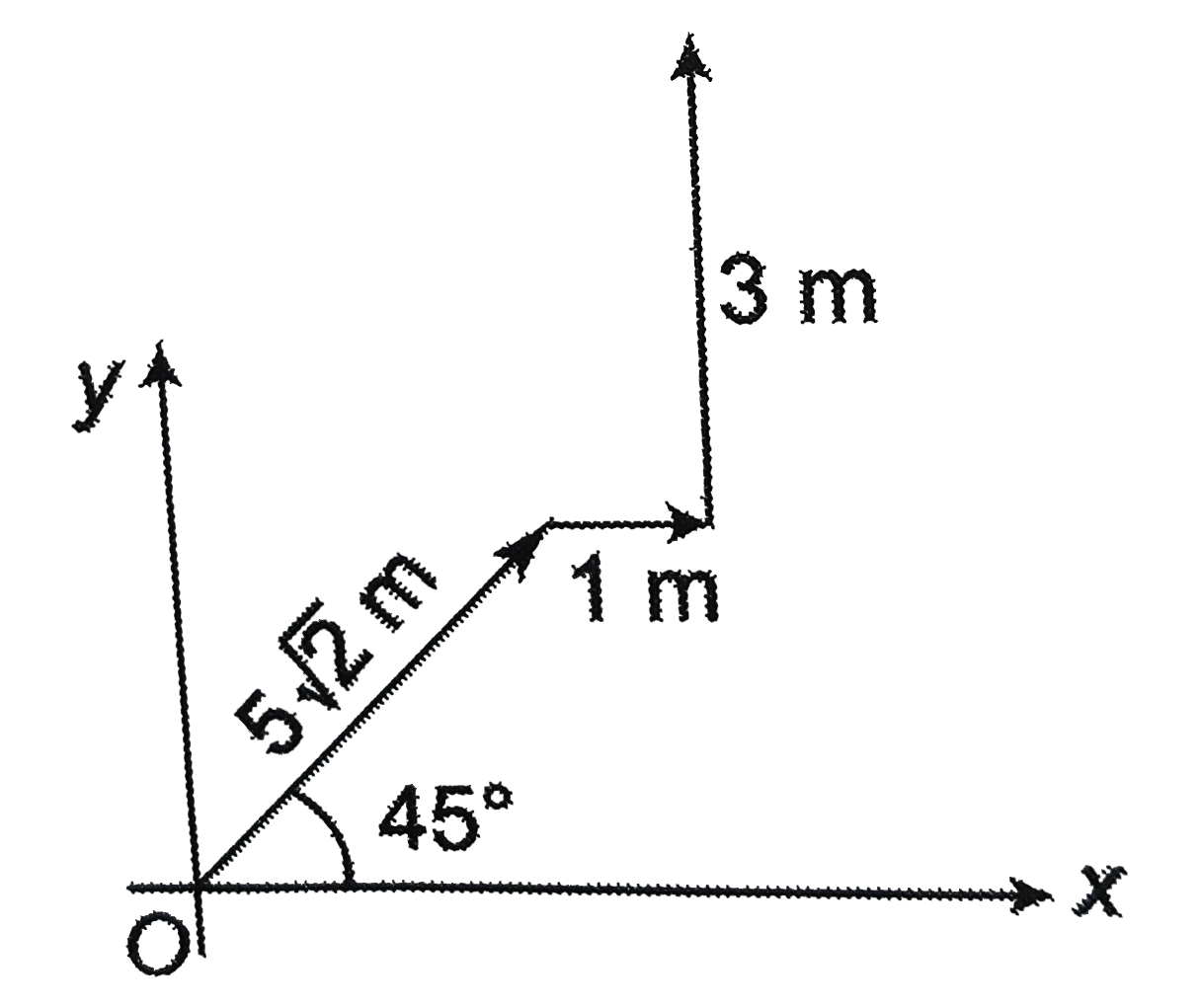
View SolutionFind the resultant of three vectors shown in the figure.
View SolutionA force F is acted on a body as shown in the figure. Find the impulse of the force in first four seconds.

View SolutionFind the resultant of the three vectors shown in figure .
 .
.
View SolutionIn the given figure O is the centre of regular pentagon ABCDE. Five forces each of magnitude F0 are acted as shown in figure. The resultant force is

View SolutionThree co-planar vectors (x−y plane ) having magnitude 3√2,6,10 are shown in the figure. Find the componenent of resultant of three vectors along the x axis as shown.
 .
.
View Solution