Three coplanar vectrors →A,→B and →C have magnitudes 4,3 and 2 respectively. If the angle any two vector is 120∘ then which of the following vector may be equal to 3→A4+→B3+→C2




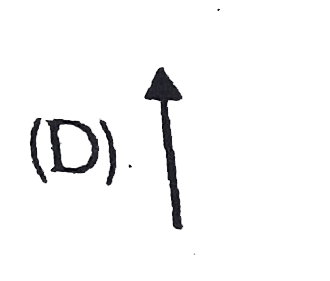
The correct Answer is:B
As ∣∣∣→B3∣∣∣=∣∣∣→C2∣∣∣ so →B3+→C2=−→A4 therefore 3→A4+→B3+→C2=→A2
Topper's Solved these Questions
- MISCELLANEOUSBook:ALLENChapter:MISCELLANEOUSExercise:Part -II Example
Explore 61 Videos
- MISCELLANEOUSBook:ALLENChapter:MISCELLANEOUSExercise:Part -II Example Some worked out Examples
Explore 1 Video
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)Book:ALLENChapter:KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)Exercise:BEGINNER S BOX-7
Explore 8 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT Book:ALLENChapter:PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT Exercise:EXERCISE-IV
Explore 8 Videos
Similar Questions
The magnitudes of vectors →A,→Band→C are 3,4 and 5 unit respectively. If →A+→B=→C, the angle between →Aand→B is
View SolutionFind the angle between two vectors →aand →bwith magnitudes √3and 2 respectively having →a.→b=√6
View SolutionWhat is the angle between vectors →a and →b with magnitudes 2 and 3 respectively ? Given →a.→b=√3 .
View SolutionLet →a, →b, →c be three vectors of magnitudes 3, 4 and 5 respectively. If each one is perpendicular to the sum of the other two vectors, prove that ∣∣→a+→b+→c∣∣=5√2 .
View SolutionThe magnitude of vector →A,→B and →C are respectively 12,5 and 13 unit and →A+→B=→C then the angle between →A and →B is
View SolutionIf →a and →b are two vectors of magnitudes 3 and √23 respectively such that →a×→b is a unit vector. Write the angle between →a and →b.
View SolutionTwo vectors →A and →B have equal magnitudes . If magnitude of →A+→B is equal to n× the magnitude of →A−→B , then the angle between →A and →B is
View SolutionThree vector →A,→B, →C satisfy the relation →A⋅→B=0and →A.→C=0. The vector →A is parallel to
View SolutionThree vector →A,→B, →C satisfy the relation →A⋅→B=0and →A.→C=0. The vector →A is parallel to
View Solution→a,→b,→c are three coplanar unit vectors such that →a+→b+→c=0. If three vectors →p,→q,and→r are parallel to →a,→b,and→c, respectively, and have integral but different magnitudes, then among the following options, |→p+→q+→r| can take a value equal to a. 1 b. 0 c. √3 d. 2
View Solution