An isolated conducting sphere of charge Q and radius R is connected to a similar uncharged sphere (kept at a large distance) by using a high resistance wire. After a long time is the amount of heat loss?
To solve the problem of heat loss when connecting an isolated conducting sphere of charge Q to an uncharged sphere, we will follow these steps:
Step 1: Understand the Initial Conditions
We have two spheres:
- Sphere 1: Charged sphere with charge Q and radius R.
- Sphere 2: Uncharged sphere with charge 0 and radius R.
Step 2: Connect the Spheres
When the two spheres are connected by a high resistance wire, charge will redistribute between them until they reach the same potential.
Step 3: Calculate the Final Charge Distribution
Since the total charge is conserved, the total charge Q will be shared equally between the two spheres:
- Charge on Sphere 1 after connection: Q1=Q2
- Charge on Sphere 2 after connection: Q2=Q2
Step 4: Calculate Initial Energy
The initial energy of the system is only due to Sphere 1 because Sphere 2 is uncharged:
Uinitial=12⋅kQ2R
where k is Coulomb's constant.
Step 5: Calculate Final Energy
After the connection, both spheres have charge Q2 and the potential V on each sphere is:
V=k⋅Q2R=kQ2R
The energy for each sphere is:
Ufinal=2⋅⎛⎜
⎜⎝12⋅k(Q2)2R⎞⎟
⎟⎠=2⋅(kQ28R)=kQ24R
Step 6: Calculate Heat Loss
The heat loss ΔH is the difference between the initial and final energy:
ΔH=Uinitial−Ufinal=(kQ2R)−(kQ24R)
ΔH=kQ2R−kQ24R=4kQ24R−kQ24R=3kQ24R
Final Answer
The amount of heat loss is:
ΔH=3kQ24R
We have two spheres:
- Sphere 1: Charged sphere with charge Q and radius R.
- Sphere 2: Uncharged sphere with charge 0 and radius R.
When the two spheres are connected by a high resistance wire, charge will redistribute between them until they reach the same potential.
Since the total charge is conserved, the total charge Q will be shared equally between the two spheres:
- Charge on Sphere 1 after connection: Q1=Q2
- Charge on Sphere 2 after connection: Q2=Q2
The initial energy of the system is only due to Sphere 1 because Sphere 2 is uncharged:
Uinitial=12⋅kQ2R
where k is Coulomb's constant.
After the connection, both spheres have charge Q2 and the potential V on each sphere is:
V=k⋅Q2R=kQ2R
The energy for each sphere is:
Ufinal=2⋅⎛⎜
⎜⎝12⋅k(Q2)2R⎞⎟
⎟⎠=2⋅(kQ28R)=kQ24R
The heat loss ΔH is the difference between the initial and final energy:
ΔH=Uinitial−Ufinal=(kQ2R)−(kQ24R)
ΔH=kQ2R−kQ24R=4kQ24R−kQ24R=3kQ24R
The amount of heat loss is:
ΔH=3kQ24R
Topper's Solved these Questions
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Part -II Example Some worked out Examples
1 Videos
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Exercise-01
87 Videos
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Question
1 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT BOOK - ALLENCHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-IV
8 Videos
Similar Questions
An isolated conducting sphere of charge Q and radius R is grounded by using a high resistance wire. What is the amount of heat loss ?
View SolutionA charged sphere is connected to a similar uncharged sphere. Then the percentage loss of energy is
View SolutionAn isolated conduction sphere sphere whose radius R=1 m has a charge q=19nC. The energy density at the surfasce of the sphere is
View SolutionA hollow conducting sphere of inner radius r and outer radius 2R is given charge Q as shown in figure, then the

View SolutionA conducting sphere of radius R and carrying a charge Q is joined to an uncharged conducting sphere of radius 2R. The charge flowing between them will be
View SolutionAn unchanged conducting sphere of radius R is placed near a uniformly charge ring of radius R. Total charge on ring is Q. The centre of sphere lies on axis of ring and distance of centre of sphere from centre of ring is R

View SolutionA conducting sphere of radius R is charged to a potential of V volts. Then the electric field at a distance r(>R) from the centre of the sphere would be
View SolutionFind out electric field intensity due to uniformly charged solid non-conducting sphere of volume charge density ρ and radius R at following points :
(i) At a distance r from surface of sphere (inside)
(ii) At a distance r from the surface of sphere (outside)
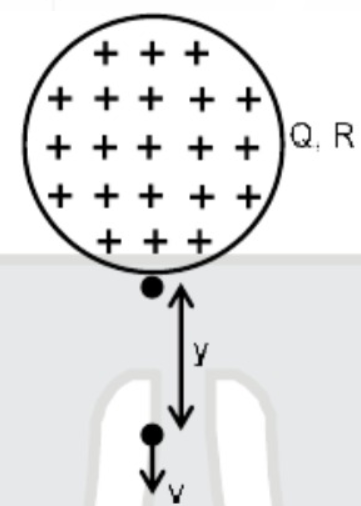
View SolutionA uniformly charged sphere of charge Q and radius R is placed at some height from ground surface and sphere is fixed. Now a charged particle of mass m and charge q is released form rest just below to sphere what will be speed of particle after travelling Y-direction
View SolutionA conducting sphere of radius R, carrying charge Q, lies inside uncharged conducting shell of radius 2R. If they are joined by a metal wire,
View Solution
