A physical quantity x can dimensionally represented in terms of M, L and T that is x=MaLbTc. The quantity time-
May be dimensionally represented in terms of x, M and L if c≠0
May be dimensionally represented in terms of x, M and L if c=0
May be dimensionally represented in terms of x, M and L, irrespective of value of c
Can never be dimensionally represented in terms of x, M and L
The correct Answer is:A
To solve the problem of representing the physical quantity x in terms of dimensions M, L, and T, we will follow these steps:
Step 1: Write the dimensional formula for the physical quantity x
We start with the dimensional representation of the physical quantity x:
x=MaLbTc
where a, b, and c are the powers corresponding to the dimensions of mass (M), length (L), and time (T), respectively.
Step 2: Express time T in terms of x, M, and L
To express time T in terms of x, M, and L, we can rearrange the equation:
Tc=xMaLb
Taking the c-th root on both sides gives us:
T=(xMaLb)1c
Step 3: Simplify the expression for T
Now we can simplify the expression:
T=x1cM−acL−bc
Step 4: Analyze the conditions for representing time T
From the expression derived, we can see that:
- If c≠0, we can express T in terms of x, M, and L.
- If c=0, then x=MaLb and T cannot be expressed in terms of x since T0=1.
Step 5: Evaluate the options given in the question
- Option A: Quantity time may be dimensionally represented in terms of x, M, and L if c≠0. True.
- Option B: Quantity time may be dimensionally represented in terms of x, M, and L if c=0. False.
- Option C: Quantity time may be dimensionally represented in terms of x, M, and L irrespective of the value of c. False.
- Option D: Quantity time can never be dimensionally represented in terms of x, M, and L. False.
Conclusion
The correct option is Option A.
---
We start with the dimensional representation of the physical quantity x:
x=MaLbTc
where a, b, and c are the powers corresponding to the dimensions of mass (M), length (L), and time (T), respectively.
To express time T in terms of x, M, and L, we can rearrange the equation:
Tc=xMaLb
Taking the c-th root on both sides gives us:
T=(xMaLb)1c
Now we can simplify the expression:
T=x1cM−acL−bc
From the expression derived, we can see that:
- If c≠0, we can express T in terms of x, M, and L.
- If c=0, then x=MaLb and T cannot be expressed in terms of x since T0=1.
- Option A: Quantity time may be dimensionally represented in terms of x, M, and L if c≠0. True.
- Option B: Quantity time may be dimensionally represented in terms of x, M, and L if c=0. False.
- Option C: Quantity time may be dimensionally represented in terms of x, M, and L irrespective of the value of c. False.
- Option D: Quantity time can never be dimensionally represented in terms of x, M, and L. False.
The correct option is Option A.
Topper's Solved these Questions
- MISCELLANEOUSBook:ALLENChapter:MISCELLANEOUSExercise:Exercise-03
Explore 1 Video
- MISCELLANEOUSBook:ALLENChapter:MISCELLANEOUSExercise:Exercise-04
Explore 1 Video
- MISCELLANEOUSBook:ALLENChapter:MISCELLANEOUSExercise:Exersice -05(B)
Explore 19 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)Book:ALLENChapter:KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)Exercise:BEGINNER S BOX-7
Explore 8 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT Book:ALLENChapter:PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT Exercise:EXERCISE-IV
Explore 8 Videos
Similar Questions
Knowledge Check
The dimensional formula of physical quantity is [MaLbTc].Then that physical quantity is
Asurface tension if a=1,b=1,c=-2Bforce if a=1,b=1,c=2Cangular frequency if a=0,b=0,c=-1Dspring constant if a=1,b=-1,c=-2
Match the physical quantities given in column I with dimensions expressed interms of mass (M), length (L), time (T) and charge (Q) given in column II and wire the correct answer against the match quantity in labourar form.
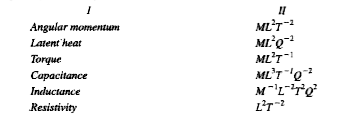
View SolutionA physical quantity X is represented by X=(MxL−yT−z. The maximum percantage errors in the measurement of M,L,andT, respectively , are a%,b%andc%. The maximum percentage error in the measurement of X will be
View SolutionThe physical quantity which has dimensional formula as that of Energymass×length is
View SolutionA physical quantity Q is related to measurable quantities L,M and N as Q=KL−2M2N3, where k is constant. If the % errors in the measurements of L, M and N are respectively 1%, 2% and 1%, then the % error in hc mcasurement of Q is
View SolutionA physical quantity is represented by X=MaLbT−c.If the percentage error in the measurement of M,L and T are α%,β% and γ% to respectively, what is the total percentage error in X?
View SolutionA physical quantity is represented by X=MaLbT−c.If the percentage error in the measurement of M,L and T are α%,β% and γ% to respectively, what is the total percentage error in X?
View SolutionIf the dimensions of a physical quantity are given by MxLyTz, then physical quantity may be
View Solution