Assume that the largest stone of mass 'm' that can be moved by a flowing river depends upon the velocity of flow v, the density d & the acceleration due to gravity g. I 'm' varies as the Kth power of the velocity of flow, then find the value of K.
The correct Answer is:K=6
To solve the problem, we will use dimensional analysis to find the value of K in the relationship between the mass m of the stone that can be moved by the river and the velocity v, density d, and acceleration due to gravity g.
1. Identify the relationship: We know that the mass m of the stone depends on the velocity v, density d, and acceleration due to gravity g. We can express this relationship as:
m=k⋅vK⋅db⋅gc
where k is a constant, and K, b, and c are the powers we need to determine.
2. Write down the dimensions:
- The dimension of mass m is (M).
- The dimension of velocity v is (L)(T−1).
- The dimension of density d is (M)(L−3).
- The dimension of acceleration due to gravity g is (L)(T−2).
3. Express the dimensions:
- For m:
(m)=(M)
- For vK:
(vK)=(LK)(T−K)
- For db:
(db)=(Mb)(L−3b)
- For gc:
(gc)=(Lc)(T−2c)
4. Combine the dimensions:
Combining all the dimensions on the right-hand side, we have:
(M)=(Mb)(LK)(T−K)(M0)(L−3b)(Lc)(T−2c)
This simplifies to:
(M)=(Mb)(LK−3b+c)(T−K−2c)
5. Set up equations for each dimension:
We can equate the powers of each dimension on both sides:
- For mass M:
b=1(Equation 1)
- For length L:
K−3b+c=0(Equation 2)
- For time T:
−K−2c=0(Equation 3)
6. Substitute b into the equations:
From Equation 1, we have b=1. Substitute this into Equation 2:
K−3(1)+c=0⟹K−3+c=0⟹K+c=3(Equation 4)
7. Solve for K and c:
From Equation 3:
−K−2c=0⟹K=−2c(Equation 5)
Substitute Equation 5 into Equation 4:
−2c+c=3⟹−c=3⟹c=−3
Now substitute c=−3 back into Equation 5:
K=−2(−3)=6
8. Final Result:
Thus, the value of K is:
K=6
m=k⋅vK⋅db⋅gc
where k is a constant, and K, b, and c are the powers we need to determine.
- The dimension of mass m is (M).
- The dimension of velocity v is (L)(T−1).
- The dimension of density d is (M)(L−3).
- The dimension of acceleration due to gravity g is (L)(T−2).
- For m:
(m)=(M)
- For vK:
(vK)=(LK)(T−K)
- For db:
(db)=(Mb)(L−3b)
- For gc:
(gc)=(Lc)(T−2c)
Combining all the dimensions on the right-hand side, we have:
(M)=(Mb)(LK)(T−K)(M0)(L−3b)(Lc)(T−2c)
This simplifies to:
(M)=(Mb)(LK−3b+c)(T−K−2c)
We can equate the powers of each dimension on both sides:
- For mass M:
b=1(Equation 1)
- For length L:
K−3b+c=0(Equation 2)
- For time T:
−K−2c=0(Equation 3)
From Equation 1, we have b=1. Substitute this into Equation 2:
K−3(1)+c=0⟹K−3+c=0⟹K+c=3(Equation 4)
From Equation 3:
−K−2c=0⟹K=−2c(Equation 5)
Substitute Equation 5 into Equation 4:
−2c+c=3⟹−c=3⟹c=−3
Now substitute c=−3 back into Equation 5:
K=−2(−3)=6
Thus, the value of K is:
K=6
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Exersice-4[B]14videos
MISCELLANEOUS
- BOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - EXERCISE-5(A)15videos
MISCELLANEOUS
- BOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - DATA SUFFICIENCY QUESTIONS3videos
MISCELLANEOUS
- BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-78videos
KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)
- BOOK - ALLENCHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-IV8videos
PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT
Similar Questions
Assuming that the mass m of the largest stone that can be moved by a flowing river depends upon the velocity v of the water , its density ρ , and the acceleration due to gravity g . Then m is directly proportinal to
View SolutionAssuming that the mass m of the largest stone that can be moved by a flowing river depends upon the velocity υ, of water, its density ρ and acceleration due to gravity g, then m is directly proportional to
View Solution
Knowledge Check
- Question 1 - Select One
A simple pendulum with a bob of mass m oscillates from A to C and back to A such that PB is H. IF the acceleration due to gravity is g, the velocity of bob as it passes through B is
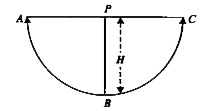 AzeroB2g HCmghD√(2gH)
AzeroB2g HCmghD√(2gH)
It is given that the mass m of the largest stone that can be moved by the folowing river depends upon the velocity v, density ρ and acceleration due gravity g. Using dimensions show that m=kv6ρg3.
View SolutionThe velocity of water wave v may depend on their wavelength λ, the density of water ρ and the acceleration due to gravity g. The method of dimensions gives the relation between these quantities as
View SolutionA ball is thrown vertically upwards. It goes to a height 20 m and then returns to the ground. Taking acceleration due to gravity g to be 10m s−2 ?, find the initial velocity of the ball
View SolutionExperiments reveal that the velocity v of water waves may depend on their wavelength λ, density of water ρ, and acceleration due to gravity g. Establish a possible relation between vandλ,g,ρ.
View SolutionDerive an expression for the time period (T) of a simple pendulum which may depend upon the mass (m) of the bob, length (l) of the pendulum and acceleration due to gravity (g).
View SolutionA ball is thrown vertically upwards. It goes to a height 20 m and then returns to the ground. Taking acceleration due to gravity g to be 10m s−2 ?, find the final velocity of ball on reaching the ground
View SolutionIf the earth were to spin faster, acceleration due to gravity at the poles :
View Solution

