Two balls are moving on the same smooth horizontal plane. Their velocity components along one adge of the square plane are 10√3m/s & 20m/s respectively. Their velocity components along a perpenficular edge are 30m/s & 20m/s. Find the angle between their directions of motion.
The correct Answer is:15∘
To find the angle between the directions of motion of the two balls, we can follow these steps:
Step 1: Identify the velocity components
Let’s denote the velocity components of the first ball as:
- V1x=10√3m/s (along one edge)
- V1y=30m/s (along the perpendicular edge)
For the second ball, the velocity components are:
- V2x=20m/s (along one edge)
- V2y=20m/s (along the perpendicular edge)
Step 2: Calculate the angles of motion
To find the angle of motion for each ball, we can use the tangent function, which relates the opposite side to the adjacent side in a right triangle.
For the first ball:
tan(α)=V1yV1x=3010√3=3010⋅1.732=3017.32≈1.732
Thus, α=tan−1(1.732). We know that tan(60∘)=√3, so:
α=60∘
For the second ball:
tan(β)=V2yV2x=2020=1
Thus, β=tan−1(1). We know that tan(45∘)=1, so:
β=45∘
Step 3: Find the angle between the two directions of motion
The angle θ between the two directions of motion is given by:
θ=α−β=60∘−45∘=15∘
Final Answer
The angle between the directions of motion of the two balls is 15∘.
---
Let’s denote the velocity components of the first ball as:
- V1x=10√3m/s (along one edge)
- V1y=30m/s (along the perpendicular edge)
- V2x=20m/s (along one edge)
- V2y=20m/s (along the perpendicular edge)
To find the angle of motion for each ball, we can use the tangent function, which relates the opposite side to the adjacent side in a right triangle.
tan(α)=V1yV1x=3010√3=3010⋅1.732=3017.32≈1.732
Thus, α=tan−1(1.732). We know that tan(60∘)=√3, so:
α=60∘
tan(β)=V2yV2x=2020=1
Thus, β=tan−1(1). We know that tan(45∘)=1, so:
β=45∘
The angle θ between the two directions of motion is given by:
θ=α−β=60∘−45∘=15∘
The angle between the directions of motion of the two balls is 15∘.
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - EXERCISE-5(A)15videos
MISCELLANEOUS
- BOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Exersice -05(B)19videos
MISCELLANEOUS
- BOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Exercise-04 [A]28videos
MISCELLANEOUS
- BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-78videos
KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)
- BOOK - ALLENCHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-IV8videos
PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT
Similar Questions
The components of a particles velocity in the directions at right angles are 3m/s,4m/sand 12m/s respectively . The actual velocity of the particle , in m/s is
View SolutionTwo elastic bodies P and Q having equal mases are moving along the same line with velocities of 16 m/s and 10 m/s respectively. Their velocities after the elastic collision will be in m/s :
View SolutionA harmonically moving transverse wave on a string has a maximum particle velocity and acceleration of 3 m/s and 90m/s2 respectively. Velocity of the wave is 20m/s. Find the waveform.
View SolutionTwo particles are projected from a tower horizontally in opposite directions with velocities 10m/sand20m/s. Find the time when their velocity vectors are mutually perpendicular. Take g=10m/s2.
View SolutionTwo equal masses m1 and m2 moving along the same straight line with velocites +3m/s and −5m/s respectively collide elastically. Their velocities after the collision will be respectively.
View SolutionTwo equal masses m1 and m2 moving along the same straight line with velocites +3m/s and −5m/s respectively collide elastically. Their velocities after the collision will be respectively.
View SolutionTwo objects of masses 100g and 200g are moving along the same line in the same direction with velocities of 2m/s and 1m/s, respectively. They collide and after the collison, the first object moves at a velocity of 1.67m/s in the same direction. Determine the velocity of the second object.
View SolutionTwo rings of radii 5m and 10m move in opposite directions with velocity 20 m/s and 10 m/s respectively, on a conducting curface S. There is a uniform magnetic field of magnitude 0.1T perpendicular to the plane of the rings. Find the potential difference between the highest points of the two rings.
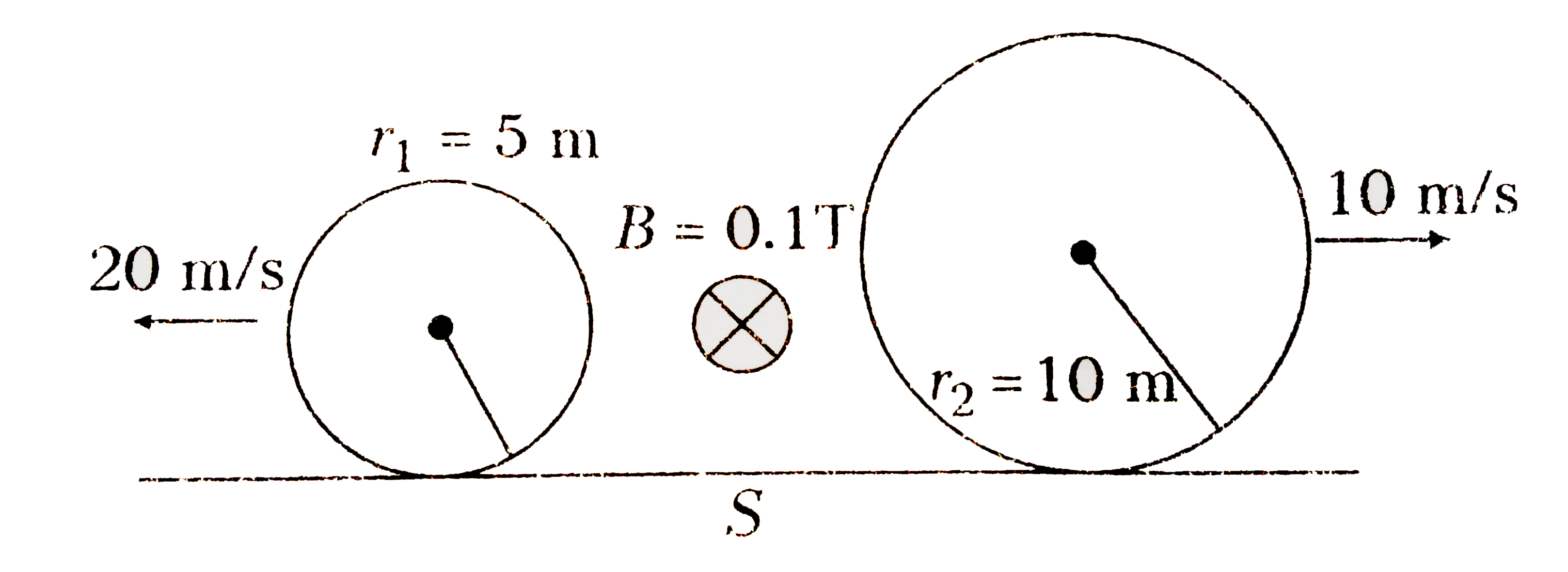 View Solution
View SolutionA stone is projected from level ground at t=0 sec such that its horizontal and vertical components of initial velocity are 10ms and 20ms respectively. Then the instant of time at which tangential and normal components of acceleration of stone are same is: (neglect air resistance)g=10ms2.
View SolutionA stone is projected from level ground at t=0 sec such that its horizontal and vertical components of initial velocity are 10ms and 20ms respectively. Then the instant of time at which tangential and normal components of acceleration of stone are same is: (neglect air resistance)g=10ms2.
View Solution

