The dimensions of 12ε0E2(ε0= permittivity of free space, E= electric field) is
[MLT−1]
[ML2T−2]
[ML−1T−2]
[ML2T−1]
The correct Answer is:C
12∈0E2−[M−1L−3T4I2][M2L2T−6I−2]=[M1L−1T−2]
Topper's Solved these Questions
- MISCELLANEOUSBook:ALLENChapter:MISCELLANEOUSExercise:Exercise-02
Explore 77 Videos
- MISCELLANEOUSBook:ALLENChapter:MISCELLANEOUSExercise:Exercise-03
Explore 1 Video
- MISCELLANEOUSBook:ALLENChapter:MISCELLANEOUSExercise:EXERCISE-5(A)
Explore 15 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)Book:ALLENChapter:KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)Exercise:BEGINNER S BOX-7
Explore 8 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT Book:ALLENChapter:PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT Exercise:EXERCISE-IV
Explore 8 Videos
Similar Questions
A ladder, 5 maters long, standing on a horizontal floor, leans against a vertical wall. If the top of the ladder slides downwards at the rate of 10 cm/sec, then find the rate at which the angle between the floor and the ladder is decreasing when lower end of the ladder is 2 meters away from the wall.
View SolutionTwo parallel metallic plates have surface charge densities σ1 and σ2 as shown in figure.
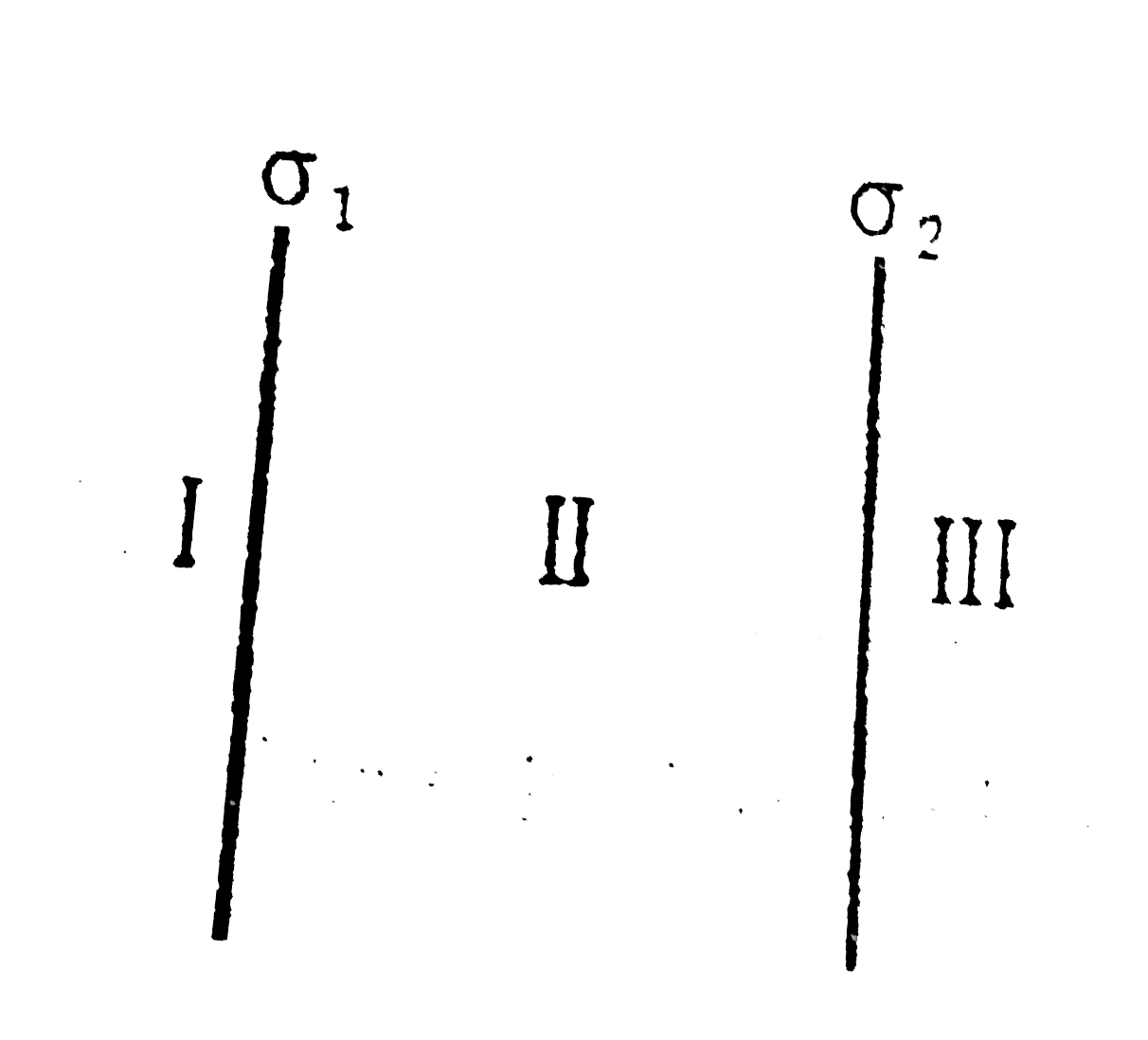
Column-IColumn-II(A)If σ1+σ2=0(p)Electric field in region III is towards right(B)Ifσ1+σ2>0(q)Electric field in region I is zero(C)If σ1+σ2<0(r)Electric field in region I is towards roght(s)Nothing can be said
View SolutionIdentify the pair whose dimensions are equal.
View SolutionA football player kicks a ball at an angle of 30∘ with an initial speed of 20 m/s. Assuming that the ball travel in a vertical plane, calculate
the time for which the ball is in the air. (g=10 m/s2)
View SolutionAssertion : Gravitational forces do not depend on the medium between the masses.
Reason : Mediating particle responsible for gravitational force is graviton.
View SolutionThe dimension of (12)ε0E2 (ε0 : permittivity of free space, E electric field
View SolutionThe dimensions of 12ε0E2(ε0= permittivity of free space, E= electric field) is
View SolutionThe dimensions of 12ε0E2(ε0= permittivity of free space, E= electric field) is
View Solutionepsilon_(0)E^(2) has the dimensions of ( epsilon_(0)= permittivity of free space, E= electric field) Here k= Boltzmann consant T= absolute temperature R= universal gas constant.
View Solution12ε0E2 की विमा लिखिए (जहाँ ε0 मुक्त स्थाक की वैघुतशीलता तथा E वैघुत क्षेत्र की तीव्रता हैं।
View SolutionThe dimensions of 12∈0E2, where ∈0 is permittivity of free space and E is electric field, is :-
View SolutionThe dimensions of (1)/(2)epsilon_(0)E^(2) (epsilon_(0)= permitivity of free space and E = electric field) are :
View SolutionThe dimension of (1)/(2) epsilon_(0)E^(2) . Where epsilon_(0) is permittivity of free space and E is electric field is
View Solutionμ0 and ε0 denote the permeability and permittivity of free space, the dimensions of μ0ε0 are
View SolutionThe dimensions of 12εE2. Where ε0 is permittivity of free space and E is electric field is
View SolutionThe dimension of ( 1 2 ) ε 0 E 2(permittivity of free space: E : electric field) is :-
View Solution