Two charges abd are located at the points with coordinates and respectively in the x-y plane. (i) Show that all points in the x-y plane where the electric potential due to the charges is zero, on a circle. Find its radius and the location of its centre (ii) Give the expression V(x) at a general point on the x-axis and sketch the function V(x) on the whole x-axis. (iii) If a particle of charge +q starts from rest at the centre of the circle, shown by a short quantitative argument that the particle eventually crosses the circule. Find its speed when it does so.
The correct Answer is:(i) (ii) for for
(iii)
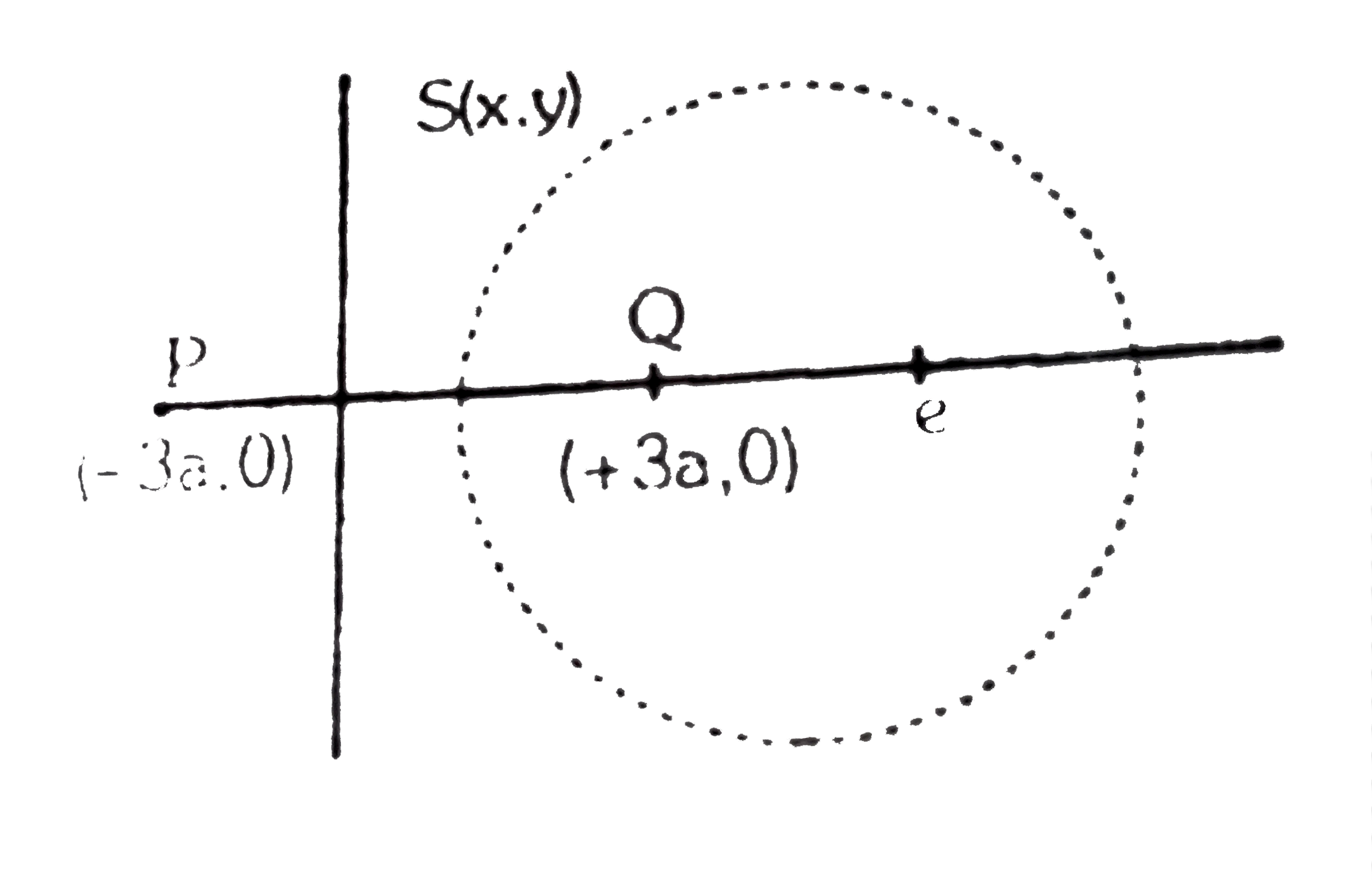
and radius
for
for
[C] A positive charge when released will move from high potential to low potential
COME:
Topper's Solved these Questions
- MISCELLANEOUSBook:ALLENChapter:MISCELLANEOUSExercise:Exersice-04[B]
Explore 16 Videos
- MISCELLANEOUSBook:ALLENChapter:MISCELLANEOUSExercise:Exercise-05(A)
Explore 35 Videos
- MISCELLANEOUSBook:ALLENChapter:MISCELLANEOUSExercise:Comprehension 9
Explore 2 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)Book:ALLENChapter:KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)Exercise:BEGINNER S BOX-7
Explore 8 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT Book:ALLENChapter:PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT Exercise:EXERCISE-IV
Explore 8 Videos
Similar Questions
Two fixed charges -2Q and Q are located at the point with coordinates (-3a,0) and (+3a,0) respectively in the x- y plane .
Show that all points in the x-y plane where the electric potential due to the two charge is zero , lie on a circle. If its radius is r = xa and the location of its centre is (ya,0) find x and y .
View SolutionTwo fixed charges -2Q and Q are located at the point with coordinates (-3a,0) and (+3a,0) respectively in the x- y plane .
Show that all points in the x-y plane where the electric potential due to the two charge is zero , lie on a circle. If its radius is r = xa and the location of its centre is (ya,0) find x and y .
View Solution
Knowledge Check
Two fixed charges −2Q and Q are locatted at the points with coordinates ( -3 a, 0) and (+3 a, 0) prespectively in the X−Y plane .
All the points in the X−Y plane where the electric potential due to the two charges is zero , line on a .Astraight lineBcircleCparabolaDellipseTwo fixed charges −2Q and Q are locatted at the points with coordinates ( -3 a, 0) and (+3 a, 0) prespectively in the X−Y plane .
The expression for the potential V(x) at a general point on the x-axis is given by .AV(x)=14πɛ0[Q3a−x−2Q(3a+x)]for0<x<3aBV(x)=14πɛ0[2Q3a−x−2Q(3a+x)]for0<x<3aCV(x)=14πɛ0[Q3a−x−2Q(3a+x)]for0<x<3aDV(x)=14πɛ0[Q3a−x−2Q(3a+x)]for0<x<3atwo point charges + 16 q and -4q located at x=0 and x=L respectively. the location of a point on the x-axis from x=0, at which the net electric field due to these two charges is zero is
ALB2LCL2DL4
Two fixed charges -2Q and Q are located at the point with coordinates (-3a,0) and (+3a,0) respectively in the x- y plane .
If a particle of charge +q starts from rest at the centre of the circle , show by a short quantitavtive argument that the particle eventually crosses the circle . If its speed V=√Qqzπε0ma , then find z.
View SolutionTwo fixed charges -2Q and Q are located at the point with coordinates (-3a,0) and (+3a,0) respectively in the x- y plane .
If a particle of charge +q starts from rest at the centre of the circle , show by a short quantitavtive argument that the particle eventually crosses the circle . If its speed V=√Qqzπε0ma , then find z.
View Solutiontwo point charges + 16 q and -4q located at x=0 and x=L respectively. the location of a point on the x-axis from x=0, at which the net electric field due to these two charges is zero is
View SolutionTwo point charges −q and +q are located at points (0,0−a) and (0,0,a) respectively. The electric potential at point (0,0,z)is (Z>a)
View SolutionTwo point charges +8q and -2q located at x =0 and x=L respectively . The location of a point on the x-axis at which the net electric field due to these two point charges is zero is.
View Solution
