A particle moved along the X−axis according to the graph shown in Figure. Choose the incorrct options.
The particle did not move in straight line from t=0s to t=5s.
The magnitude of displacement of particle from t=0s to t=5s is 2m.
The average speed of particle from t=0s to t=5s is 0.8m/s
The speed of particle is zero somewhere between t=3s to t=4s.
The correct Answer is:A
(1) since the particle is moving along x−axis it is straight line.
(2) s=xf−xi=2−0=2m
(3) distance =(3−0)+(3−2)=4
∴<V>.=45=0.8m/s
(4) Slope is zero between t=3 & 4sec
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - TEST PAPEREXERCISE - Exercise (Physics)330videos
TEST PAPER
- BOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS4videos
TEST PAPER
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example1videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - TEST PAPER 1EXERCISE - PHYSICS11videos
TEST PAPER 1
Similar Questions
A particle moves along the x-axis according to the equation x=asinωt+bcosωt. The motion is simple harmonic with
View SolutionFor a particle moving along x-axis, a scaled x-6 graph is shown in figure. Mark the correct statement (s).
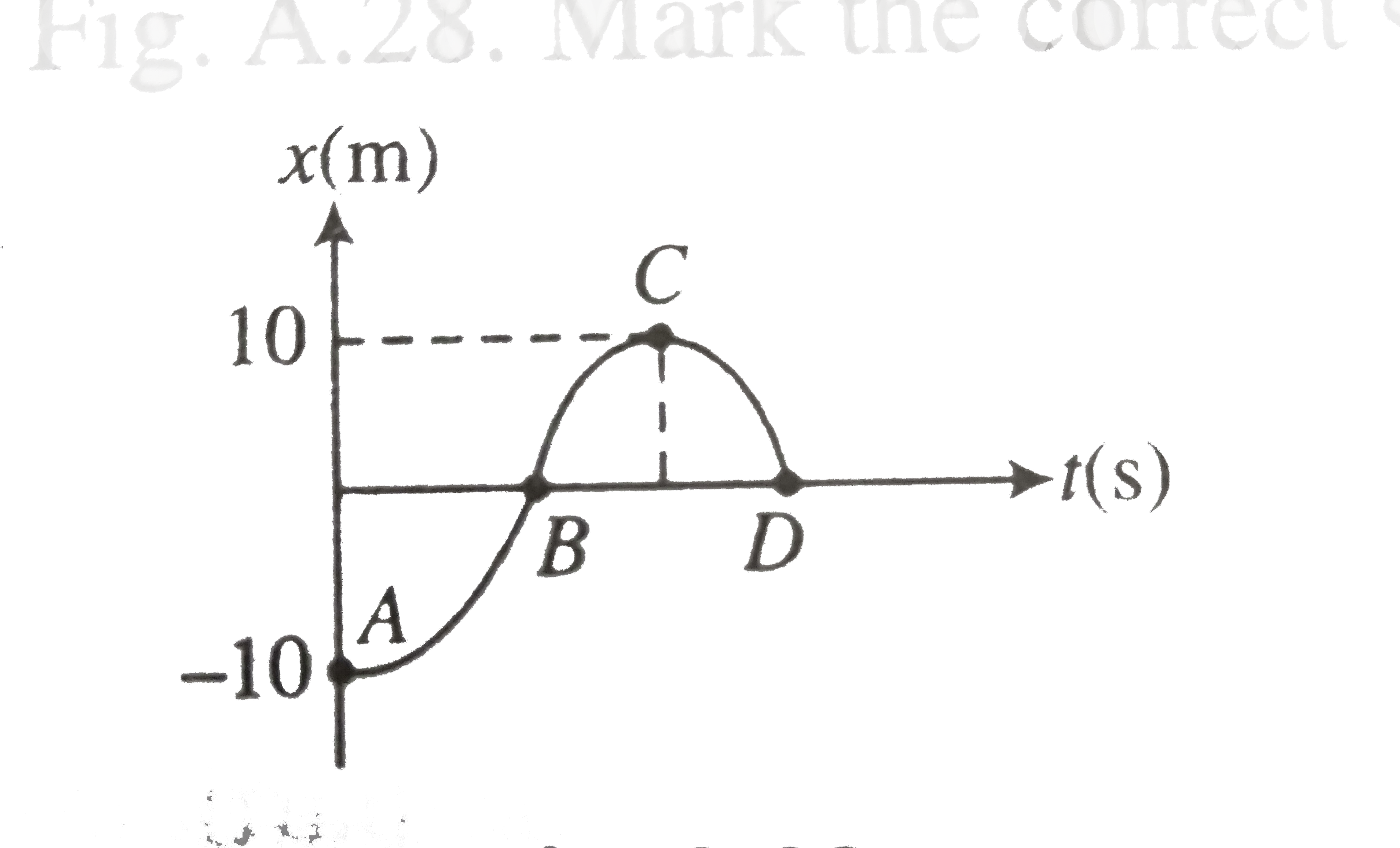
View SolutionThe velocity-time plot for a particle moving on a straight line is shown in figure. Choose correct options .
View SolutionFor a particle moving along the x-axis, x-t graph is as given as graph in figure. Mar the correct statement (s).
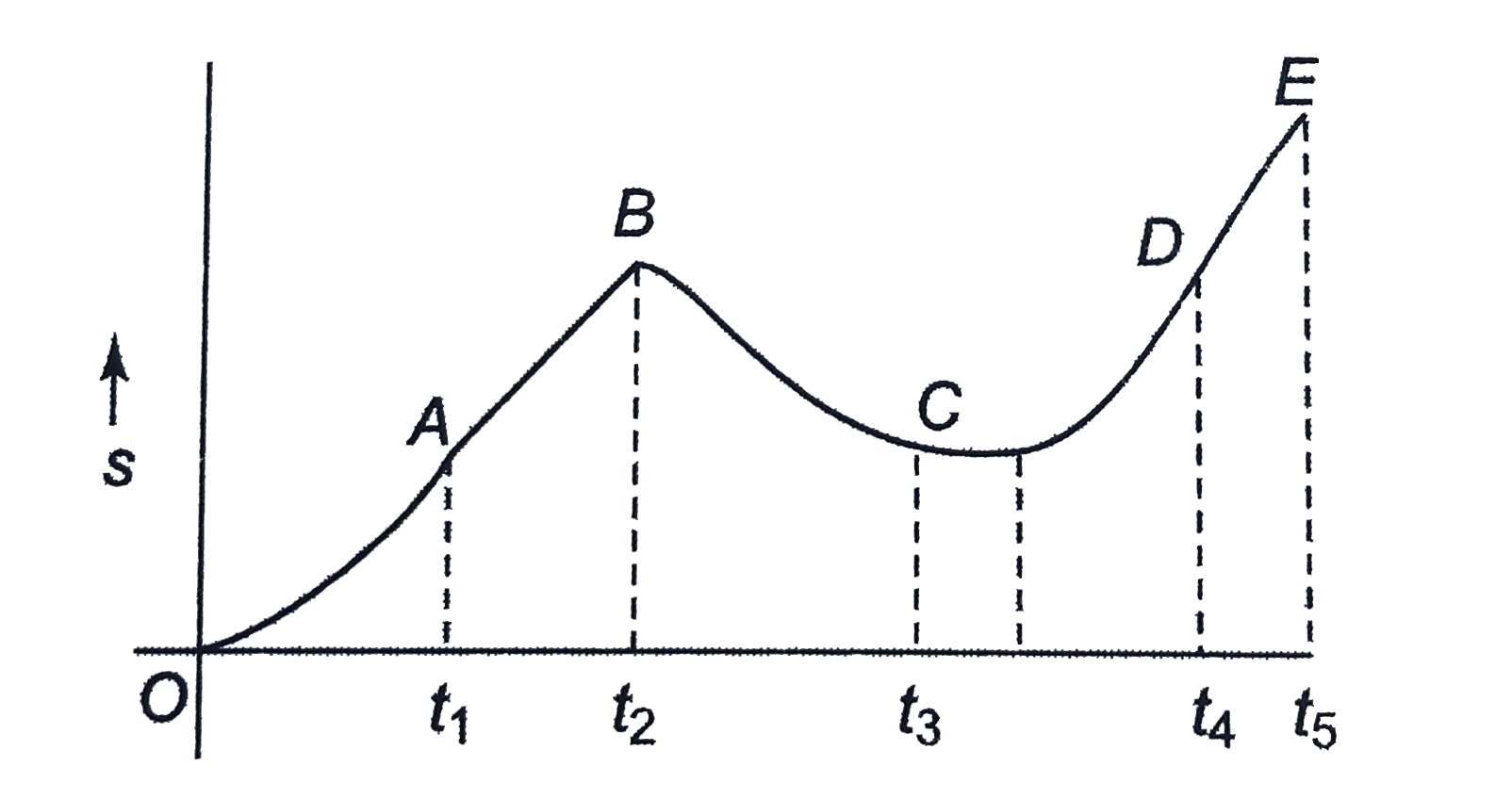
(#BMS_V01_MAA_E01_052_Q01.png" width="80%">View SolutionThe position (x) of a particle moving along x - axis veries with time (t) as shown in figure. The average acceleration of particle in time interval t = 0 to t = 8 s is
View SolutionThe magnitude of force acting on a particle moving along x-axis varies with time (t) as shown in figure. If at t = 0 the velocity of particle is v0, then its velocity at t=T0 will be
View SolutionA particle is moving along the x-axis and its position-time graph is shown. Determine the sign of acceleration.
View SolutionA particle moves along x-axis according to relation x=1+2sinωt. The amplitude of S.H.M. is
View SolutionThe velocity (υ) of a particle moving along X-axis varies with its position x as shown in figure. The acceleration (a) of particle varies with position (x) as
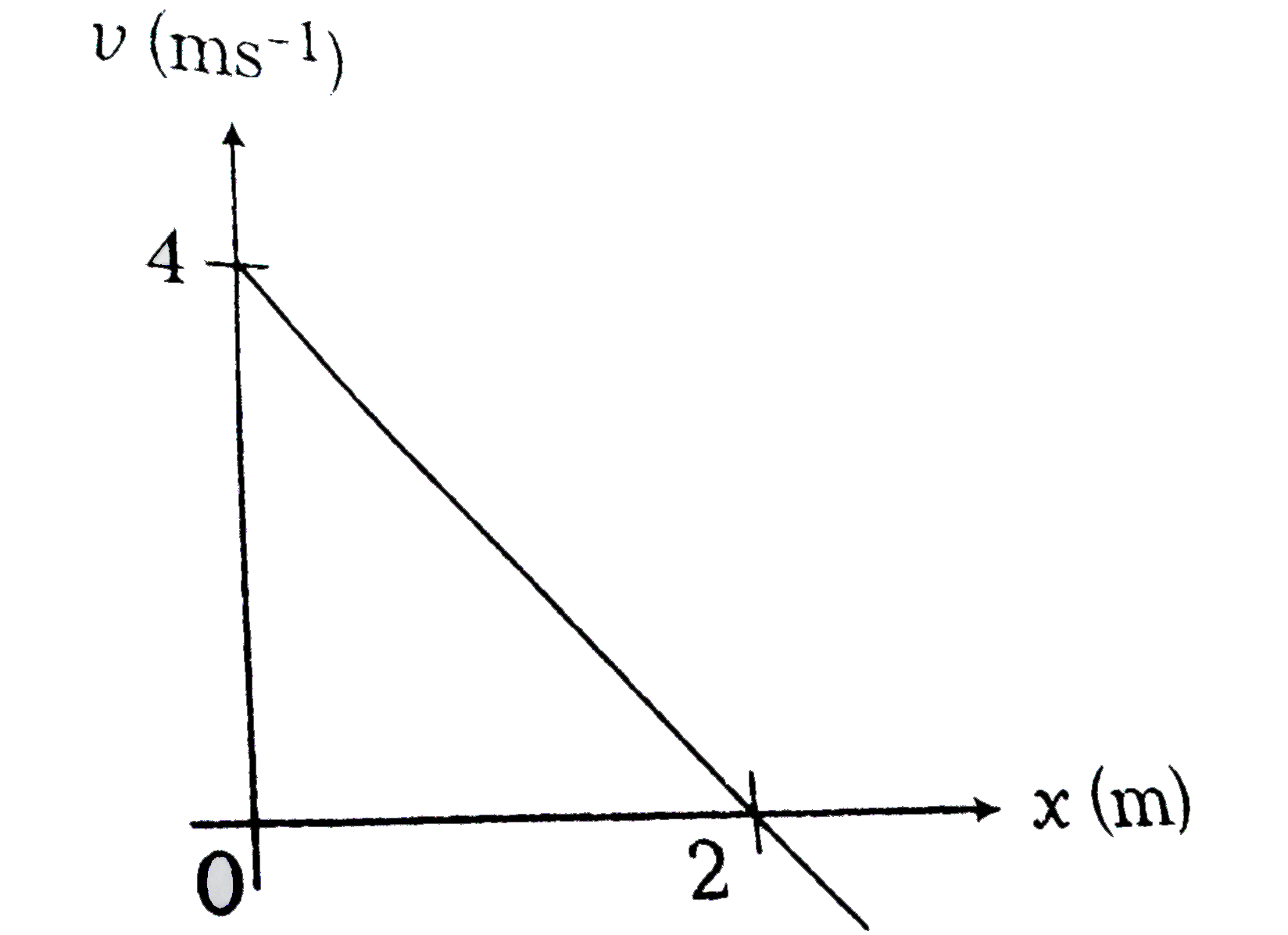
View SolutionThe acceleration-time (a−t) graph of a particle moving along straight line is as shown in figure. The time at which velocity of particle becomes equal to its initial velocity is
View Solution