For a particle moving along axis, speed must be increasing for the following graph
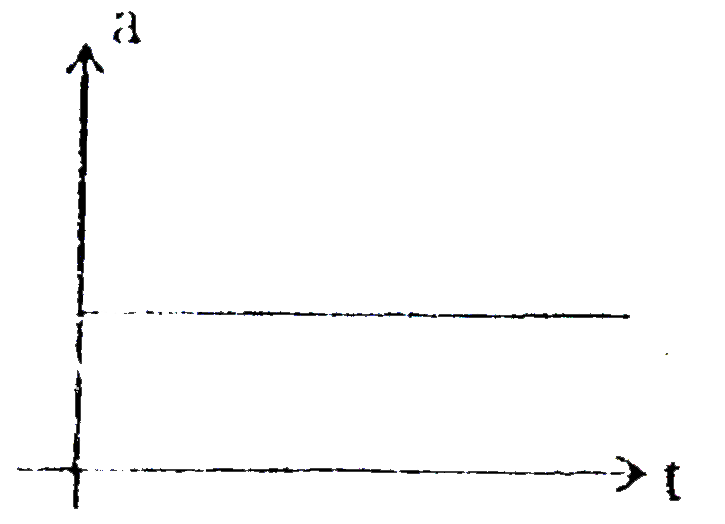
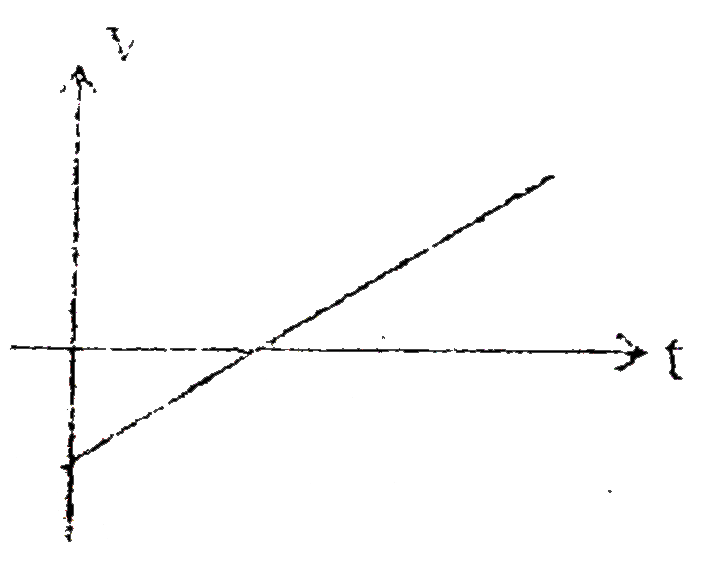
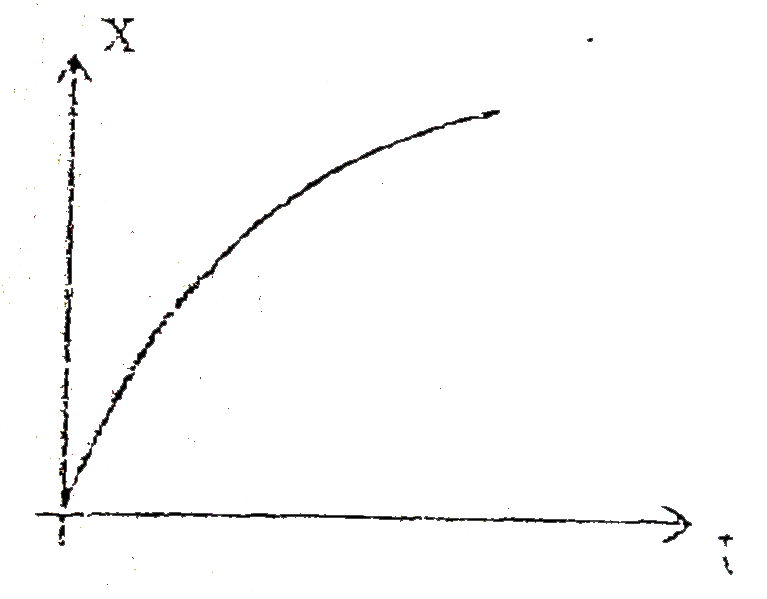
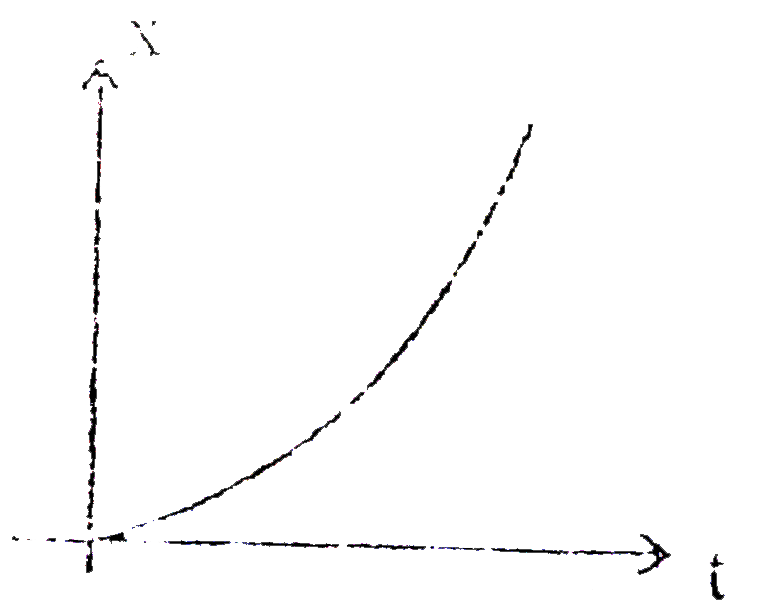
The correct Answer is:D
To determine when the speed of a particle moving along the x-axis is increasing, we need to analyze the relationship between velocity and acceleration. The speed of a particle increases when the velocity and acceleration have the same sign, meaning both are either positive or negative.
1. Understanding Speed and Velocity:
- Speed is the magnitude of velocity. For speed to increase, the particle must be moving in the same direction as its acceleration.
2. Identifying Conditions for Increasing Speed:
- Case 1: If the velocity is positive and the acceleration is also positive, the speed is increasing.
- Case 2: If the velocity is negative and the acceleration is also negative, the speed is also increasing.
3. Analyzing the Graph:
- Look at the graph provided. The slope of the graph represents the velocity of the particle.
- A positive slope indicates positive velocity, while a negative slope indicates negative velocity.
4. Determining the Slope:
- Identify sections of the graph where the slope is positive (indicating positive velocity) and where the slope is negative (indicating negative velocity).
- Check the acceleration (the slope of the velocity graph). If the slope is increasing (positive), the acceleration is positive.
5. Conclusion:
- The speed of the particle is increasing when both the velocity and acceleration are either positive or negative.
- From the analysis, if the graph shows sections where both the velocity and acceleration are positive or both are negative, then the speed is increasing.
Final Answer:
The correct answer is D, where the conditions for increasing speed are satisfied.
- Speed is the magnitude of velocity. For speed to increase, the particle must be moving in the same direction as its acceleration.
- Case 1: If the velocity is positive and the acceleration is also positive, the speed is increasing.
- Case 2: If the velocity is negative and the acceleration is also negative, the speed is also increasing.
- Look at the graph provided. The slope of the graph represents the velocity of the particle.
- A positive slope indicates positive velocity, while a negative slope indicates negative velocity.
- Identify sections of the graph where the slope is positive (indicating positive velocity) and where the slope is negative (indicating negative velocity).
- Check the acceleration (the slope of the velocity graph). If the slope is increasing (positive), the acceleration is positive.
- The speed of the particle is increasing when both the velocity and acceleration are either positive or negative.
- From the analysis, if the graph shows sections where both the velocity and acceleration are positive or both are negative, then the speed is increasing.
The correct answer is D, where the conditions for increasing speed are satisfied.
Topper's Solved these Questions
Similar Questions
The potential energy U(x) of a particle moving along x−axis is shown in figure. Which one of the following graphs represents the variation of kinetic energy of this particel if its total mechanical enery is E0
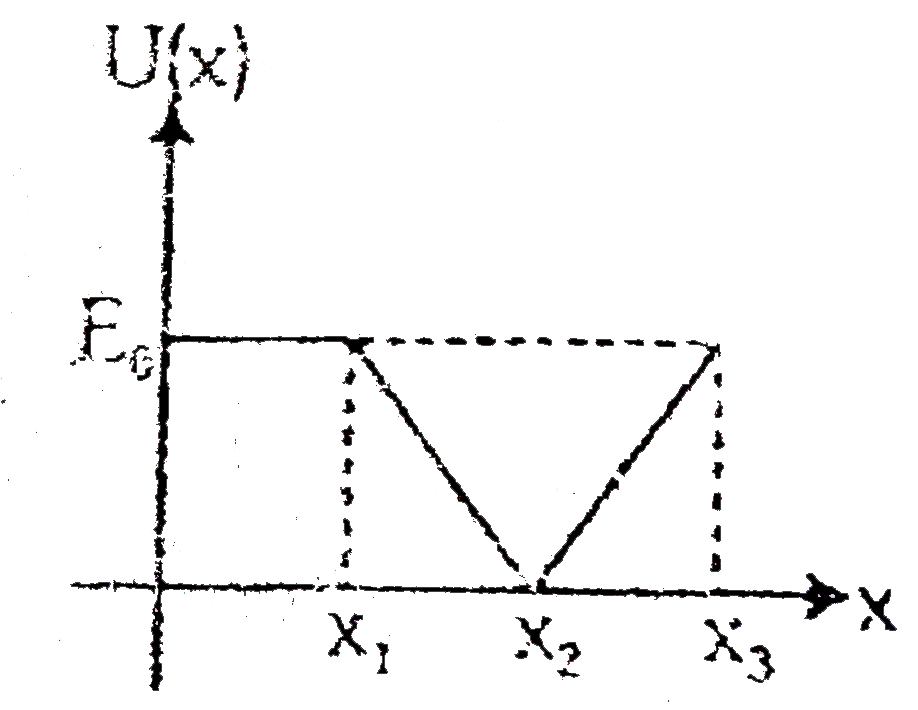 View Solution
View SolutionIf a particle is moving along straight line with increasing speed, then
View Solution
Knowledge Check
- Question 1 - Select One
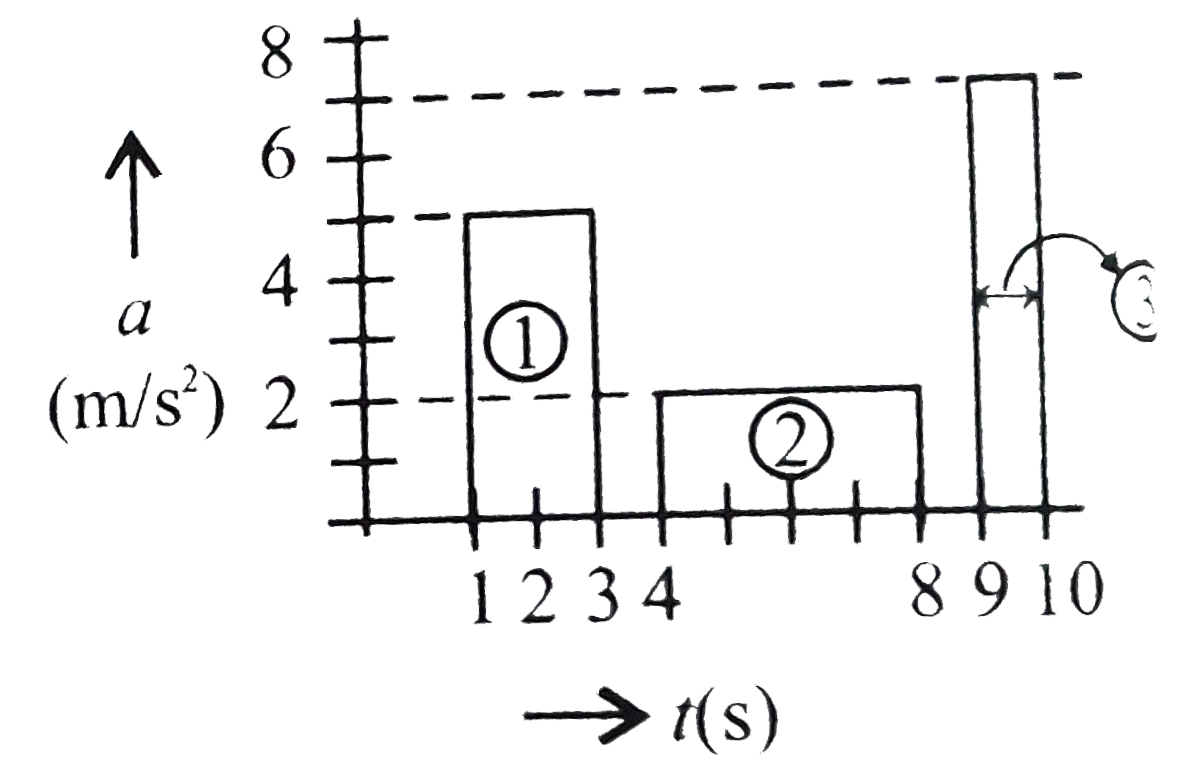
The figure shows a particle moving along x - axis subjected to three particles of acceleration (a). Rank the periods according to the increase they produce in the particle velocity, greatest first.
 A
A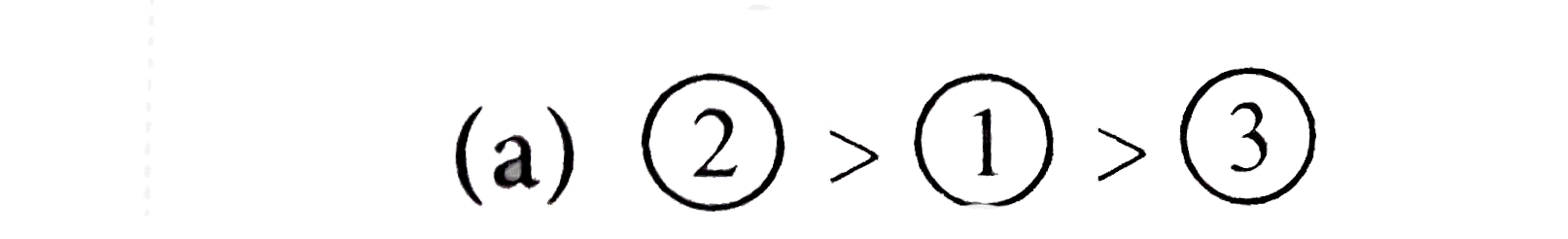 B
B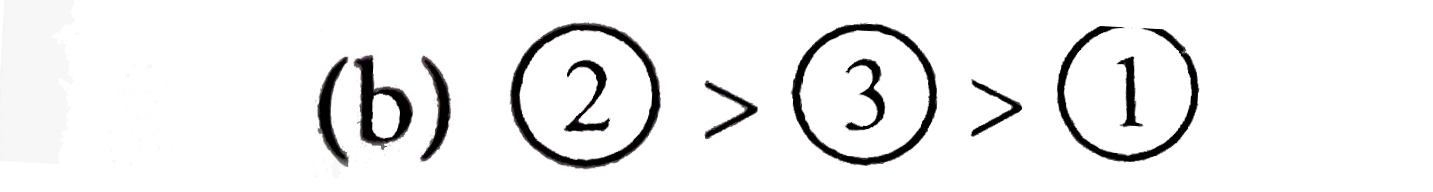 C
C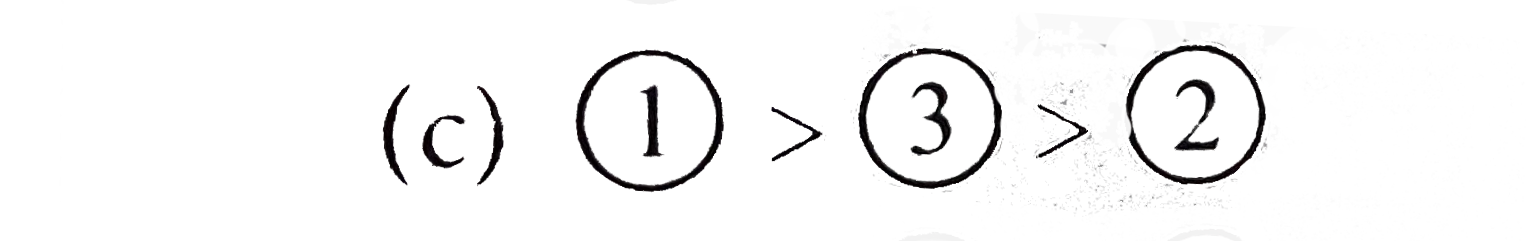 D
D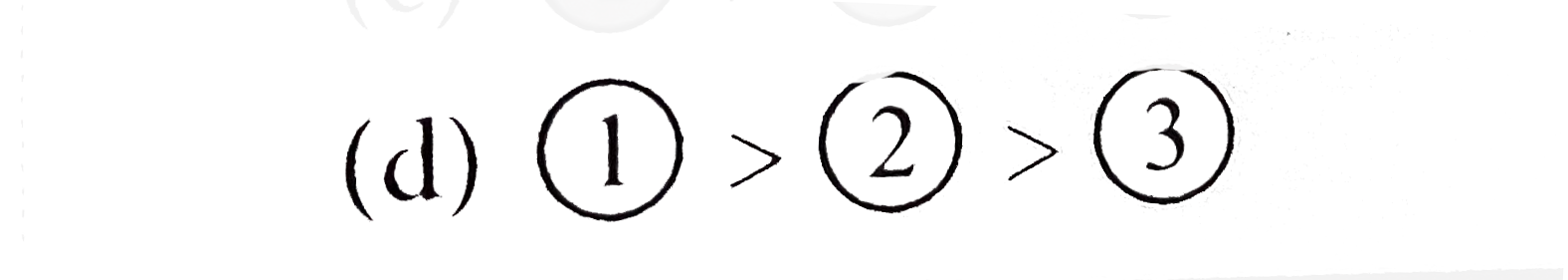
For a particle moving along the x-axis, mark the correct statement(s).
View SolutionThe velocity versus time graph of two particles moving along x-axis varies are shown in the following two plots. Then
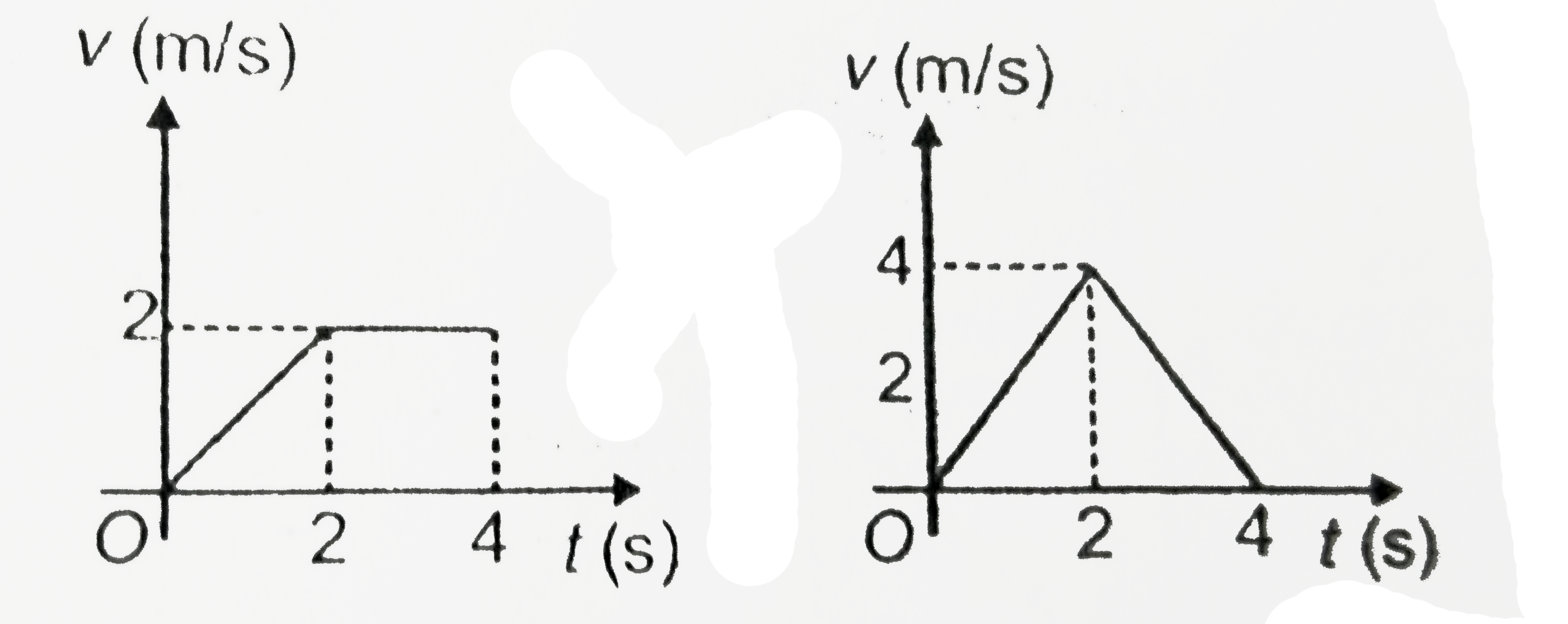 View Solution
View SolutionFor a particle moving along the x-axis, x-t graph is as given as graph in figure. Mar the correct statement (s).
(#BMS_V01_MAA_E01_052_Q01.png" width="80%">View SolutionFor a particle moving along x-axis, a scaled x-6 graph is shown in figure. Mark the correct statement (s).
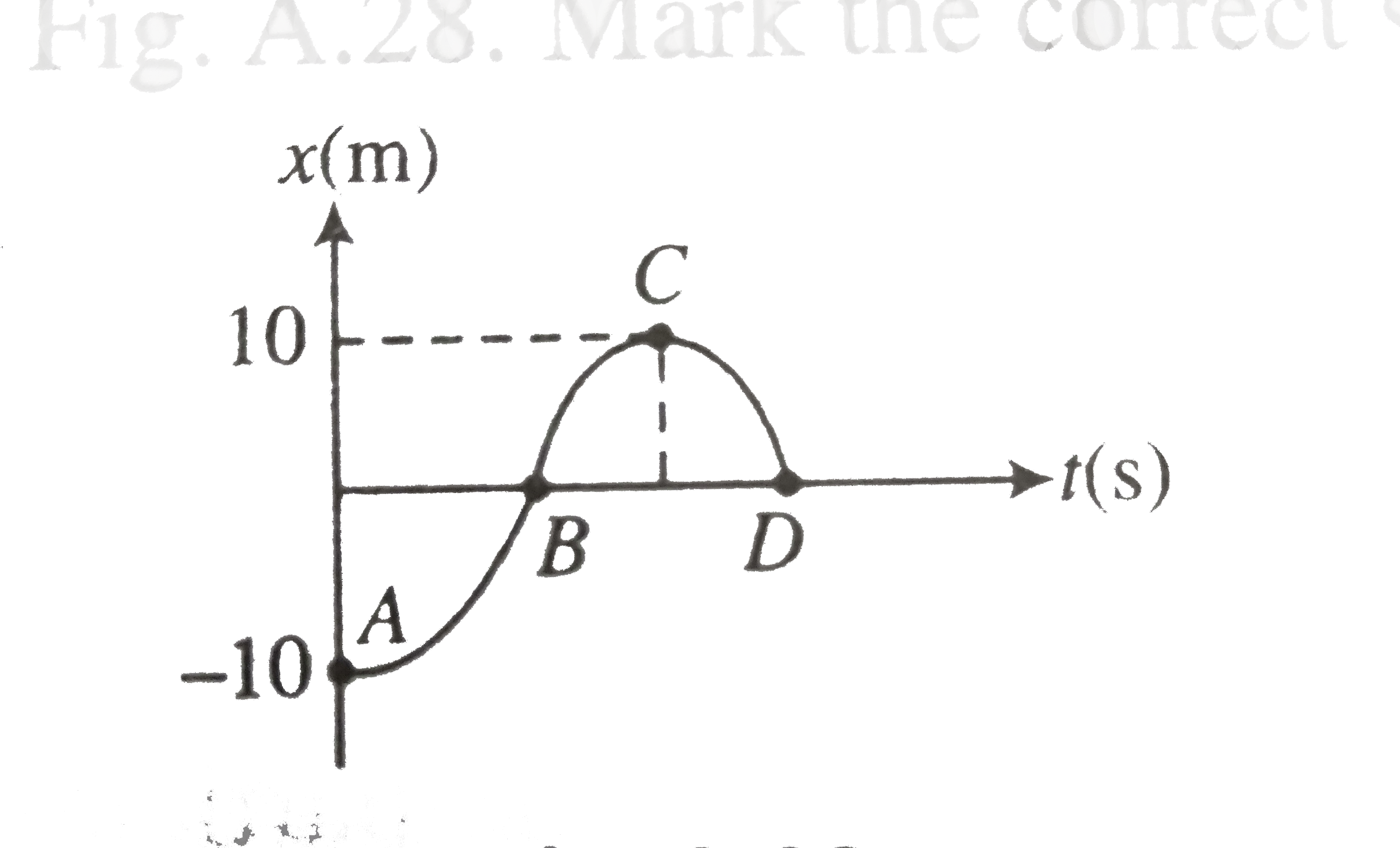 View Solution
View SolutionThe velocity (v) - time (t) graph for a particle moving along x - axis is shown in the figure. The corresponding position (x) - time (t) is best represented by
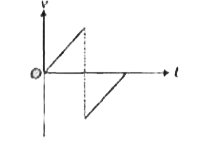 View Solution
View SolutionA particle moves along x-axis as x=4(t−2)+a(t−2)2
Which of the following is true?View SolutionThe acceleration - time graph for a particle moving along x - axis is shown in figure, If the initial velocity of particle is −5m/s, the velocity at t = 8 s is
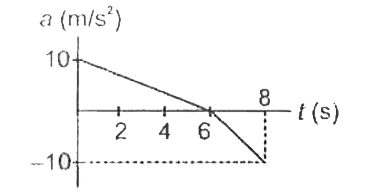 View Solution
View Solution

