The equation of one dimensional motion of the particle is described in column I. At t=0, particle is at origin and at rest. Match the column I with the statement in Column II.
Column IColumn II(A)x=(3t2+2)m(p)Velocity of particle at t=1s is 8m/s(B)v=8tm/s(q)Particle moves with uniform acceleration(C)a=16t(r)Particle moves with variable acceleration(D)v=6t−3t2(s)Particle will change its direction some time
The correct Answer is:(A)-q, (B)-p, q (C)-p, r, (D)-r, s
To solve the problem, we need to match the equations of motion provided in Column I with the corresponding statements in Column II. Let's analyze each equation step by step.
1. Analyze Column I - Part A:
- Given: x=3t2+2 m
- To find the velocity v, we differentiate x with respect to t:
v=dxdt=ddt(3t2+2)=6t m/s
- To find the acceleration a, we differentiate v with respect to t:
a=dvdt=ddt(6t)=6 m/s2
- Since the acceleration is constant, the particle moves with uniform acceleration. Thus, A matches with Q.
2. Analyze Column I - Part B:
- Given: v=8t m/s
- At t=1 s:
v=8×1=8 m/s
- The acceleration a is:
a=dvdt=8 m/s2
- Since the acceleration is constant, this indicates uniform acceleration. Thus, B matches with P and Q.
3. Analyze Column I - Part C:
- Given: a=16t m/s²
- Since acceleration depends on time, it is variable. Thus, C matches with R.
4. Analyze Column I - Part D:
- Given: v=6t−3t2
- To find acceleration:
a=dvdt=6−6t
- The acceleration is variable since it depends on t.
- To find when the particle changes direction, set v=0:
6t−3t2=0⟹3t(2−t)=0⟹t=0 or t=2
- The particle changes direction at t=2 s. Thus, D matches with S.
Final Matching:
- A matches with Q
- B matches with P and Q
- C matches with R
- D matches with S
Summary of Matches:
- A → Q
- B → P, Q
- C → R
- D → S
- Given: x=3t2+2 m
- To find the velocity v, we differentiate x with respect to t:
v=dxdt=ddt(3t2+2)=6t m/s
- To find the acceleration a, we differentiate v with respect to t:
a=dvdt=ddt(6t)=6 m/s2
- Since the acceleration is constant, the particle moves with uniform acceleration. Thus, A matches with Q.
- Given: v=8t m/s
- At t=1 s:
v=8×1=8 m/s
- The acceleration a is:
a=dvdt=8 m/s2
- Since the acceleration is constant, this indicates uniform acceleration. Thus, B matches with P and Q.
- Given: a=16t m/s²
- Since acceleration depends on time, it is variable. Thus, C matches with R.
- Given: v=6t−3t2
- To find acceleration:
a=dvdt=6−6t
- The acceleration is variable since it depends on t.
- To find when the particle changes direction, set v=0:
6t−3t2=0⟹3t(2−t)=0⟹t=0 or t=2
- The particle changes direction at t=2 s. Thus, D matches with S.
- A matches with Q
- B matches with P and Q
- C matches with R
- D matches with S
- A → Q
- B → P, Q
- C → R
- D → S
Topper's Solved these Questions
- KINEMATICSBOOK - ALLENCHAPTER - KINEMATICSEXERCISE - Assertion-Reason
20 Videos
- KINEMATICSBOOK - ALLENCHAPTER - KINEMATICSEXERCISE - Comprehension#1
3 Videos
- KINEMATICSBOOK - ALLENCHAPTER - KINEMATICSEXERCISE - EXERCISE-02
57 Videos
- ERROR AND MEASUREMENTBOOK - ALLENCHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)
22 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
Similar Questions
Starting from rest, the acceleration of a particle is a=2(t-1). The velocity of the particle at t=5s is :-
View SolutionMatch the following columns.
∣∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣∣Column IColumn II(A)d v/dt(p)Acceleration(B)d|v|/dt(q)Magnitude of acceleration(C)drdt(r)Velocity(D)∣∣drdt∣∣(s)Magnitude of velocity(t)Rate of change of speed∣∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣∣
View SolutionColumn II gives some equations. In these equations x is distance, t is time , m is mass, v is velocity u is initial velocity and F is force . Match the statements in Column I to the equations in Column II.
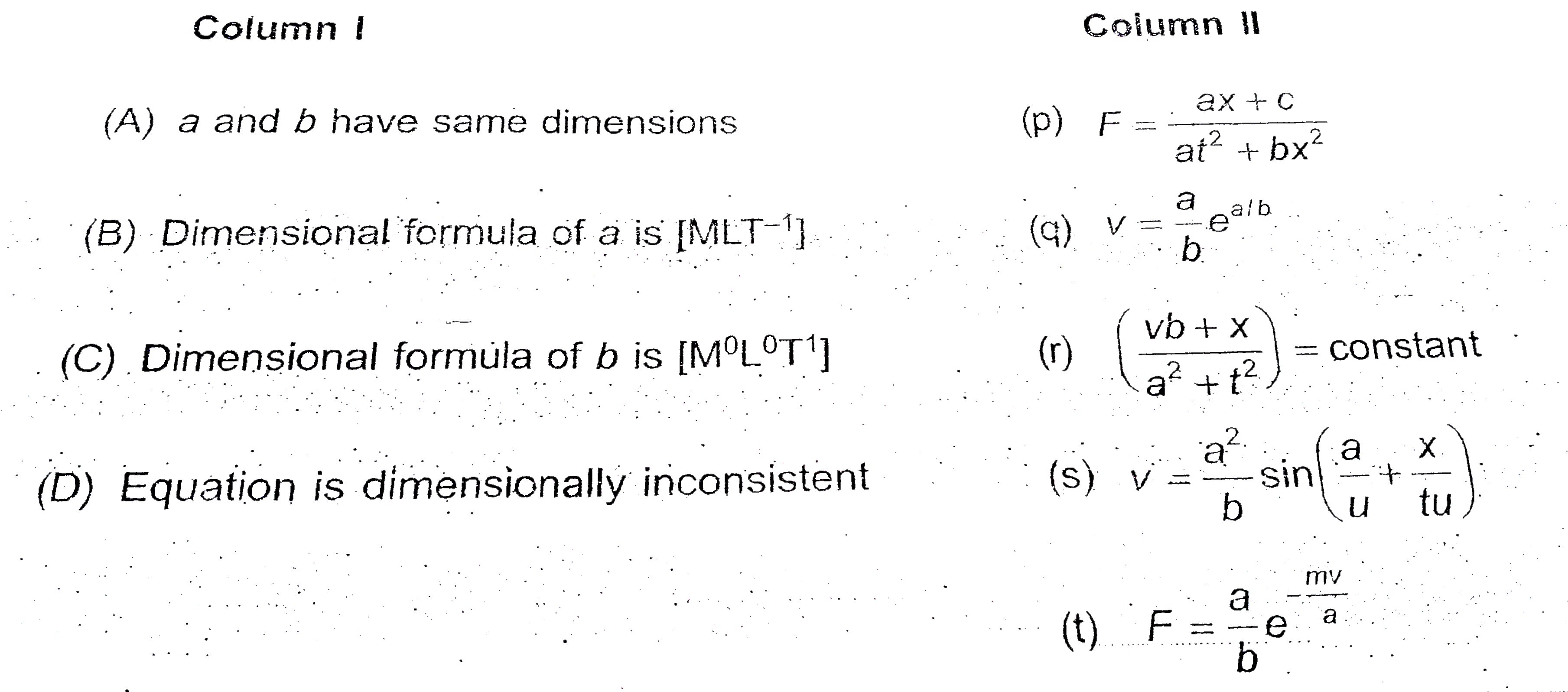
View SolutionThe acceleration a of a particle in ms2 is give by a=18t2+36t+120. If the particle starts from rest, then velocity at end of 1 s is
View SolutionA particle is moving with uniform acceleration. Its position (x) is given in terms of time (t in s) as X =(5t2+4t+8)m ,then
View SolutionVelocity of a particle is given as v=(2t2−3)m/s. The acceleration of particle at t = 3s will be :
View SolutionThe distance s of a particle in time t is given by s=t3−6t2−4t−8. Its acceleration vanishes at t=
View SolutionStarting from rest, the acceleration of a particle is a=2(t−1). The velocity (i.e.v=∫ a dt ) of the particle at t=10 s is :-
View SolutionThe motion of a particle along a straight line is described by the function x=(2t−3)2, where x is in metres and t is in seconds. Find
(a) the position, velocity and acceleration at t=2s.
(b) the velocity of the particle at origin.
View SolutionThe motion of a particle along a straight line is described by the function x=(2t−3)2, where x is in metres and t is in seconds. Find
(a) the position, velocity and acceleration at t=2s.
(b) the velocity of the particle at origin.
View Solution
