The value of vander waal's constant a and b for two gases X and
Y are 4.6,0.04 (for X) and 5.1, 0.06 (for Y). Which can be
liquified easily an appolication of pressure :-
X
Y
Both 1 & 2
None of these
The correct Answer is:A
To determine which gas, X or Y, can be liquefied more easily when pressure is applied, we will analyze the Van der Waals constants A and B for both gases.
1. Understand Van der Waals Constants:
- The Van der Waals constant a represents the strength of intermolecular forces. A lower value of a indicates weaker intermolecular forces, making it easier to liquefy the gas.
- The Van der Waals constant b represents the effective size of gas molecules. A lower value of b indicates that the molecules occupy less volume, which also facilitates liquefaction.
2. Given Values:
- For gas X:
- aX=4.6
- bX=0.04
- For gas Y:
- aY=5.1
- bY=0.06
3. Compare the Values of A:
- Compare aX and aY:
- aX(4.6)<aY(5.1)
- This indicates that gas X has weaker intermolecular forces compared to gas Y.
4. Compare the Values of B:
- Compare bX and bY:
- bX(0.04)<bY(0.06)
- This indicates that gas X occupies less volume per molecule compared to gas Y.
5. Conclusion:
- Since both aX<aY and bX<bY, gas X has both weaker intermolecular forces and a smaller effective size. Therefore, gas X can be liquefied more easily than gas Y when pressure is applied.
Final Answer:
Gas X can be liquefied more easily than gas Y.
- The Van der Waals constant a represents the strength of intermolecular forces. A lower value of a indicates weaker intermolecular forces, making it easier to liquefy the gas.
- The Van der Waals constant b represents the effective size of gas molecules. A lower value of b indicates that the molecules occupy less volume, which also facilitates liquefaction.
- For gas X:
- aX=4.6
- bX=0.04
- For gas Y:
- aY=5.1
- bY=0.06
- Compare aX and aY:
- aX(4.6)<aY(5.1)
- This indicates that gas X has weaker intermolecular forces compared to gas Y.
- Compare bX and bY:
- bX(0.04)<bY(0.06)
- This indicates that gas X occupies less volume per molecule compared to gas Y.
- Since both aX<aY and bX<bY, gas X has both weaker intermolecular forces and a smaller effective size. Therefore, gas X can be liquefied more easily than gas Y when pressure is applied.
Gas X can be liquefied more easily than gas Y.
Topper's Solved these Questions
- CHEMISTRY AT A GLANCEBOOK - ALLENCHAPTER - CHEMISTRY AT A GLANCEEXERCISE - INORGANIC CHEMISTRY
300 Videos
- CHEMISTRY AT A GLANCEBOOK - ALLENCHAPTER - CHEMISTRY AT A GLANCEEXERCISE - ORGANIC CHEMISTRY
472 Videos
- Chemical EquilibriumBOOK - ALLENCHAPTER - Chemical EquilibriumEXERCISE - All Questions
30 Videos
- ELECTROCHEMISTRYBOOK - ALLENCHAPTER - ELECTROCHEMISTRYEXERCISE - EXERCISE -05 [B]
38 Videos
Similar Questions

The table indicates the value of vander Waal's constant a in L2 atm mol−2. The gas which can most easily be liquefied is ?
View SolutionWhich of the following are correct statements ?
X) Vander Waal's constant a is a measure of attractive force
Y) Vander Waal's constant b is also called co-volume or excluded volume
Z) b is expressed in L mol−1
View Solution
Knowledge Check
If A and B are two events such that P(A) =0.2 , P(B) = 0.4 and P(A∪B)=0.6 then P(A/B) is equal to
A0B0.5C0.3D0.8
The following are the Vander Waal's parameters for four gases W, X, Y and Z
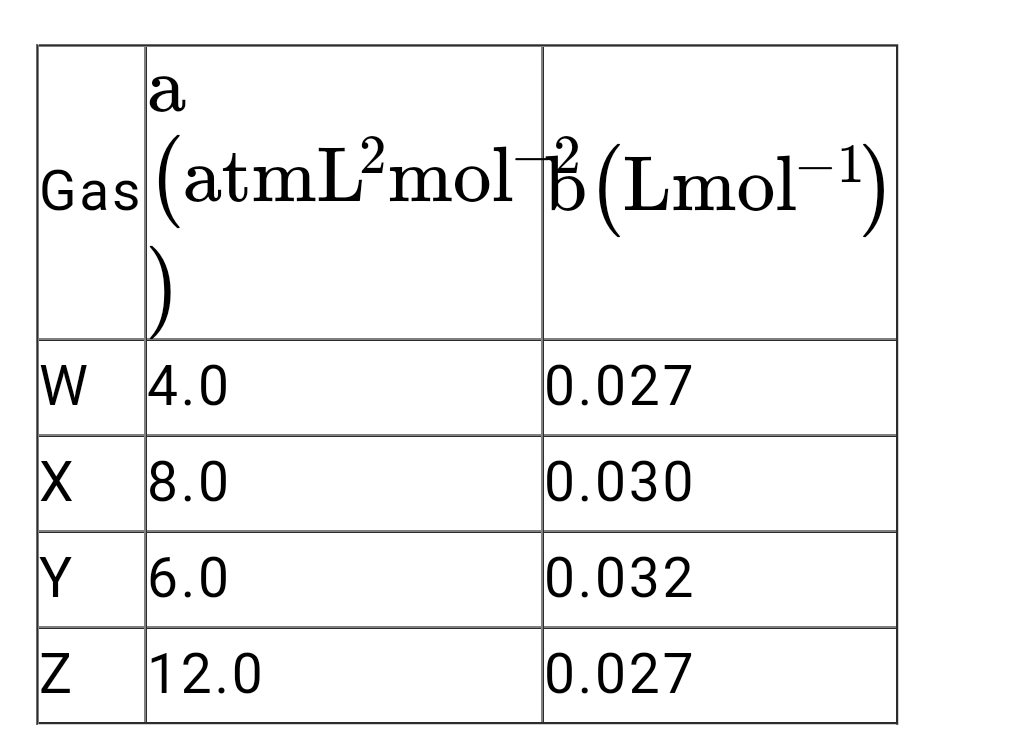
Based on given values identify, which one of these gases has highest critical temperature
View SolutionFind matrices X and Y , if X+Y=[5209] and X−Y=[360−1] .
View SolutionFind the value of x and y in given equations x+2y+3=0and4x−5y+1=0 .
View SolutionSeverely undernourished component of human population is
(a) 0.2
(b) 0.4
(c) 0.5
(d) 0.6
View SolutionA and B are two events such that P(A)=0.5,P(B)=0.4 and (AorB)=0.6, then find P(AandB).
View SolutionThe values of critical pressure (Pc) and critical temperature (Tc) for O2,Cl2,H2 and He are given below. The gas which has smallest value of Vander Waal's constant b'is

View SolutionIf the regrassion coefficient of Y on X is 1.6 that of X on Y is 0.4 , and θ be the angle between two regression lines , find the value of tanθ
View Solution
