For graphite which is possible ?
a=b=c,α=β=γ=90∘
a=b≠c,α=β=γ=90∘
a=b≠c,α=β=90∘,γ=120∘
a≠b≠c,α=β=γ=90∘
The correct Answer is:C
To answer the question "For graphite which is possible?", we will analyze the structure of graphite in terms of its unit cell and lattice parameters.
1. Understanding Graphite Structure:
- Graphite is a form of carbon that has a layered structure. Each layer consists of carbon atoms arranged in a hexagonal lattice.
2. Identifying the Lattice Type:
- The lattice structure of graphite is classified as a hexagonal close-packed (HCP) lattice. This means that the arrangement of atoms in the unit cell is hexagonal.
3. Defining Unit Cell:
- A unit cell is the smallest repeating unit in a crystal lattice that reflects the symmetry and structure of the entire lattice. For graphite, the unit cell is hexagonal.
4. Lattice Parameters:
- In the case of graphite, the lattice parameters are defined as follows:
- Axial lengths: a=b≠c
- Axial angles: α=β=90∘ and γ=120∘
5. Conclusion:
- Based on the above analysis, the correct conditions for the lattice parameters of graphite are:
- a=b (the lengths of the sides of the hexagon are equal)
- c (the height of the hexagonal prism) is different from a and b
- Angles: α=β=90∘ and γ=120∘
Thus, the correct answer is that for graphite, the condition a=b≠c is possible, along with the specified angles.
- Graphite is a form of carbon that has a layered structure. Each layer consists of carbon atoms arranged in a hexagonal lattice.
- The lattice structure of graphite is classified as a hexagonal close-packed (HCP) lattice. This means that the arrangement of atoms in the unit cell is hexagonal.
- A unit cell is the smallest repeating unit in a crystal lattice that reflects the symmetry and structure of the entire lattice. For graphite, the unit cell is hexagonal.
- In the case of graphite, the lattice parameters are defined as follows:
- Axial lengths: a=b≠c
- Axial angles: α=β=90∘ and γ=120∘
- Based on the above analysis, the correct conditions for the lattice parameters of graphite are:
- a=b (the lengths of the sides of the hexagon are equal)
- c (the height of the hexagonal prism) is different from a and b
- Angles: α=β=90∘ and γ=120∘
Topper's Solved these Questions
- CHEMISTRY AT A GLANCEBOOK - ALLENCHAPTER - CHEMISTRY AT A GLANCEEXERCISE - INORGANIC CHEMISTRY
300 Videos
- CHEMISTRY AT A GLANCEBOOK - ALLENCHAPTER - CHEMISTRY AT A GLANCEEXERCISE - ORGANIC CHEMISTRY
472 Videos
- Chemical EquilibriumBOOK - ALLENCHAPTER - Chemical EquilibriumEXERCISE - All Questions
30 Videos
- ELECTROCHEMISTRYBOOK - ALLENCHAPTER - ELECTROCHEMISTRYEXERCISE - EXERCISE -05 [B]
38 Videos
Similar Questions
Knowledge Check
Which of the following reaction is possible ?
AC6H5OH+HBr→C6H5Br+H2OB(CH3)3CCl+NaOCH3→(CH3)3COCH3+NaClC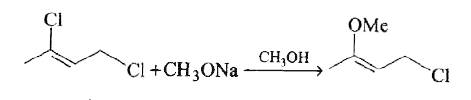 D
D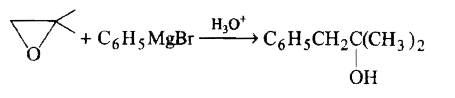
Which of the following reaction is possible ?
AC6H5OH+HBr→C6H5Br+H2OB(CH3)3CCl+NaOCH3→(CH3)3COCH3+NaClC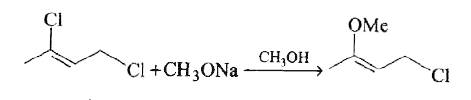 D
D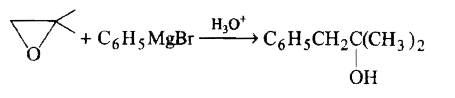
Which of the following reaction is possible ?
AC6H5OH+HBr→C6H5Br+H2OB(CH3)3CCl+NaOCH3→(CH3)3COCH3+NaClC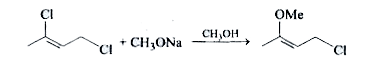 D
D
Among diamond and graphite, which is a good conductor of electricity ?
View SolutionGraphite is used as anode but diamond is not.
There exist free electrons between two parallel sheets of graphite, hence it helps in electrode conduction.
View SolutionOn the basis of enthalpy of formation, graphite is more stable than diamond, yet diamond does not change into graphite for years. Why ?
View SolutionWhich of the following is possible in ΔABC?
View SolutionWhich of the following reaction is possible ?
View Solution
