Geometrical isomers :
Structural isomers
Conformational isomers
Configurational isomers
None of these
The correct Answer is:C
Step-by-Step Text Solution:
1. Understanding Geometrical Isomers:
Geometrical isomers are a type of stereoisomer that arise due to restricted rotation around a double bond or a ring structure. They have the same molecular formula and the same structural formula but differ in the spatial arrangement of atoms or groups.
2. Identifying the Cause of Geometrical Isomerism:
The key factor that leads to geometrical isomerism is the presence of a double bond (C=C) or a cyclic structure, which restricts the rotation of the atoms or groups attached to the carbon atoms involved in the double bond or the ring.
3. Examples of Geometrical Isomers:
A classic example of geometrical isomers can be seen in compounds like 2-butene. In 2-butene, the two isomers are:
- Cis-2-butene: Both methyl groups (–CH₃) are on the same side of the double bond.
- Trans-2-butene: The methyl groups are on opposite sides of the double bond.
4. Classification of Isomerism:
Geometrical isomerism falls under the broader category of configurational isomerism. Isomerism can be classified into two main types:
- Structural Isomerism: Where the connectivity of atoms differs.
- Stereoisomerism: Where the connectivity is the same, but the spatial arrangement differs.
5. Types of Stereoisomerism:
Stereoisomerism can be further divided into:
- Configurational Isomerism: Where isomers cannot be interconverted without breaking bonds (e.g., geometrical and optical isomers).
- Conformational Isomerism: Where isomers can interconvert freely by rotation around single bonds.
6. Conclusion:
Therefore, geometrical isomers are specifically classified as a type of configurational isomerism due to the restricted rotation around double bonds or rings, leading to different spatial arrangements of atoms or groups.
---
Geometrical isomers are a type of stereoisomer that arise due to restricted rotation around a double bond or a ring structure. They have the same molecular formula and the same structural formula but differ in the spatial arrangement of atoms or groups.
The key factor that leads to geometrical isomerism is the presence of a double bond (C=C) or a cyclic structure, which restricts the rotation of the atoms or groups attached to the carbon atoms involved in the double bond or the ring.
A classic example of geometrical isomers can be seen in compounds like 2-butene. In 2-butene, the two isomers are:
- Cis-2-butene: Both methyl groups (–CH₃) are on the same side of the double bond.
- Trans-2-butene: The methyl groups are on opposite sides of the double bond.
Geometrical isomerism falls under the broader category of configurational isomerism. Isomerism can be classified into two main types:
- Structural Isomerism: Where the connectivity of atoms differs.
- Stereoisomerism: Where the connectivity is the same, but the spatial arrangement differs.
Stereoisomerism can be further divided into:
- Configurational Isomerism: Where isomers cannot be interconverted without breaking bonds (e.g., geometrical and optical isomers).
- Conformational Isomerism: Where isomers can interconvert freely by rotation around single bonds.
Therefore, geometrical isomers are specifically classified as a type of configurational isomerism due to the restricted rotation around double bonds or rings, leading to different spatial arrangements of atoms or groups.
Topper's Solved these Questions
Similar Questions
Knowledge Check
CH3=CH=CH−CH=CH−CH3, total number of geometrical isomer is :
A2B3C4D6Which of the following compounds does not have any geometrical isomer?
A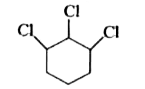 B
B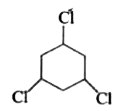 C
C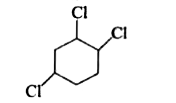 D
D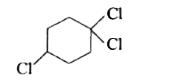
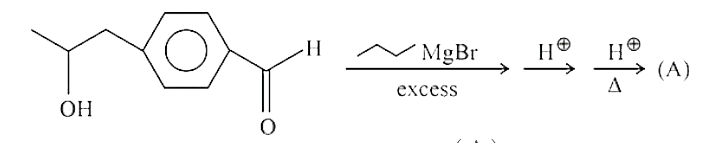
How many geometrical isomer of (A) is possible?
View SolutionGeometric isomers would be expected for which of the following compounds
View SolutionWhich of the following general properly of geometrical isomer is mis−match?
View SolutionWhich of the following is a pair of geometric isomers ?
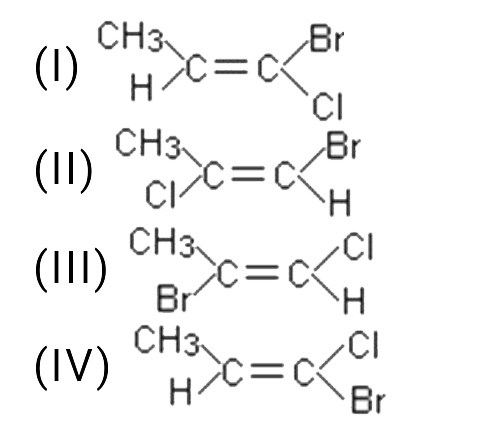
View SolutionWhich of the following compounds does not have any geometrical isomer?
View SolutionFor geometric isomers of 3–hexene :
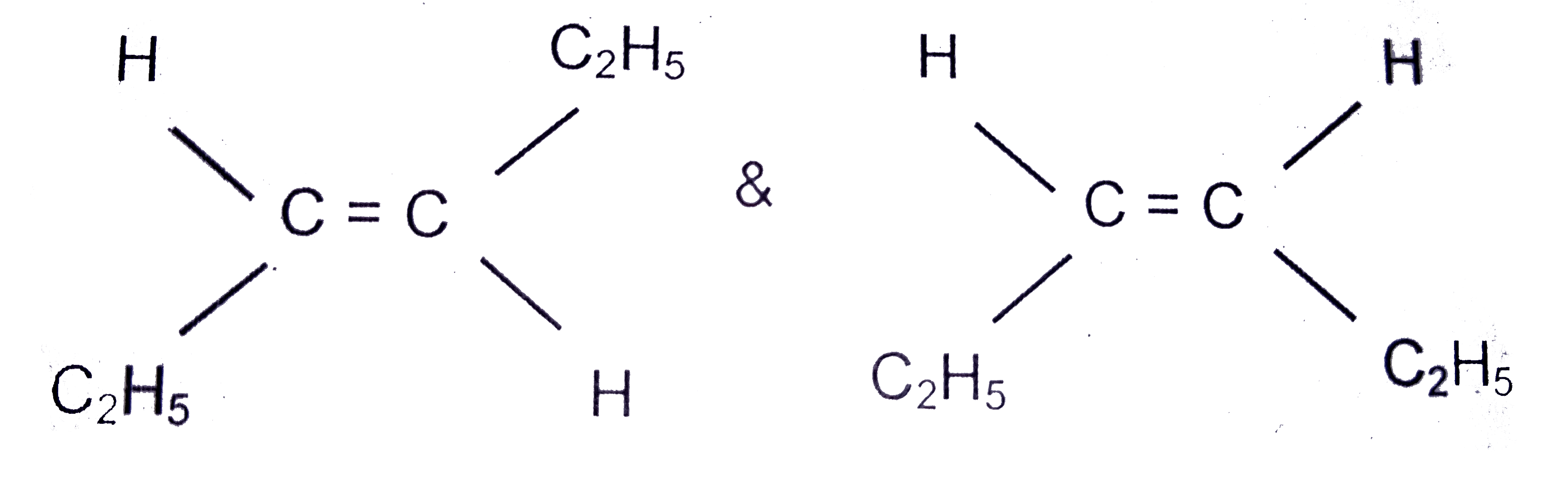
View Solution
