The internal energy of a system remains constant when it undergoes
(i) a cyclic process
(ii) an isothermal process
(iii) an adiabatic process
(iv) any process in which the heat given out by the system equal to the work done on the system
The correct Answer is:A, B, D
To determine when the internal energy of a system remains constant, we will analyze each of the given processes: cyclic, isothermal, adiabatic, and a specific process where the heat given out equals the work done on the system.
1. Cyclic Process:
- In a cyclic process, the system returns to its initial state after a series of changes.
- Since the internal energy depends only on the state of the system (temperature, pressure, volume), and the initial and final states are the same, the change in internal energy (ΔU) is zero.
- Conclusion: Internal energy remains constant. (Correct)
2. Isothermal Process:
- An isothermal process occurs at a constant temperature.
- Since temperature is constant, the change in temperature (ΔT) is zero.
- The change in internal energy (ΔU) is related to the change in temperature. Therefore, ΔU = nC_vΔT = 0.
- Conclusion: Internal energy remains constant. (Correct)
3. Adiabatic Process:
- In an adiabatic process, there is no heat exchange with the surroundings (Q = 0).
- According to the first law of thermodynamics: ΔU = Q - W.
- Since Q = 0, we have ΔU = -W. This indicates that any work done will change the internal energy.
- Conclusion: Internal energy does not remain constant. (Incorrect)
4. Any Process Where Heat Given Out Equals Work Done on the System:
- If the heat given out by the system equals the work done on the system, we can express this using the first law of thermodynamics: Q = ΔU + W.
- If the heat given out (Q) is negative (since it is rejected), and it equals the work done on the system (also negative), we can set Q = -W.
- Substituting this into the first law gives us: -W = ΔU + W. Rearranging gives ΔU = 0.
- Conclusion: Internal energy remains constant. (Correct)
Final Answer:
The internal energy of the system remains constant in the following processes:
- (i) Cyclic process
- (ii) Isothermal process
- (iv) Any process in which the heat given out by the system equals the work done on the system
Thus, the correct options are (i), (ii), and (iv).
---
- In a cyclic process, the system returns to its initial state after a series of changes.
- Since the internal energy depends only on the state of the system (temperature, pressure, volume), and the initial and final states are the same, the change in internal energy (ΔU) is zero.
- Conclusion: Internal energy remains constant. (Correct)
- An isothermal process occurs at a constant temperature.
- Since temperature is constant, the change in temperature (ΔT) is zero.
- The change in internal energy (ΔU) is related to the change in temperature. Therefore, ΔU = nC_vΔT = 0.
- Conclusion: Internal energy remains constant. (Correct)
- In an adiabatic process, there is no heat exchange with the surroundings (Q = 0).
- According to the first law of thermodynamics: ΔU = Q - W.
- Since Q = 0, we have ΔU = -W. This indicates that any work done will change the internal energy.
- Conclusion: Internal energy does not remain constant. (Incorrect)
- If the heat given out by the system equals the work done on the system, we can express this using the first law of thermodynamics: Q = ΔU + W.
- If the heat given out (Q) is negative (since it is rejected), and it equals the work done on the system (also negative), we can set Q = -W.
- Substituting this into the first law gives us: -W = ΔU + W. Rearranging gives ΔU = 0.
- Conclusion: Internal energy remains constant. (Correct)
The internal energy of the system remains constant in the following processes:
- (i) Cyclic process
- (ii) Isothermal process
- (iv) Any process in which the heat given out by the system equals the work done on the system
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -03
10 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - ASSERTION-REASON
36 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -01
65 Videos
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II
66 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
Similar Questions
Knowledge Check
The work done in adiabatic process is given by
AnR(T1)−T2γBnR(T1)−T2γ−1C(nR(T1)−T2)RDγ(T1)−T2Rn
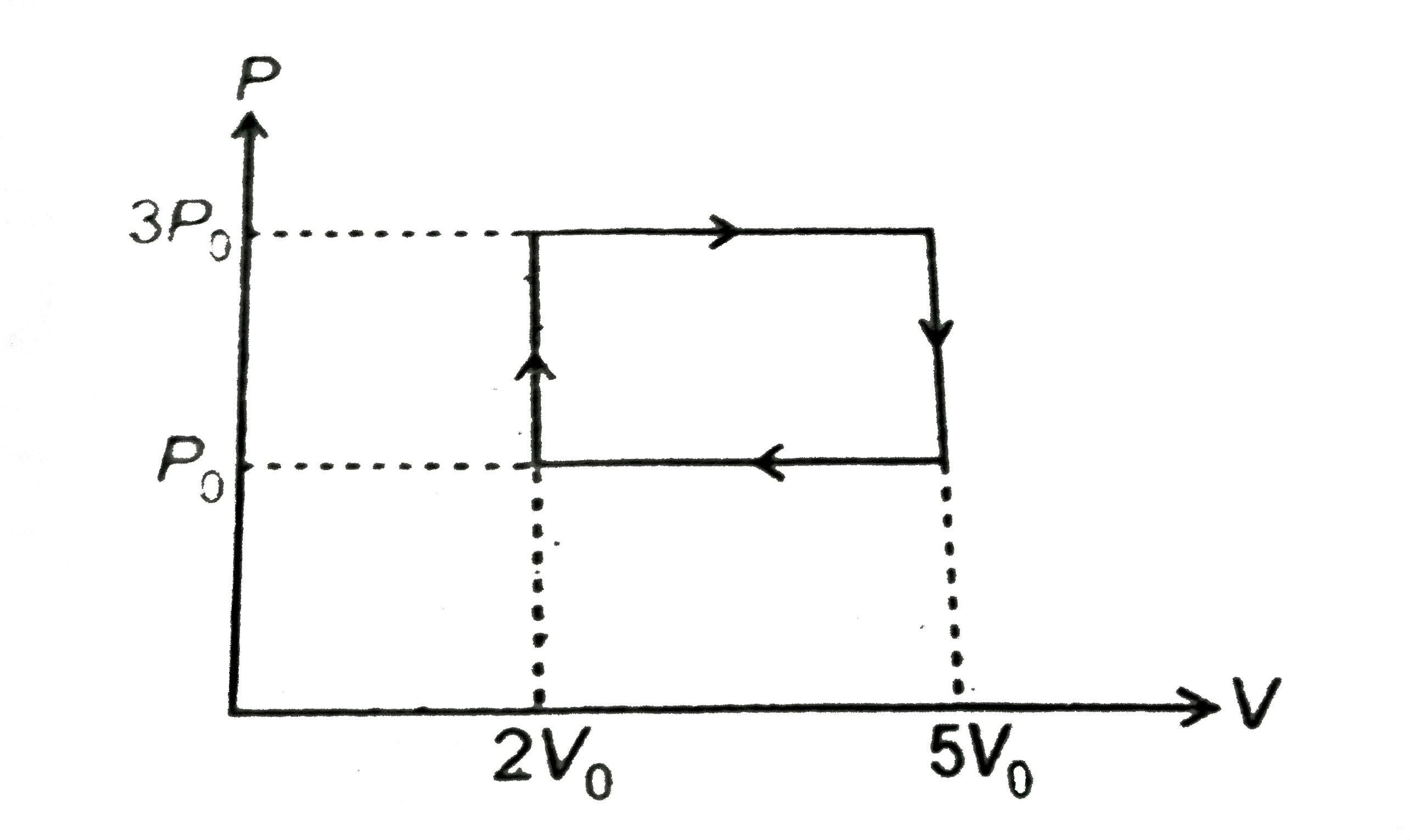
Work done in given cyclic process is
View SolutionWhat is the change in internal energy of a system undergoing a cyclic process, at the end of a cycle ?
View SolutionIn a cyclic process, work done by the system is
View SolutionHeat energy absorbed by a system in going through a cyclic process shown in figure is
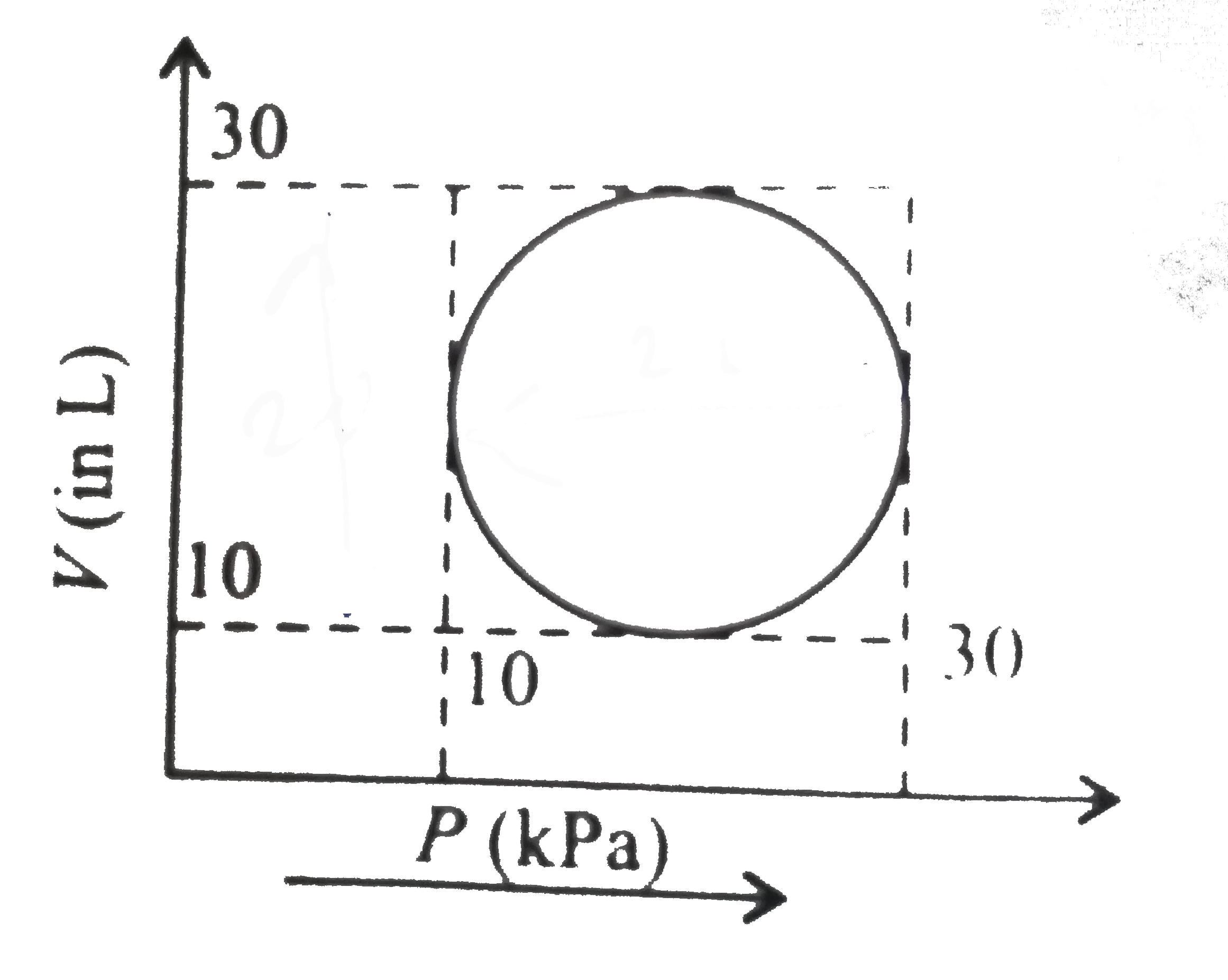
View SolutionHeat energy absorbed by a system in going through a cyclic process shown in figure is

View SolutionA system is expanded under adiabatic process
View SolutionWhat is the change in the internal energy of a system over one complete cycle of a cyclic process?
View Solution
