What is the length of the image of the rod in mirror, according to the observer in air? (refractive index of the liquid is μ)
_E01_058_Q01.png)
μL+L
L+Lμ
Lμ+Lμ
None of these
The correct Answer is:B
_E01_058_S01.png)
When observer in rarer medium and objects is in denser medium then the length of immersed portion will be shorter (apparent) Hence length of image of rod in water =2L+μL−L=L+μL
Hence length of image of rod seen by observer in air is = L+μLμ=Lμ+L . Hence [B]
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE-312videos
GEOMETRICAL OPTICS
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE-04[A]23videos
GEOMETRICAL OPTICS
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE- 0145videos
GEOMETRICAL OPTICS
- BOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II66videos
CURRENT ELECTRICITY
- BOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 49videos
GRAVITATION
Similar Questions
A stick is placed inside a hemispherical bowl as shown in Figure. The stick is horizontal and has a length of 2a. Eye of an observer is located at E such that it can just see the end A of the stick. A liquid is filled upto edge of the bowl and the end B of the stick becomes visible to the observer. Radius of the bowl is R. Find the refractive index (μ) of the liquid.
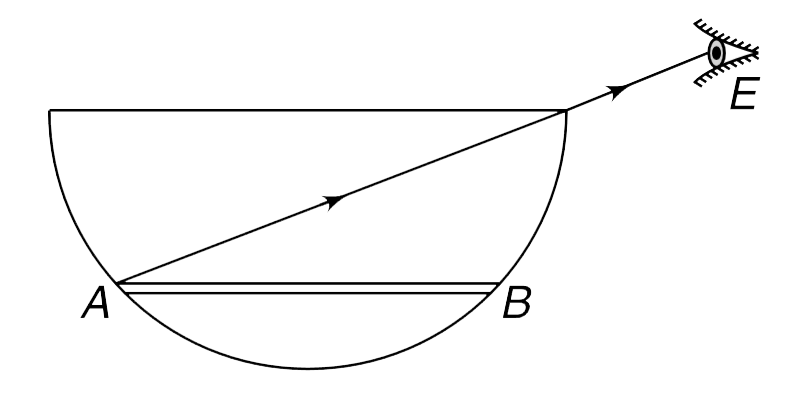View SolutionA concave mirror has the form of a hemisphere with a radius of R=60cm A thin layer of an unknown transparent liquid is poured into the mirror ,The mirror-liquids system forms one real Image and another real image is formed by mirror alone ,with the sources in a certain position .One of them coincides with the source and the other is at distance of l=30cm from source.find the possible value(s) refractive index μof the liquid.
View SolutionAn equiconcave diverging lens of focal length F is cut into two equal halves. The two halves are turned around and joined with some liquid between them.The lens obtained is converging with focal length F. If the refractive index of the liquid is 3 then what is the refractive index of the lens?
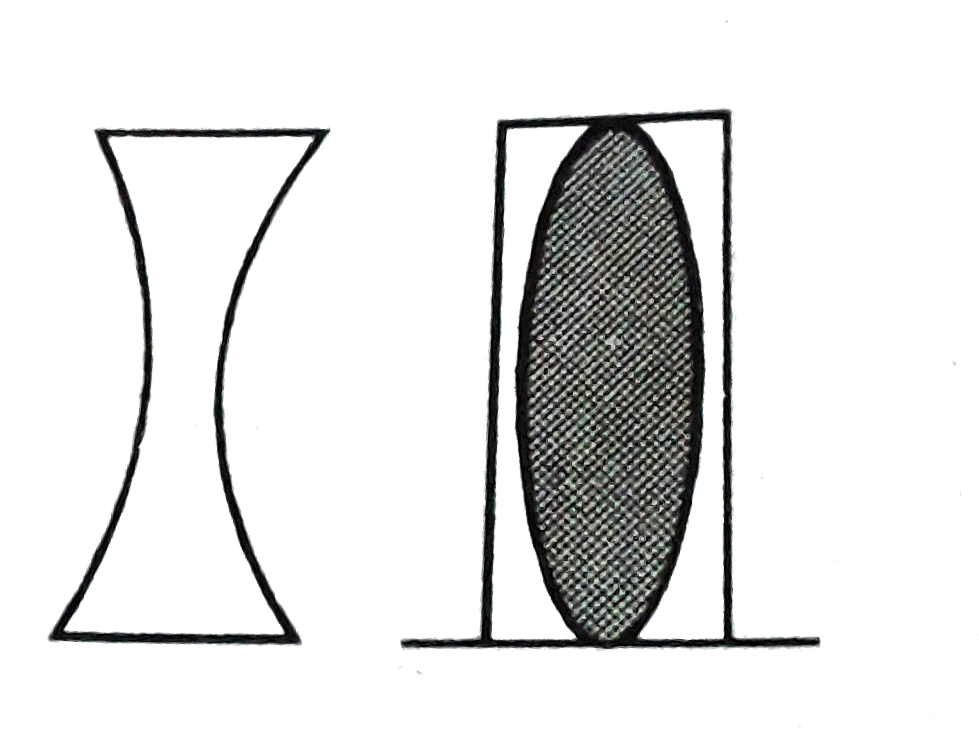View SolutionIf final image after two refractions through the lens and one reflection from the mirror forms at the same point O. Refrative index of the material of the lens μ=3/2. Then find d.
View SolutionThe radii of curvature of two spherical surfaces of a concave convex lens (μ=1.5) are 20 cm and 40 cm. (i) What is its focal length when it is in air? Also find its focal length when it is immersed in a liquid of refractive index (ii) μ=1.2 (iii) μ=2
View SolutionA thin equiconvex lens of refractive index 3/2 is placed on a horizontal plane mirror as shown in figure. The space between the lens and the mirror is filled with a liquid of refractive index 4/3 . It is found that when a point object is placed 15 cm above the lens on its priincipal axis, the object coincides with its own image.
Q. If another liquid is filled instead of water, the object and the image coincide at a distance 25 cm from the lens.
Calculate the refractive index of the liquid.View SolutionA circular beam of light (diameter d) falls on a plane surface of a liquid. The angle of incidence is 45∘ and refractive index of the liquid is μ. The diameter of the refracted beam is
View SolutionShown in the figure here is a convergent lens placed inside a cell filled with a liquid. The lens has focal length +20cm when in air and its material has refractive index 1.50. If the liquid has refractive index 1.60, the focal length of the system is
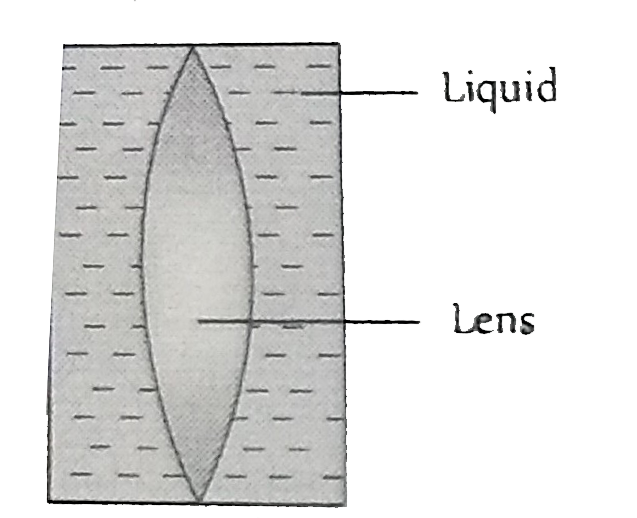View SolutionThe given figure shows a convergent lens placed inside a cell filled with liquid. The lens has focal length +20 cm when in air , and its metrial has refractive index 1.50 . If the liquid has refractive index 1.60 , then focal length of the lens in the cell is
View SolutionThe diagram alongside shows the refraction of a ray of light from air to a liquid.
(a) Write the values of (i) angle of incidence, and (ii) angle of refraction.
(b) Use snell's law to find the refractive index of liquid with respect to air.
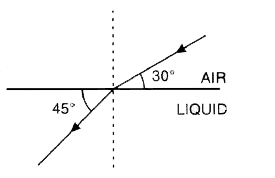View Solution