A particle starts from point x=−√32A and move towards negative extreme as shown,
_S01_011_Q01.png)
(a) Find the equation of the SHM
(b) Find the time taken by the particle to go directly from its initial position to negative extreme.
(c) Find the time taken by the particle to reach at mean position.
_S01_011_S01.png)
(a) Figure shows the solution of the problem with the help of phasor. Horizontal component of velocity at Q gives the required direction.
of velocity at t=0 so we will choose it.
In ΔOSQ:cosθ=√3/2AA=√32⇒θ=π6
Now ϕ=3π2−π6=8π6=4π3
So equation of SHM is x=Asin(ωt+4π3)
(b) Now to reach the particle at left extreme point it will travel angle θ along the circle. So time taken,
t=πω=π6ω⇒t=T12sec
(c) To reach the particle at mean position at mea n position it will travel angle α=π2+π6=2π3
So, time taken =αω=T3sec.
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - SOME WORKED OUT EXAMPLES29videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-01117videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)24videos
RACE
- BOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS4videos
TEST PAPER
Similar Questions
A particle start form mean position and moves towards positive extreme as shown. Find the equation of the SHM. Amplitude of SHM is A.
 View Solution
View SolutionA particle executes a simple harmonic motion of time period T. Find the time taken by the particle to go directly from its mean position to half the amplitude.
View SolutionA particle executes SHM with a time period of 4s. Find the time taken by the particle to go directly from its mean position to half of its amplitude.
View SolutionA particle executes S.H.M with time period 12 s. The time taken by the particle to go directly from its mean position to half its amplitude.
View SolutionA particle executes SHM with a time period of 4 s . Find the time taken by the particle to go from its mean position to half of its amplitude . Assume motion of particle to start from mean position.
View SolutionA particle of mass 2 kg executing SHM has amplitude 10 cm and time period is 1 s.Find (i) the angular frequency (ii) the maximum speed (ii) the maximum acceleration (iv) the maximum restoring force (v) the speed when the displacement from the mean position is 8 cm (vi) the speed after 112 s the particle was at the extreme position (vii) the time taken by the particle to go directly from its mean position to half the amplitude (viii) the time taken by the particle to go directly from its exterme position to half the amplitude.
View SolutionDisplacement-time equation of a particle execution SHM is x=A sin(ωt+π6)
Time taken by the particle to go directly from
x=−A2→x=+A2isView SolutionA particle is performing SHM of amplitude 'A' and time period 'T'. Find the time taken by the particle to go from 0→A/2.
View SolutionA particle is projected vertically upwards from ground with velocity 10 m/s. Find the time taken by it to reach at the highest point ?
View SolutionThe 1/v versus positions graph of a particle is shown in the figure, where v is the velocity of the particle. The particle is moving in a straight line aloing positive x- axis.Find the time taken by the particle to reach from the point A to B in second.
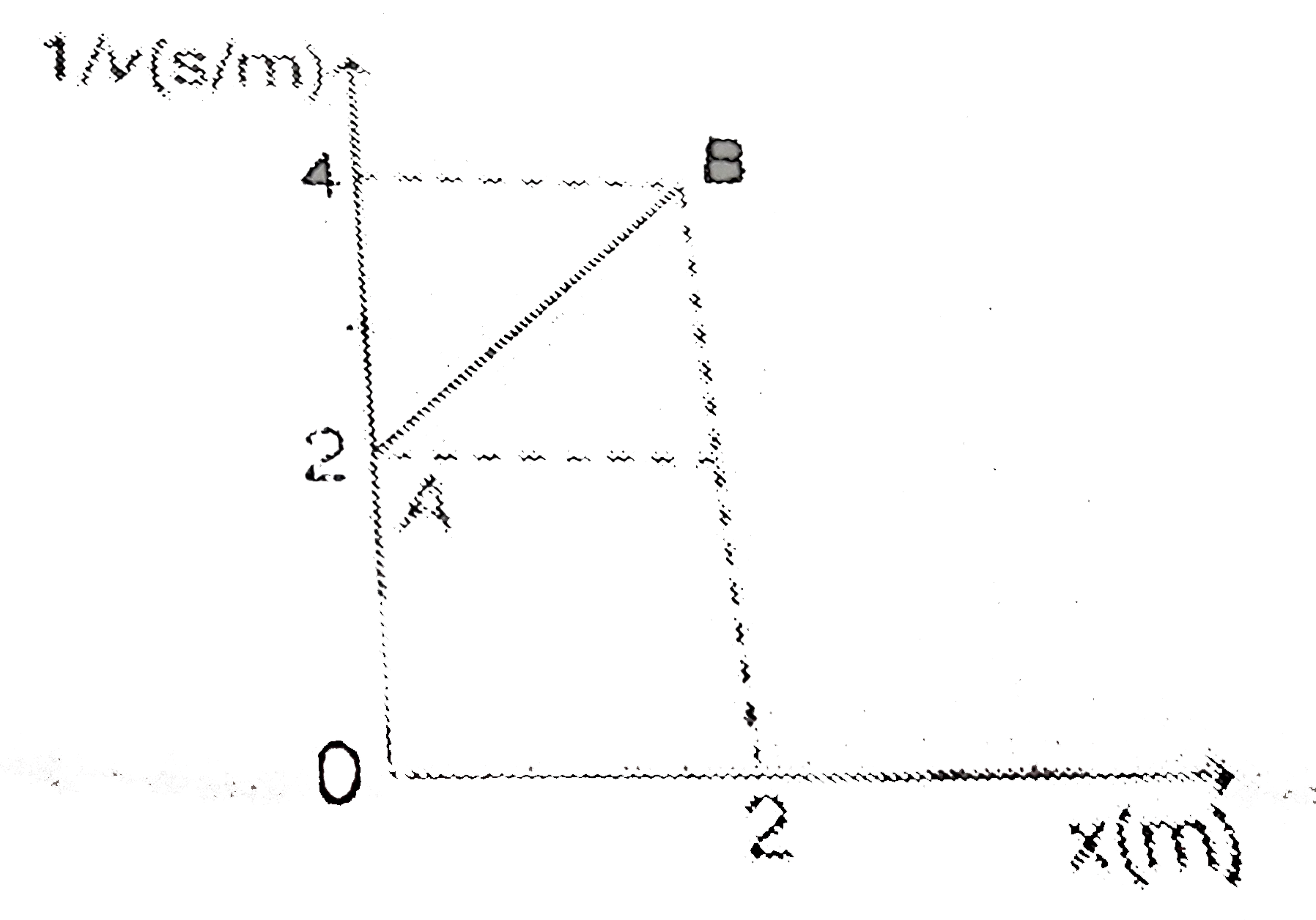 View Solution
View Solution

