A small bottle contains powered beryllium Be & gaseous radon which is used as a source of -particles. Netrons are produced when particles of the radon react with beryllium. The yield of this reaction is i.e. only one -particle out of induced the reaction. Find the amount of radon originally introduced into the source, if it prouduces neutrons per second after days. [ of days]
The correct Answer is:
To solve the problem, we will follow these steps:
Step 1: Understand the problem
We need to find the initial amount of radon (Rn-222) that produces 1.2 x 10^6 neutrons per second after 7.6 days, given that the yield of the reaction is 1/4000 and the half-life of radon is 3.8 days.
Step 2: Determine the number of half-lives
The time given is 7.6 days. Since the half-life of radon is 3.8 days, we can determine how many half-lives have passed:
Number of half-lives=7.6 days3.8 days=2
This means that after 7.6 days, the radon has undergone 2 half-lives.
Step 3: Calculate the remaining amount of radon
If we start with an initial amount N0, after 2 half-lives, the remaining amount of radon is:
N=N022=N04
Step 4: Calculate the decay constant
The decay constant λ can be calculated using the formula:
λ=ln(2)T1/2
Substituting the half-life:
λ=0.6933.8 days=0.6933.8×24×3600 seconds≈2.11×10−6 s−1
Step 5: Relate activity to the number of nuclei
The activity A is given by:
A=Nλ
Substituting N=N04:
A=N04λ
Given that the activity corresponds to the number of neutrons produced per second:
1.2×106=N04⋅2.11×10−6
Step 6: Solve for N0
Rearranging the equation to solve for N0:
N0=4⋅1.2×106⋅12.11×10−6
Calculating N0:
N0≈4⋅1.2×106⋅4.74×105≈9.095×1015 nuclei
Step 7: Convert to mass
To find the mass of radon, we use the molar mass of radon (approximately 222 g/mol):
Mass=N0⋅Molar massNA
Where NA is Avogadro's number (6.022×1023 nuclei/mol):
Mass=9.095×1015⋅222 g/mol6.022×1023 nuclei/mol≈3.354×10−4 g
Final Answer
The initial amount of radon introduced into the source is approximately 3.354×10−4 grams.
---
We need to find the initial amount of radon (Rn-222) that produces 1.2 x 10^6 neutrons per second after 7.6 days, given that the yield of the reaction is 1/4000 and the half-life of radon is 3.8 days.
The time given is 7.6 days. Since the half-life of radon is 3.8 days, we can determine how many half-lives have passed:
Number of half-lives=7.6 days3.8 days=2
This means that after 7.6 days, the radon has undergone 2 half-lives.
If we start with an initial amount N0, after 2 half-lives, the remaining amount of radon is:
N=N022=N04
The decay constant λ can be calculated using the formula:
λ=ln(2)T1/2
Substituting the half-life:
λ=0.6933.8 days=0.6933.8×24×3600 seconds≈2.11×10−6 s−1
The activity A is given by:
A=Nλ
Substituting N=N04:
A=N04λ
Given that the activity corresponds to the number of neutrons produced per second:
1.2×106=N04⋅2.11×10−6
Rearranging the equation to solve for N0:
N0=4⋅1.2×106⋅12.11×10−6
Calculating N0:
N0≈4⋅1.2×106⋅4.74×105≈9.095×1015 nuclei
To find the mass of radon, we use the molar mass of radon (approximately 222 g/mol):
Mass=N0⋅Molar massNA
Where NA is Avogadro's number (6.022×1023 nuclei/mol):
Mass=9.095×1015⋅222 g/mol6.022×1023 nuclei/mol≈3.354×10−4 g
The initial amount of radon introduced into the source is approximately 3.354×10−4 grams.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:Exercise-05 [A]
Explore 39 Videos
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:Exercise-05 [B]
Explore 12 Videos
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:Exercise-04 [A]
Explore 20 Videos
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
Explore 24 Videos
- TEST PAPERBook:ALLENChapter:TEST PAPERExercise:PHYSICS
Explore 4 Videos
Similar Questions
Source of α-particles used in scattering experiment was
View Solutionα-Particles can be detected using
View SolutionWhich of the following path of α-particle is/are possible in the α-particle scattering experiment?
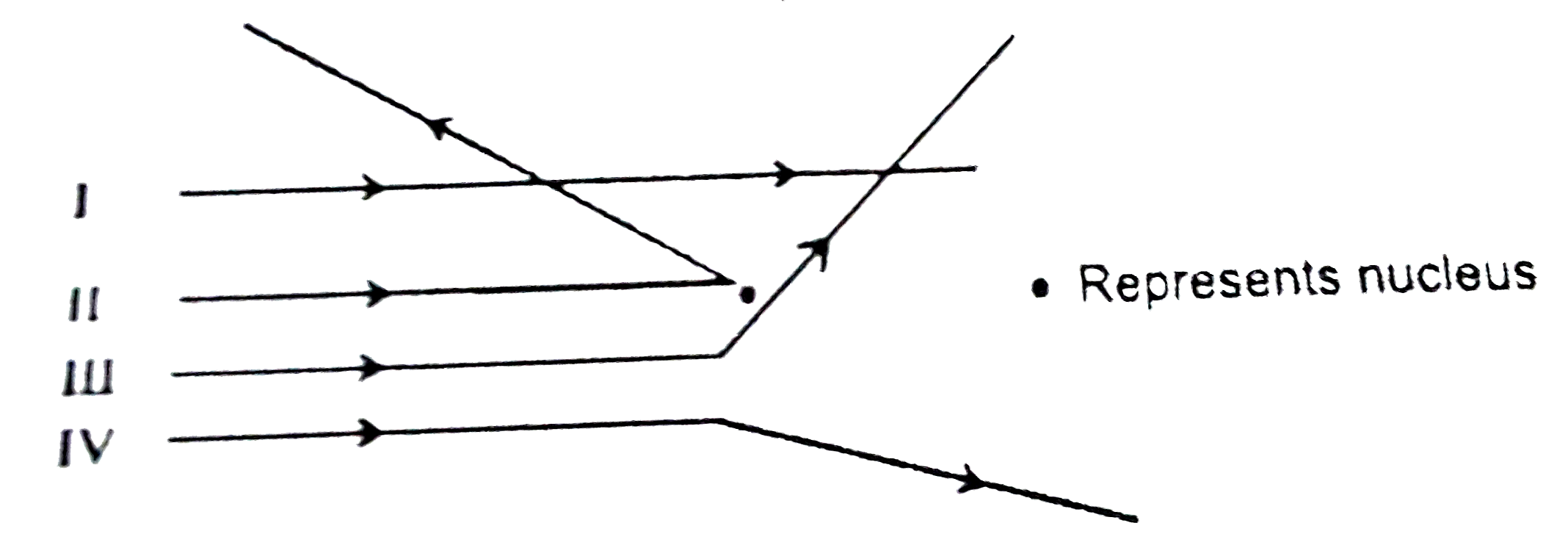
View SolutionThe ionising power of α−particle is less compared to α−particles but their penetrating power is more.
The mass of β−particle is less than the mass of α-particle.
View SolutionRadon was discovered by
View SolutionWhy are the alpha particles not used in radio therapy ?
[Hint : alpha particles cannot penetrate the human skin]
View SolutionAn α-particle is accelerated through a.p.d of 106 volt the K.E. of particle will be
View SolutionAlpha particles are ...... times heavier (approximately) than neutron
View SolutionThe ratio of the de Broglie wavelength of a proton and alpha particles will be 1:2 if their
View SolutionThe ratio of the de Broglie wavelength of a proton and alpha particles will be 1:2 if their
View Solution