has four statements (A,B,C and D) given in Coumn-I and five statements (P,Q,R,S and T) given in Column-II. Any given statement in Column-I can have correct matching with one or more statement(s) given in Column-II.
Column−IColumn−II(A)A rectangular box has volume 48,and the sum of(P)1length of the twelve edges of the box is 48. The largestinteger that could be the length of an edge of the box,is(B)The number of zeroes at the end in the product of first(Q)220 prime numbers, is(p)(C)The number of solutions of22x−32y=55in which x and y(R)3are integers,is(0)(S)4(D)The number(7+5√2)1/3+(7−5√2)1/3is equal to(T)6
The correct Answer is:T,P,P,Q
To solve the problem, we need to analyze the statements in Column-I and find their correct matches in Column-II. Let's break down each statement in Column-I and see which statements from Column-II correspond to them.
1. Statement A: "A rectangular box has volume 48, and the sum of the lengths of the twelve edges of the box is 48. The largest integer that could be the length of an edge of the box is..."
- We need to find the dimensions of the box (length, width, height) such that:
- Volume (l * w * h) = 48
- Sum of edges (4(l + w + h)) = 48, which simplifies to (l + w + h) = 12.
- To maximize one edge, let's assume l is the largest edge. We can express w and h in terms of l:
- w + h = 12 - l
- Then, we can substitute into the volume equation: l * (12 - l) * h = 48.
- Solving this will give us the maximum possible integer value for l.
2. Statement B: "The number of zeroes at the end in the product of the first 20 prime numbers, is..."
- The number of trailing zeros in a factorial or product can be determined by the number of pairs of factors of 5 and 2.
- Since the first 20 prime numbers include only one factor of 5 (which is 5 itself) and no factors of 2, the number of trailing zeros is 0.
3. Statement C: "The number of solutions of 2^(2x) - 3^(2y) = 55 in which x and y are integers, is..."
- We need to find integer solutions for the equation. We can rewrite it as:
- 2^(2x) = 3^(2y) + 55.
- Testing integer values for x and y will help us find the number of solutions.
4. Statement D: "The number (7 + 5sqrt(2))^(1/3) + (7 - 5sqrt(2))^(1/3) is equal to..."
- This expression can be simplified using the identity for the sum of cube roots. We can let:
- a = (7 + 5sqrt(2))^(1/3) and b = (7 - 5sqrt(2))^(1/3).
- Then, we can find a + b by using the properties of cube roots.
Matching Statements:
- A matches with (P): The largest integer that could be the length of an edge of the box.
- B matches with (Q): The number of zeroes at the end in the product of the first 20 prime numbers is 0.
- C matches with (R): The number of solutions of the equation.
- D matches with (T): The value of the expression involving cube roots.
Final Matches:
- A → P
- B → Q
- C → R
- D → T
- We need to find the dimensions of the box (length, width, height) such that:
- Volume (l * w * h) = 48
- Sum of edges (4(l + w + h)) = 48, which simplifies to (l + w + h) = 12.
- To maximize one edge, let's assume l is the largest edge. We can express w and h in terms of l:
- w + h = 12 - l
- Then, we can substitute into the volume equation: l * (12 - l) * h = 48.
- Solving this will give us the maximum possible integer value for l.
- The number of trailing zeros in a factorial or product can be determined by the number of pairs of factors of 5 and 2.
- Since the first 20 prime numbers include only one factor of 5 (which is 5 itself) and no factors of 2, the number of trailing zeros is 0.
- We need to find integer solutions for the equation. We can rewrite it as:
- 2^(2x) = 3^(2y) + 55.
- Testing integer values for x and y will help us find the number of solutions.
- This expression can be simplified using the identity for the sum of cube roots. We can let:
- a = (7 + 5sqrt(2))^(1/3) and b = (7 - 5sqrt(2))^(1/3).
- Then, we can find a + b by using the properties of cube roots.
- B matches with (Q): The number of zeroes at the end in the product of the first 20 prime numbers is 0.
- C matches with (R): The number of solutions of the equation.
- D matches with (T): The value of the expression involving cube roots.
- A → P
- B → Q
- C → R
- D → T
Topper's Solved these Questions
Similar Questions
Any given statement in column I can have correct matching with one or more statement(s) given in column II. Match the following.

View SolutionAny given statement in column I can have correct matching with one or more statement(s) given in column II. Q. Match the following.

View SolutionMatch the statements given in Column I abd Column II.

View SolutionMatch the reactions given in Column I with the statements given in Column II
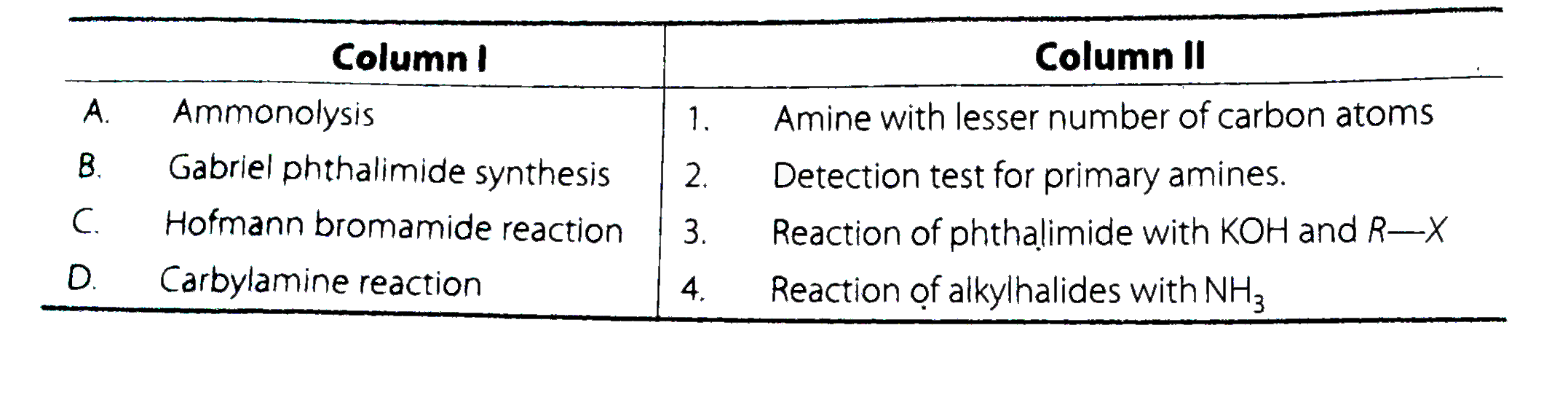
View SolutionMatch the reactions given in Column I with the statements given in Column II

View SolutionMatch the entries in column II with the statements given in column I.

View SolutionMatch the compounds/elements given in Column I with uses given in Column II.

View SolutionMatch the compounds given in Column-I with the items given in Column - II.

View Solutionmatch the types of defect given in column I with the statement given in column II.
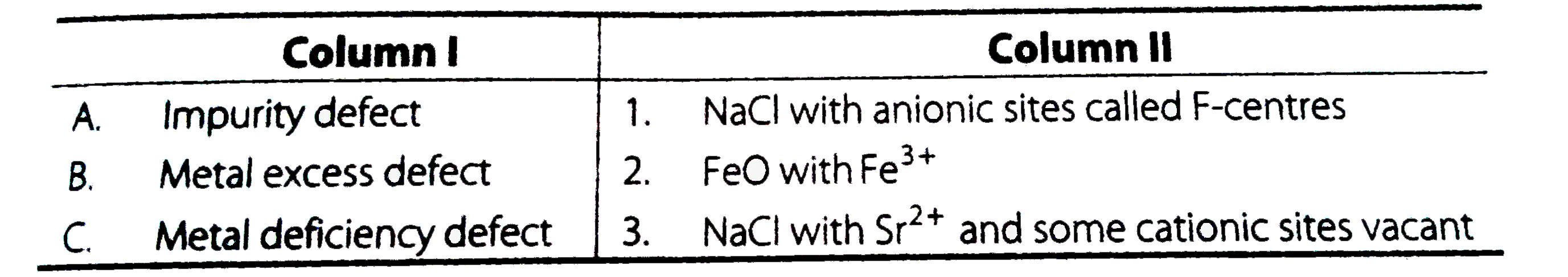
View Solutionmatch the types of defect given in column I with the statement given in column II.
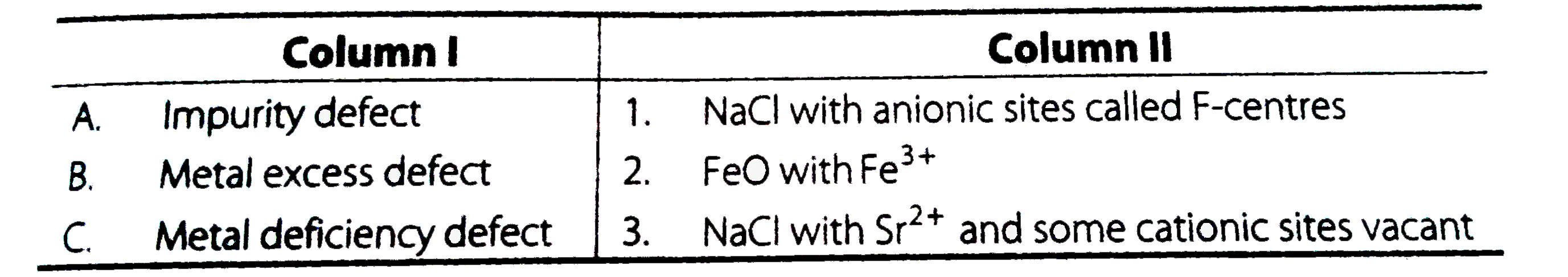
View Solution
