Question

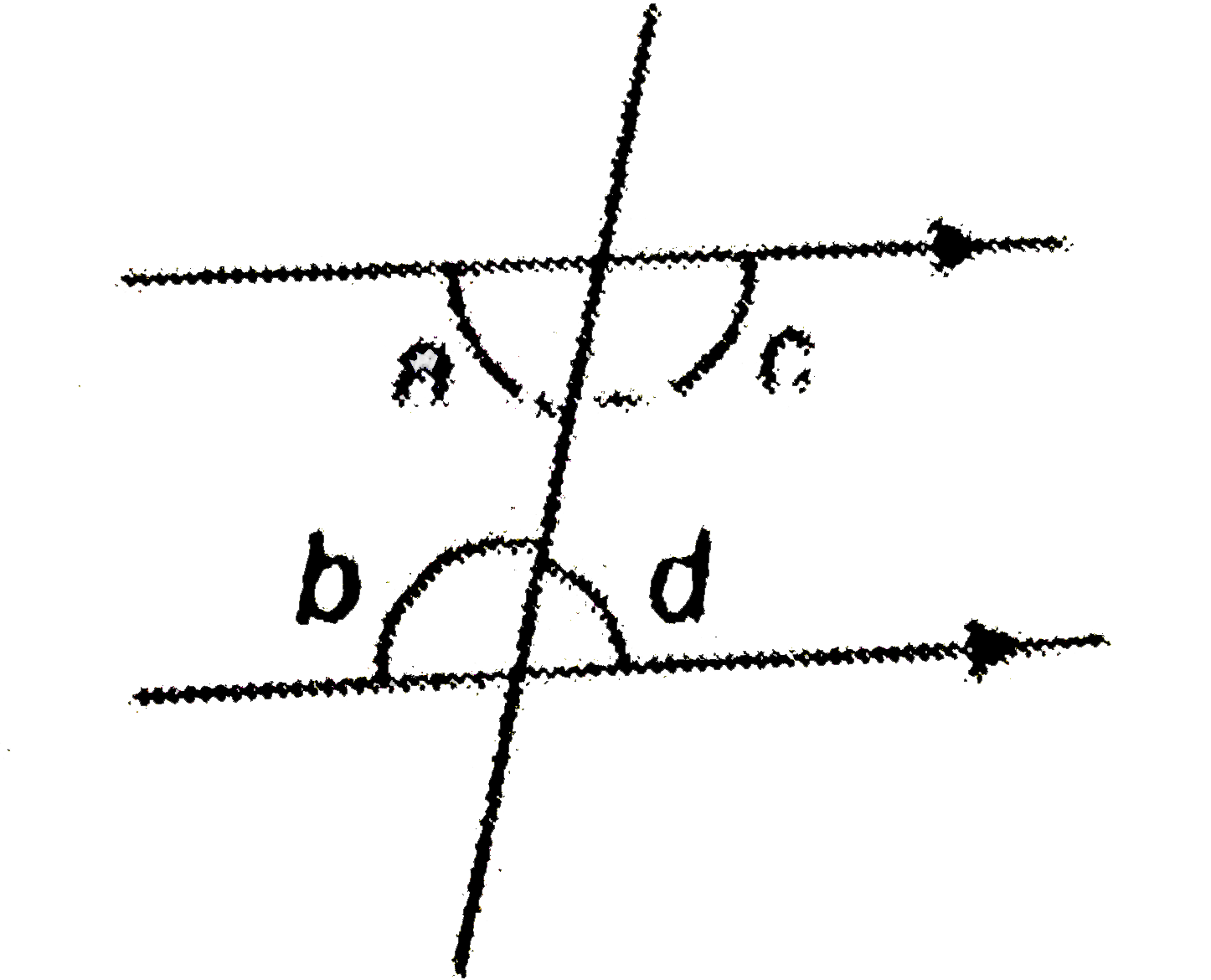
If a,b are complementary angles and b,c are supplementary angles. If the average of a and c is ${85}^{\circ }$, then find $a+b+c$.

Options

A. `100^(@)`
B. `160^(@)`
C. `156^(@)`
D. `220^(@)`

Explanation

To solve the problem step by step, we will use the properties of complementary and supplementary angles along with the given average.

Step 1: Understand the relationships between the angles
- Since \( a \) and \( b \) are complementary angles, we have:
\( a + b = 90^\circ \quad \text{(1)} \)
- Since \( b \) and \( c \) are supplementary angles, we have:
\( b + c = 180^\circ \quad \text{(2)} \)

Step 2: Use the average of \( a \) and \( c \)
- The average of \( a \) and \( c \) is given as \( 85^\circ \). Therefore:
\( \frac{a + c}{2} = 85^\circ \)
Multiplying both sides by 2 gives:
\( a + c = 170^\circ \quad \text{(3)} \)

Step 3: Add equations (1), (2), and (3)
- Now, we will add equations (1), (2), and (3):
\( (a + b) + (b + c) + (a + c) = 90^\circ + 180^\circ + 170^\circ \)
- Simplifying the left side:
\( 2a + 2b + c = 440^\circ \)
- This can be simplified to:
\( 2(a + b + c) = 440^\circ \)

Step 4: Solve for \( a + b + c \)
- Dividing both sides by 2 gives:
\( a + b + c = 220^\circ \)

Final Answer
Thus, the value of \( a + b + c \) is:
\( \boxed{220^\circ} \)

---