The expression simplifies to
an irrational number
a prime number
a natural number which is not composite
a real number of the form where a and b are prime
To simplify the expression
√sin4(37.5∘)+4cos2(37.5∘)+√cos4(37.5∘)+4sin2(37.5∘),
we will follow these steps:
Step 1: Rewrite the cosine terms
We can use the identity cos2(θ)=1−sin2(θ) to rewrite the cosine terms.
For the first square root:
√sin4(37.5∘)+4cos2(37.5∘)=√sin4(37.5∘)+4(1−sin2(37.5∘)).
Step 2: Simplify the first square root
Now we simplify the expression inside the first square root:
sin4(37.5∘)+4(1−sin2(37.5∘))=sin4(37.5∘)+4−4sin2(37.5∘).
Let x=sin2(37.5∘). Then the expression becomes:
x2−4x+4=(x−2)2.
Thus, we have:
√sin4(37.5∘)+4cos2(37.5∘)=|x−2|=|sin2(37.5∘)−2|.
Step 3: Rewrite the sine terms
Now we apply the same process to the second square root:
√cos4(37.5∘)+4sin2(37.5∘)=√cos4(37.5∘)+4(1−cos2(37.5∘)).
Step 4: Simplify the second square root
Using y=cos2(37.5∘), we have:
y2+4(1−y)=y2+4−4y=(y−2)2.
Thus, we have:
√cos4(37.5∘)+4sin2(37.5∘)=|y−2|=|cos2(37.5∘)−2|.
Step 5: Combine the results
Now we combine the results from both square roots:
|sin2(37.5∘)−2|+|cos2(37.5∘)−2|.
Since sin2(37.5∘)≤1 and cos2(37.5∘)≤1, both |sin2(37.5∘)−2| and |cos2(37.5∘)−2| will simplify to 2−sin2(37.5∘) and 2−cos2(37.5∘) respectively:
(2−sin2(37.5∘))+(2−cos2(37.5∘))=4−(sin2(37.5∘)+cos2(37.5∘)).
Step 6: Use the Pythagorean identity
Using the identity sin2(θ)+cos2(θ)=1:
4−1=3.
Final Answer
Thus, the expression simplifies to:
3.
We can use the identity cos2(θ)=1−sin2(θ) to rewrite the cosine terms.
Now we simplify the expression inside the first square root:
Now we apply the same process to the second square root:
Using y=cos2(37.5∘), we have:
Now we combine the results from both square roots:
Using the identity sin2(θ)+cos2(θ)=1:
Thus, the expression simplifies to:
Topper's Solved these Questions
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - RACE 19
14 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Race 21
14 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - RACE 13
10 Videos
- LOGARITHMSBOOK - ALLENCHAPTER - LOGARITHMSEXERCISE - All Questions
92 Videos
- SEQUENCE AND PROGRESSIONBOOK - ALLENCHAPTER - SEQUENCE AND PROGRESSIONEXERCISE - Exercise (JA)
12 Videos
Similar Questions
Knowledge Check
Evalaute: [4sin30∘,2cos60∘sin90∘,2cos0∘][4554]
A[4554]B[2112]C[13141413]D[14131314]If sin37∘=z, express sin74∘ in terms of z.
A2z√1−z2B2z2+1C2zD2z2−1
The value of sin1∘+sin3∘+sin5∘+sin7∘cos1∘⋅cos2∘sin4∘ is __________
View SolutionFind the resultant of the following forces.
[sin37∘=35,cos37∘=45,sin53∘=45,cos53∘=35]
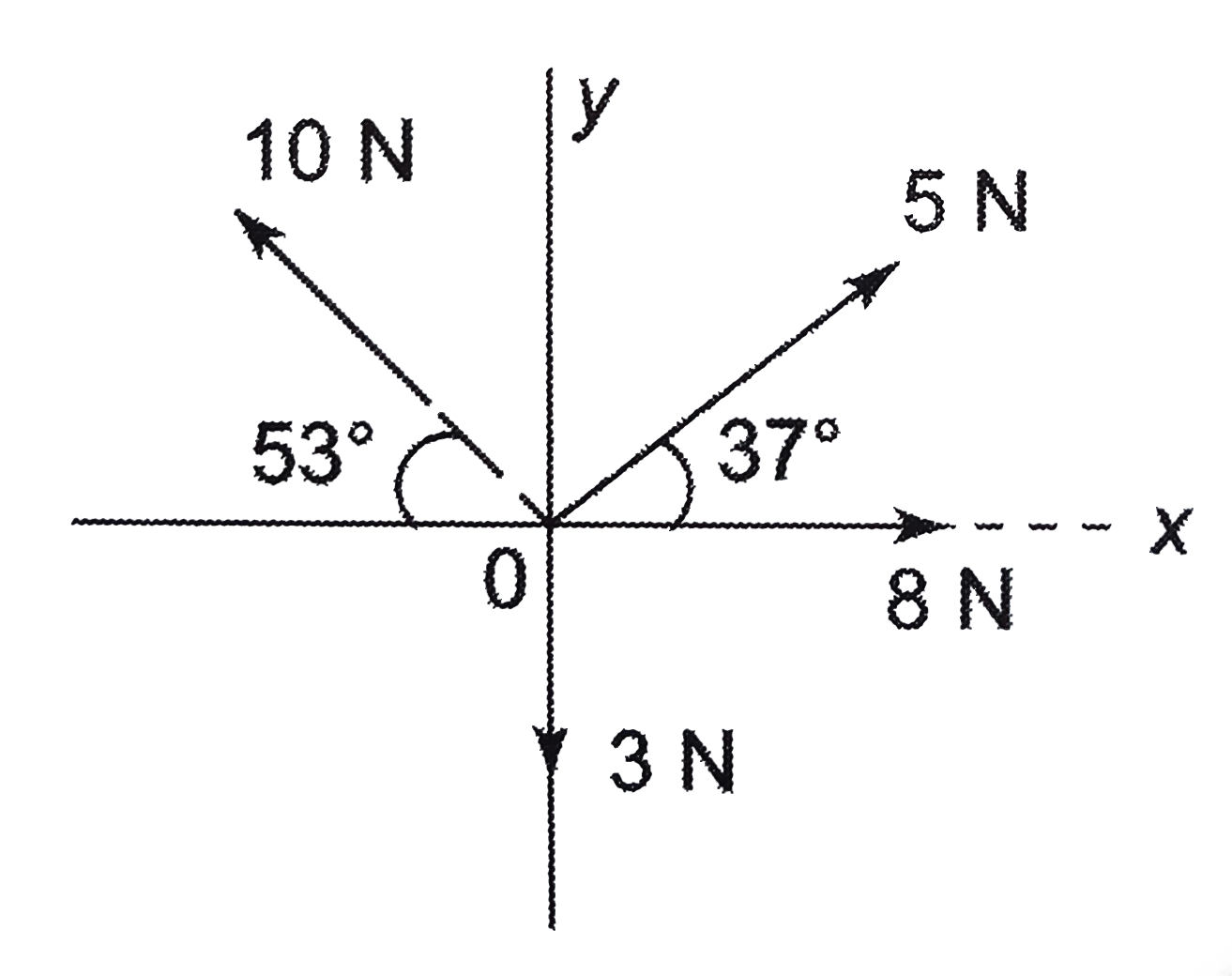
View SolutionProve that √sin4x+4cos2x−√cos4x+4sin2x=cos2x.
View SolutionSolve : 4−√54+√5+25+√3+4+√54−√5
View SolutionEvaluate the following expression:
cos(sin−145+cos−123)
View SolutionProve that : 4(sin−1(1√10)+cos−1(2√5))=π
View Solution
