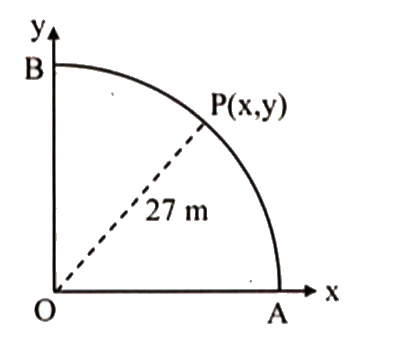
A point P moves in a counter-clockwise direction on a circular path as shown in the figure. The movement of P is such that it sweeps out a length s=t3+5 where s is in the metre and t is in seconds. The radius of the path is 27 m. The acceleration of P when t= 3 s is _________ m/s2. (Take √13=3.6)
2m/s2
1.5m/s2
2.5m/s2
3m/s2
The correct Answer is:C
Step by step video & image solution for A point P moves in a counter-clockwise direction on a circular path as shown in the figure. The movement of P is such that it sweeps out a length s= t^(3) +5 where s is in the metre and t is in seconds. The radius of the path is 27 m. The acceleration of P when t= 3 s is _________ m//s^(2). (Take sqrt(13) = 3.6) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - ALLENCHAPTER - CIRCULAR MOTIONEXERCISE - MCQ
14 Videos
- CIRCULAR MOTIONBOOK - ALLENCHAPTER - CIRCULAR MOTIONEXERCISE - Martrix match
1 Videos
- CIRCULAR MOTIONBOOK - ALLENCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE(S-2)
6 Videos
- BASIC MATHSBOOK - ALLENCHAPTER - BASIC MATHSEXERCISE - Question
1 Videos
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II
66 Videos
Similar Questions
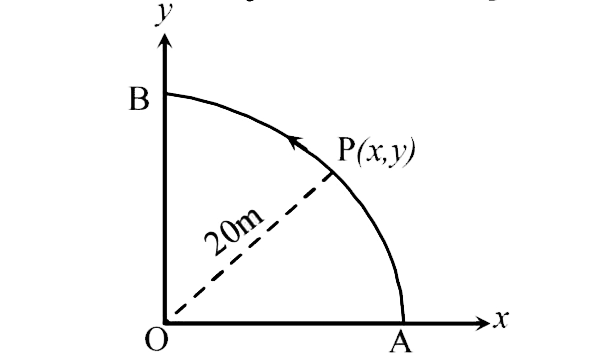
A point P moves in counter-clockwise direction on a circular path as shown in the figure. The movement of 'P ' is such that it sweeps out a length s=t3+5 where s is in meters and t is in seconds. The radius of the path is 20 m. The acceleration of ' P ' when t = 2 s is nearly:
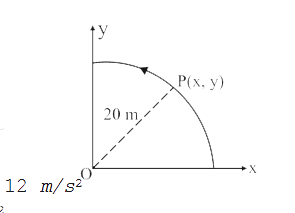
View SolutionA point p moves in counter - clockwise direction on a circular path as shown in the figure . The movement of 'p' is such that it sweeps out in the figure . The movement of 'p' is such that it sweeps out a length s=t3+5 , where s is in metres and t is in seconds . The radius of the path is 20m . The acceleration of 'P' when t=2s is nearly .
View SolutionA car moves along a straight line whose equation of motion is given by
s=12t+3t2−2t3
where s is in metres and t is in seconds. The velocity of the car at start will be :-
View SolutionThe displacement of a particle moving in a straight line is described by the relation s=6+12t−2t2. Here s is in metre and t in second. The distance covered by the particle in first 5s is
View SolutionThe displacement of a particle moving in a straight line is described by the relation s=6+12t−2t2. Here s is in metre and t in second. The distance covered by the particle in first 5s is
View SolutionA particle is moving such that s=t3−6t2+18t+9, where s is in meters and t is in meters and t is in seconds. Find the minimum velocity attained by the particle.
View SolutionA particle moves in a circle of radius 20 cm. Its linear speed is given by v=(3t2+5t) where t is in second and v is in m/s. Find the resultant acceleration at t = 1s.
View SolutionA particle of mass 1 kg moves in a circular path of radius 1 m such that its speed varies with time as per equation v=3t2m/s where time t is in seconds. The power delivered by the force acting on the paritcle at t=1s, is :−
View SolutionA particle moves in a circle of radius 20 cm. Its linear speed is given by v=2t, where t is in second and v in metre/ second. Find the radial and tangential acceleration at t=3s.
View SolutionIF the equation for the displancement of a particle moving on a circular path is given by θ=2t3+0.5, where θ is in radius and t is in seconds, then the angular velocity of the particle at t=2 s is
View Solution
