Question

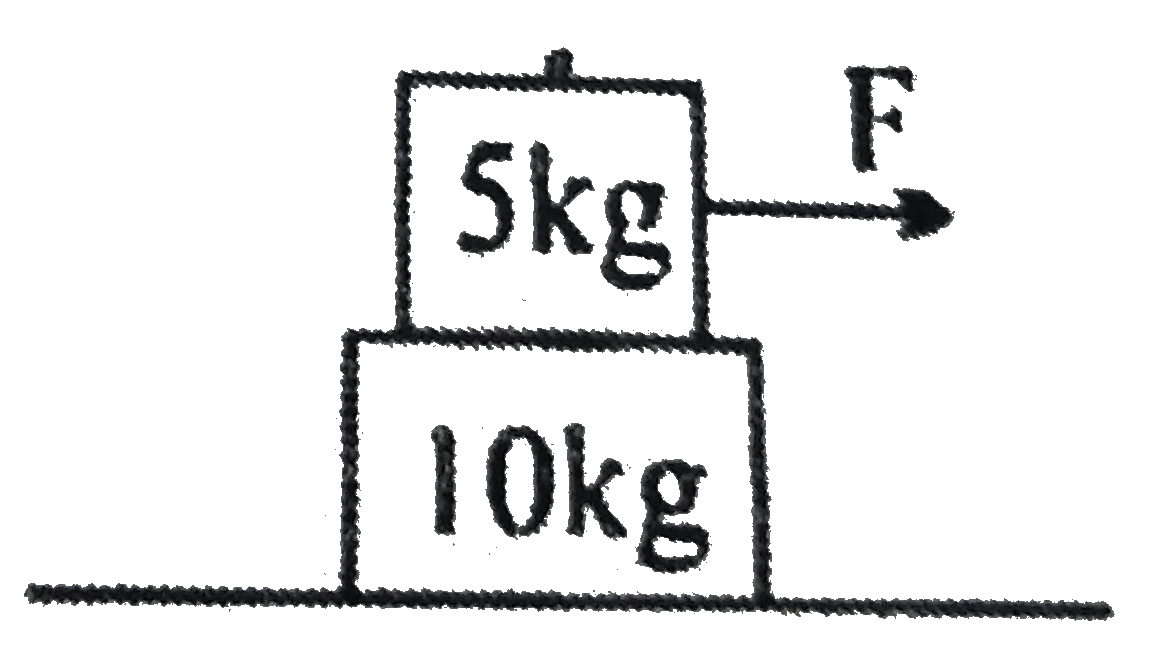
Coefficient of friction between $5$ $kg$ and $10$ $kg$ block is $0.5$. If friction between them is $20$ $N$. What is the value of force being applied on $5$ $kg$? The floor is frictionless

Answer

30 N

Explanation

To solve the problem, we need to determine the force being applied on the 5 kg block when it is placed on top of the 10 kg block, given that the coefficient of friction between the two blocks is 0.5 and the friction force between them is 20 N.

1. Identify the Forces Acting on the 5 kg Block:
- The weight of the 5 kg block (W1) is given by:
\( W_1 = m_1 \cdot g = 5 \, \text{kg} \cdot 9.8 \, \text{m/s}^2 = 49 \, \text{N} \)
- The normal force (N) acting on the 5 kg block from the 10 kg block is equal to its weight:
\( N = W_1 = 49 \, \text{N} \)

2. Calculate the Maximum Static Friction:
- The maximum static friction (f_max) between the two blocks can be calculated using the coefficient of friction (μ):
\( f_{\text{max}} = \mu \cdot N = 0.5 \cdot 49 \, \text{N} = 24.5 \, \text{N} \)
- Since the friction force given is 20 N, which is less than 24.5 N, the blocks do not slip relative to each other.

3. Determine the Common Acceleration:
- The total mass of the system (both blocks) is:
\( m_{\text{total}} = m_1 + m_2 = 5 \, \text{kg} + 10 \, \text{kg} = 15 \, \text{kg} \)
- The net force acting on the system is the friction force (20 N) acting on the 10 kg block. Thus, we can find the common acceleration (a):
\( a = \frac{f_{\text{friction}}}{m_{\text{total}}} = \frac{20 \, \text{N}}{15 \, \text{kg}} = \frac{4}{3} \, \text{m/s}^2 \approx 1.33 \, \text{m/s}^2 \)

4. Calculate the Force Applied on the 5 kg Block:
- The force (F) applied on the 5 kg block must overcome the friction force acting on the 10 kg block and also provide the necessary acceleration to both blocks:
\( F = m_1 \cdot a + f_{\text{friction}} = 5 \, \text{kg} \cdot \frac{4}{3} \, \text{m/s}^2 + 20 \, \text{N} \)
- Calculate:
\( F = \frac{20}{3} \, \text{N} + 20 \, \text{N} = \frac{20 + 60}{3} = \frac{80}{3} \, \text{N} \approx 26.67 \, \text{N} \)

Final Answer:
The force being applied on the 5 kg block is approximately 26.67 N.