From the concept of directed dimension what is the formula for a range (R) of a cannon ball when it is fired with vertical velocity component Vy and a horizontal velocity component Vx, assuming it is fired on a flat surface. [Range also depends upon acceleration due to gravity , g and k is numerical constant]
R=k(VxVy)g
R=k(Vx)2g
R=k(Vx)3Vyg
R=k(Vy)3Vxg
The correct Answer is:A
To derive the formula for the range R of a cannonball fired with vertical velocity component Vy and horizontal velocity component Vx, we will follow these steps:
Step 1: Understand the Components of Velocity
The cannonball is fired with two components of velocity:
- Horizontal component: Vx
- Vertical component: Vy
Step 2: Determine the Time of Flight
The time of flight t can be determined using the vertical motion of the cannonball. The vertical motion is influenced by gravity g. The vertical velocity changes from Vy to −Vy when it reaches the maximum height and then falls back down.
Using the first equation of motion:
Vfinal=Vinitial+a⋅t
Here, Vfinal=−Vy, Vinitial=Vy, and a=−g (acceleration due to gravity).
Thus, we have:
−Vy=Vy−g⋅t
Rearranging gives:
g⋅t=2Vy⟹t=2Vyg
Step 3: Calculate the Range
The range R is the horizontal distance traveled by the cannonball during the time of flight. The horizontal distance is given by:
R=Vx⋅t
Substituting the expression for t:
R=Vx⋅2Vyg
Step 4: Introduce the Numerical Constant k
In the problem, we are told that the range also depends on a numerical constant k. Therefore, we can express the range as:
R=k⋅2VxVyg
Step 5: Final Expression
Thus, we can write the final formula for the range R as:
R=k⋅VxVyg
Conclusion
The derived formula for the range R of a cannonball fired with vertical and horizontal components of velocity is:
R=k⋅VxVyg
The cannonball is fired with two components of velocity:
- Horizontal component: Vx
- Vertical component: Vy
The time of flight t can be determined using the vertical motion of the cannonball. The vertical motion is influenced by gravity g. The vertical velocity changes from Vy to −Vy when it reaches the maximum height and then falls back down.
Vfinal=Vinitial+a⋅t
Here, Vfinal=−Vy, Vinitial=Vy, and a=−g (acceleration due to gravity).
−Vy=Vy−g⋅t
Rearranging gives:
g⋅t=2Vy⟹t=2Vyg
The range R is the horizontal distance traveled by the cannonball during the time of flight. The horizontal distance is given by:
R=Vx⋅t
Substituting the expression for t:
R=Vx⋅2Vyg
In the problem, we are told that the range also depends on a numerical constant k. Therefore, we can express the range as:
R=k⋅2VxVyg
Thus, we can write the final formula for the range R as:
R=k⋅VxVyg
The derived formula for the range R of a cannonball fired with vertical and horizontal components of velocity is:
R=k⋅VxVyg
Topper's Solved these Questions
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (O-2)Matrix Type Questions.
3 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-M)
1 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (O-2) Multiple Correct Type Questions.
7 Videos
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - MATHS
14 Videos
- WAVE OPTICSBOOK - ALLENCHAPTER - WAVE OPTICSEXERCISE - Exercise 2 (Previous Year Questions)
7 Videos
Similar Questions
A particle is projected with a velocity v so that its range on a horizontal plane is twice the greatest height attained. If g is acceleration due to gravity, then its range is
View SolutionIn the figure, CDEF is a fixed conducting smooth frame in vertical plane.A conducting uniform rod GH of mass m=1g can move vertically and smoothly without losing contact with the frame.GH always remains horizontal.It is given velocity u=1m/s upwards and released.Taking the acceleration due to gravity as g and assuming that no resistance is present other than R.Time taken by rod to reach the highest point is equal to ln10x second.Find out value of x.
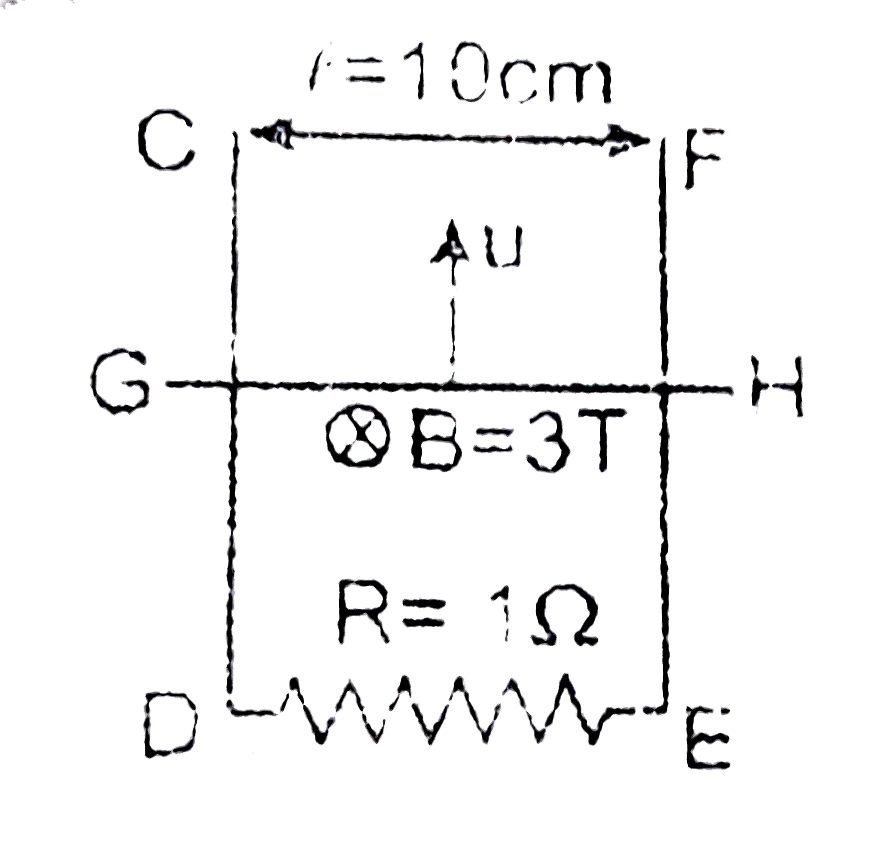
View Solution
Knowledge Check
An object lauched upwards at an angle has parabolic motion. The height h, of a projectile at time t is given by the equation h=12at2+vyt+h0, where a is the acceleration due to gravity, vv is the vertical component of the velocity, and h0 is the initial height. Which of the following equations correctly represents the object's acceleration due to gravity in terms of the other variables ?
Aa=h−vvt−h0tBa=h−vvt−h02t2Ca=2(h−vvt−h0)t2Da=t√2(h−vvt−h0)Students in a physics class are studying how the angle at which a projectile is launched on level ground affects the projectile's hang time and horizontal range. Hang time can be calculated using the formula t=2v.sin(θ)g, where t is the hang time in seconds, v is the initial launch velocity, θ is the projectile angle with respect to level ground, and g is the acceleration due to gravity, defined as 9.8m/s2. Horizontal range can be calculated using the formula R=v2sin(2θ)g, where R is the distance the projectile travels from the launch site, in feet. Which of the following gives the value on v, in terms of R, t and θ?
Av=tsin(θ)2Rsin(θ)Bv=2tsin(θ)Rsin(θ)Cv=2Rsin(θ)tsin(2θ)Dv=2Rsin(2θ)tsin(θ)
A shell is fired vertically upwards with a velocity v1 from a trolley moving horizontally with velocity v2. A person on the the ground observes the motion of the shell as a parabole, whose horizontal range is
View SolutionAssuming that the mass m of the largest stone that can be moved by a flowing river depends upon the velocity v of the water , its density ρ , and the acceleration due to gravity g . Then m is directly proportinal to
View SolutionA balloon starts rising from the earth's surface. The ascension rate is constant and equal to v0. Due to the wind. The balloon gathers the horizontal velocity component vx=ky, where k is a constnat and y is the height of ascent. Find how the following quantities depednd on the height of ascent.
(a) the horizontal drift of the balloon x (y)
(b) the total tangential and normal accelrations of the balloon.
View SolutionA projectile is projected tangentially from the surface of a planet of radius R. If it is at a height of 3R at the farthest point of its trajectory, then the velocity of projection V0 is given by ( acceleration due to gravity on surface=g)
View SolutionA projectile of a mass m is fired with velocity v from point a as shown in figure neglecting air resistance, what is the change in momentum in x direction when leaving from P and arriving at Q?

View SolutionA stone is projected from level ground with speed u and ann at angle θ with horizontal. Somehow the acceleration due to gravity (g) becomes double (that is 2g) immediately after the stone reaches the maximum height and remains same thereafter. Assume direction of acceleration due to gravity always vertically downwards.
Q. The horizontal range of particle is
View Solution
