The compound MX4 is tetrahedral. The number of ∠XMX angles formed in the compound is
Three
Four
Five
Six
The correct Answer is:A
To determine the number of XMX angles formed in the tetrahedral compound MX₄, we can follow these steps:
Step 1: Understand the Geometry of the Compound
The compound MX₄ has a tetrahedral geometry. In a tetrahedral shape, the central atom (M) is surrounded by four identical atoms (X) at the corners of a tetrahedron.
Hint: Remember that tetrahedral geometry is characterized by bond angles of approximately 109.5°.
Step 2: Identify the Central Atom and Surrounding Atoms
In the compound MX₄:
- M is the central atom.
- There are four X atoms surrounding M.
Hint: Visualizing the tetrahedral shape can help in understanding the arrangement of the atoms.
Step 3: Determine the Number of XMX Angles
Each pair of X atoms forms an angle with the central atom M. Since there are four X atoms, we can calculate the number of unique XMX angles formed.
To find the number of XMX angles, we can use the combination formula:
- The number of ways to choose 2 X atoms from 4 is given by the combination formula C(n, r), where n is the total number of atoms and r is the number of atoms to choose.
Using the formula:
C(4,2)=4!2!(4−2)!=4×32×1=6
Thus, there are 6 unique XMX angles formed in the compound.
Hint: Remember that each angle is formed by selecting any two of the four surrounding atoms.
Conclusion
The total number of XMX angles formed in the tetrahedral compound MX₄ is 6.
Final Answer: 6
The compound MX₄ has a tetrahedral geometry. In a tetrahedral shape, the central atom (M) is surrounded by four identical atoms (X) at the corners of a tetrahedron.
In the compound MX₄:
- M is the central atom.
- There are four X atoms surrounding M.
Each pair of X atoms forms an angle with the central atom M. Since there are four X atoms, we can calculate the number of unique XMX angles formed.
- The number of ways to choose 2 X atoms from 4 is given by the combination formula C(n, r), where n is the total number of atoms and r is the number of atoms to choose.
C(4,2)=4!2!(4−2)!=4×32×1=6
The total number of XMX angles formed in the tetrahedral compound MX₄ is 6.
Topper's Solved these Questions
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - assertion and reason
5 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - more than may be correct
2 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Match the column
7 Videos
- Periodic Table BOOK - ALLENCHAPTER - Periodic Table EXERCISE - All Questions
40 Videos
- REACTION MECHANISM (PART-I)BOOK - ALLENCHAPTER - REACTION MECHANISM (PART-I)EXERCISE - MCQ
21 Videos
Similar Questions
Knowledge Check
The number of all the possible stereoisomers formed by the given compound is :
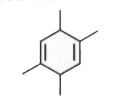 A2B3C32D64
A2B3C32D64Total number of stereoisomers of the compound 2-4-dichloroheptane is:
A0B1C2D3
Alkali metals forms following compound
View Solutionwhich forms interstitial compounds?
View SolutionA mineral MX2 crystallizes in ccp of M2+ ions whereas X− ions occupy the tetrahedral voids. The number of cations and anions per unit cell, the coordination number of cation and percent of tetrahedral voids occupied are :
View SolutionThe compound AgF2 is an unstable compound. However, if formed, the compound acts as a strong oxidising agent. Why?
View SolutionThe correct IUPAC numbering in the compound
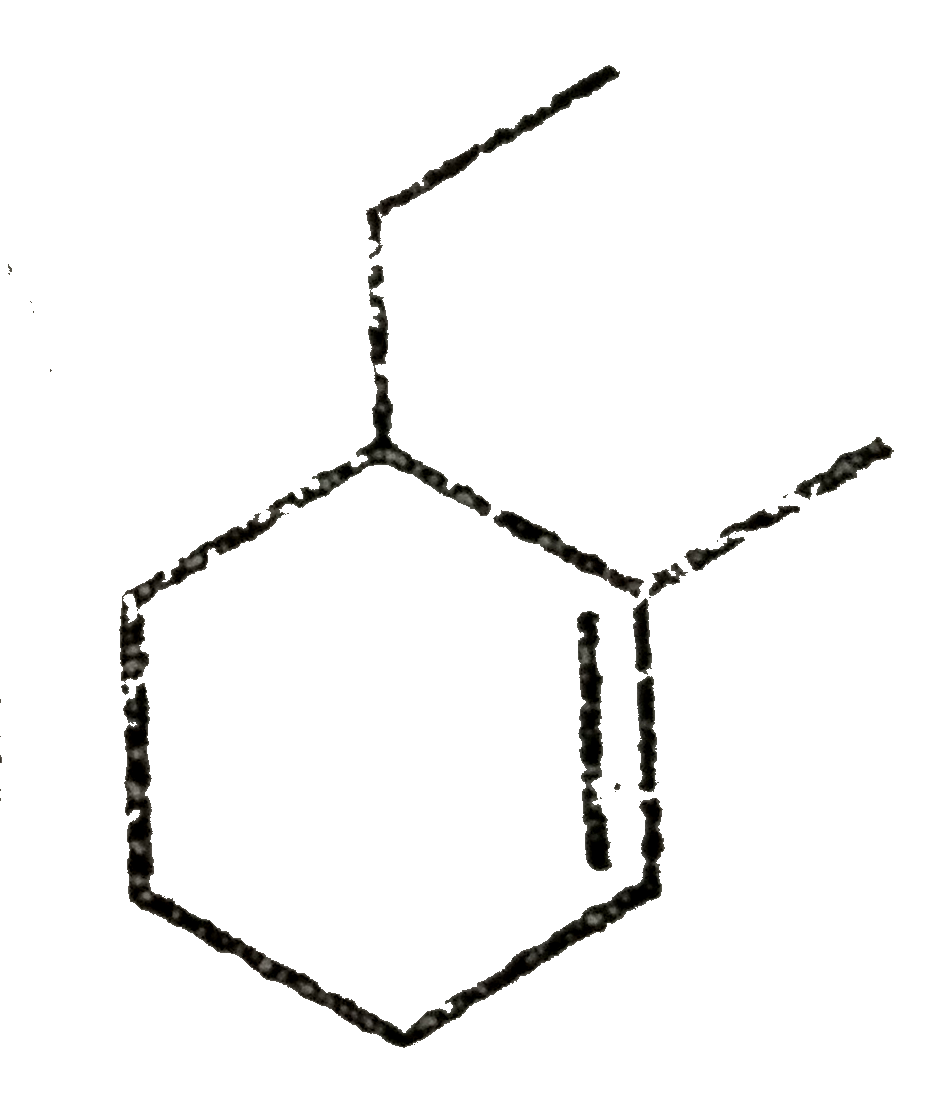 is:
is:
View SolutionWhy Be generally form covalent compounds?
View Solution
