A particle moves in a straight line with a uniform acceleration a. Initial velocity of the particle is zero. Find the average velocity of the particle in first 's' distance.
To solve the problem step by step, we will use the equations of motion under uniform acceleration.
Step 1: Write down the known values
- Initial velocity (u) = 0 (the particle starts from rest)
- Acceleration (a) = a (given)
- Distance (s) = s (the distance we want to find the average velocity over)
Step 2: Use the equation of motion
The equation of motion that relates distance, initial velocity, acceleration, and time is:
s=ut+12at2
Since the initial velocity u=0, the equation simplifies to:
s=12at2
Step 3: Rearrange the equation to find time (t)
From the equation s=12at2, we can solve for time t:
t2=2sa
Taking the square root of both sides gives:
t=√2sa
Step 4: Calculate the average velocity
The average velocity Vavg is defined as the total distance traveled divided by the total time taken:
Vavg=st
Substituting the expression for t from Step 3:
Vavg=s√2sa
Step 5: Simplify the expression
To simplify Vavg:
Vavg=s⋅√a2s
This can be simplified further:
Vavg=√as2
Final Answer
The average velocity of the particle over the first distance s is:
Vavg=√as2
---
- Initial velocity (u) = 0 (the particle starts from rest)
- Acceleration (a) = a (given)
- Distance (s) = s (the distance we want to find the average velocity over)
The equation of motion that relates distance, initial velocity, acceleration, and time is:
s=ut+12at2
Since the initial velocity u=0, the equation simplifies to:
s=12at2
From the equation s=12at2, we can solve for time t:
t2=2sa
Taking the square root of both sides gives:
t=√2sa
The average velocity Vavg is defined as the total distance traveled divided by the total time taken:
Vavg=st
Substituting the expression for t from Step 3:
Vavg=s√2sa
To simplify Vavg:
Vavg=s⋅√a2s
This can be simplified further:
Vavg=√as2
The average velocity of the particle over the first distance s is:
Vavg=√as2
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - EXERCISE-0237videos
MOTION IN A PALNE
- BOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - EXERCISE-036videos
MOTION IN A PALNE
- BOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)46videos
KINEMATICS-2D
- BOOK - ALLENCHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (JA)4videos
NEWTON'S LAWS OF MOTION & FRICTION
Similar Questions
A particle moves on a straight line with a uniform velocity. It's angular momentum
View SolutionThe acceleration-displacement graph of a particle moving in a straight line is as shown in figure, initial velocity of particle is zero. Find the velocity of the particle when displacement of the particle is s=12m.
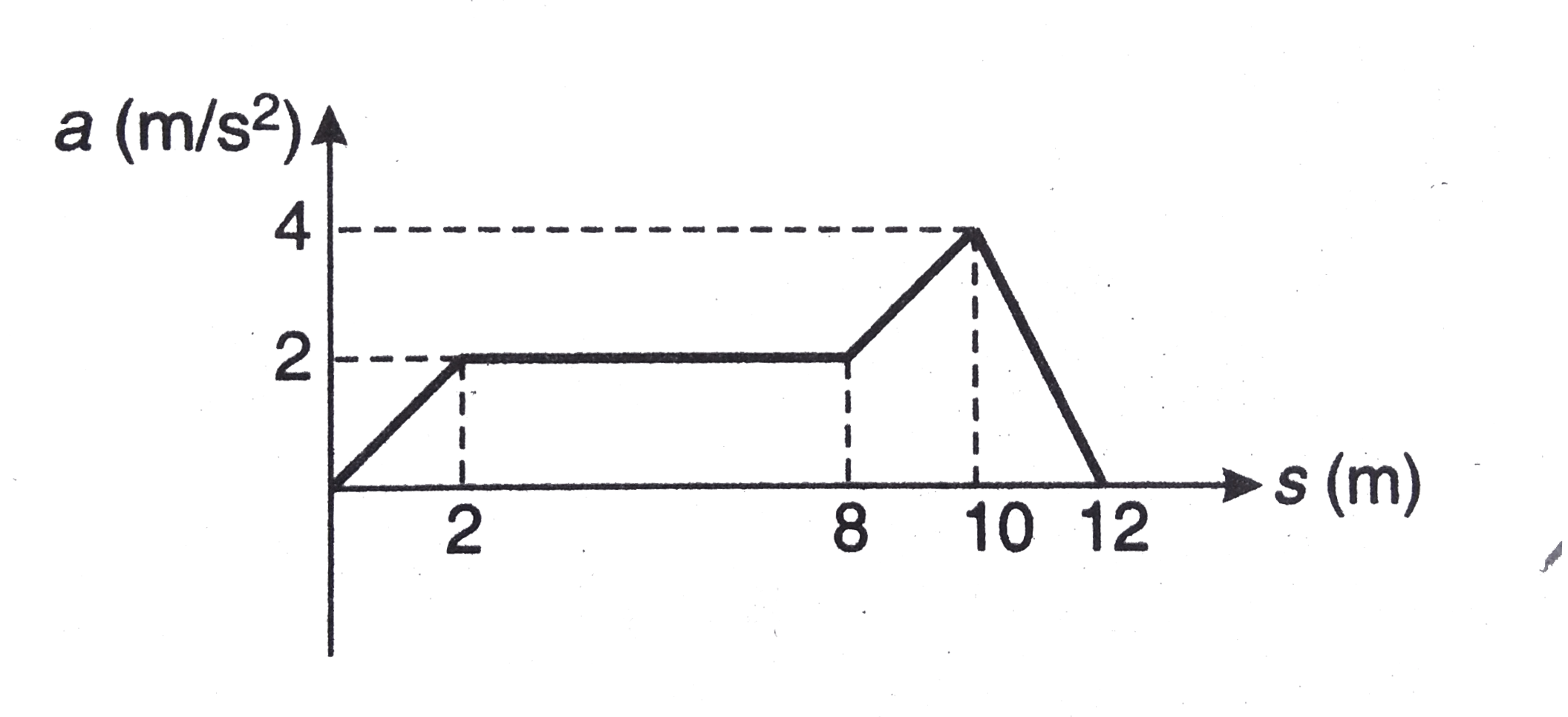 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Acceleration (a)-displacement(s) graph of a particle moving in a straight line is shown here. The initial velocity of the particle is zero. The v-s graph of the particle would be
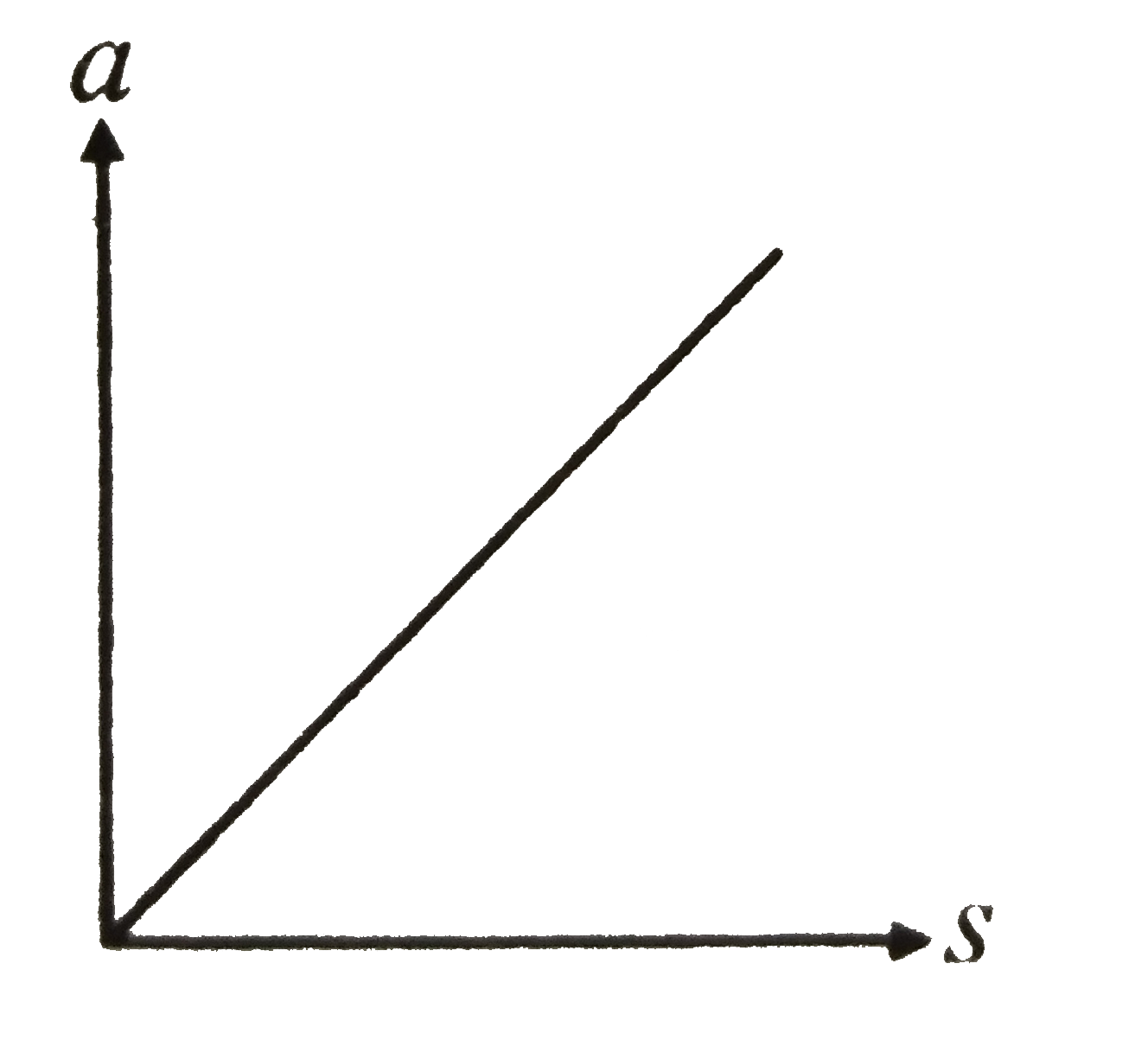 A
A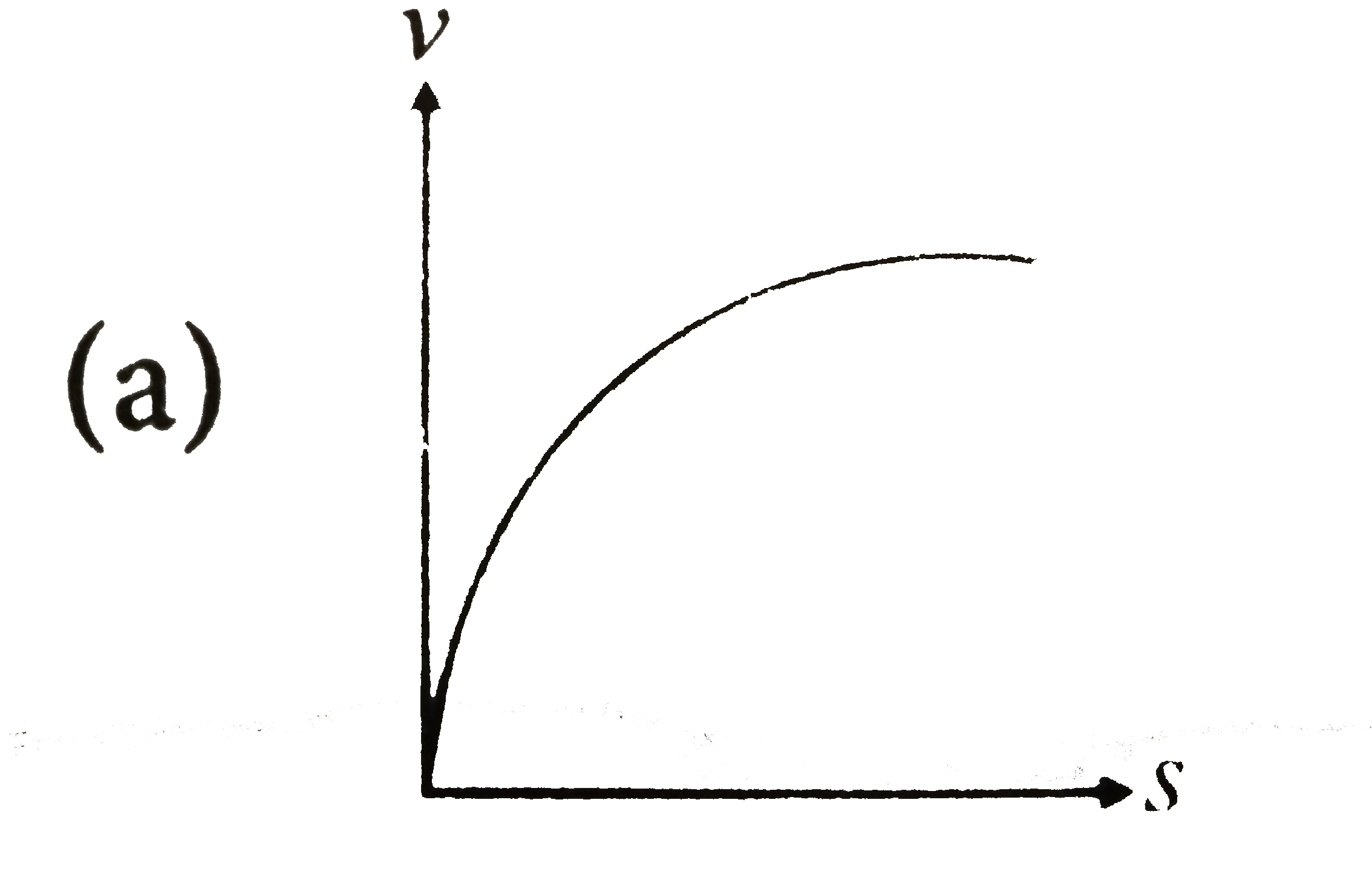 B
B C
C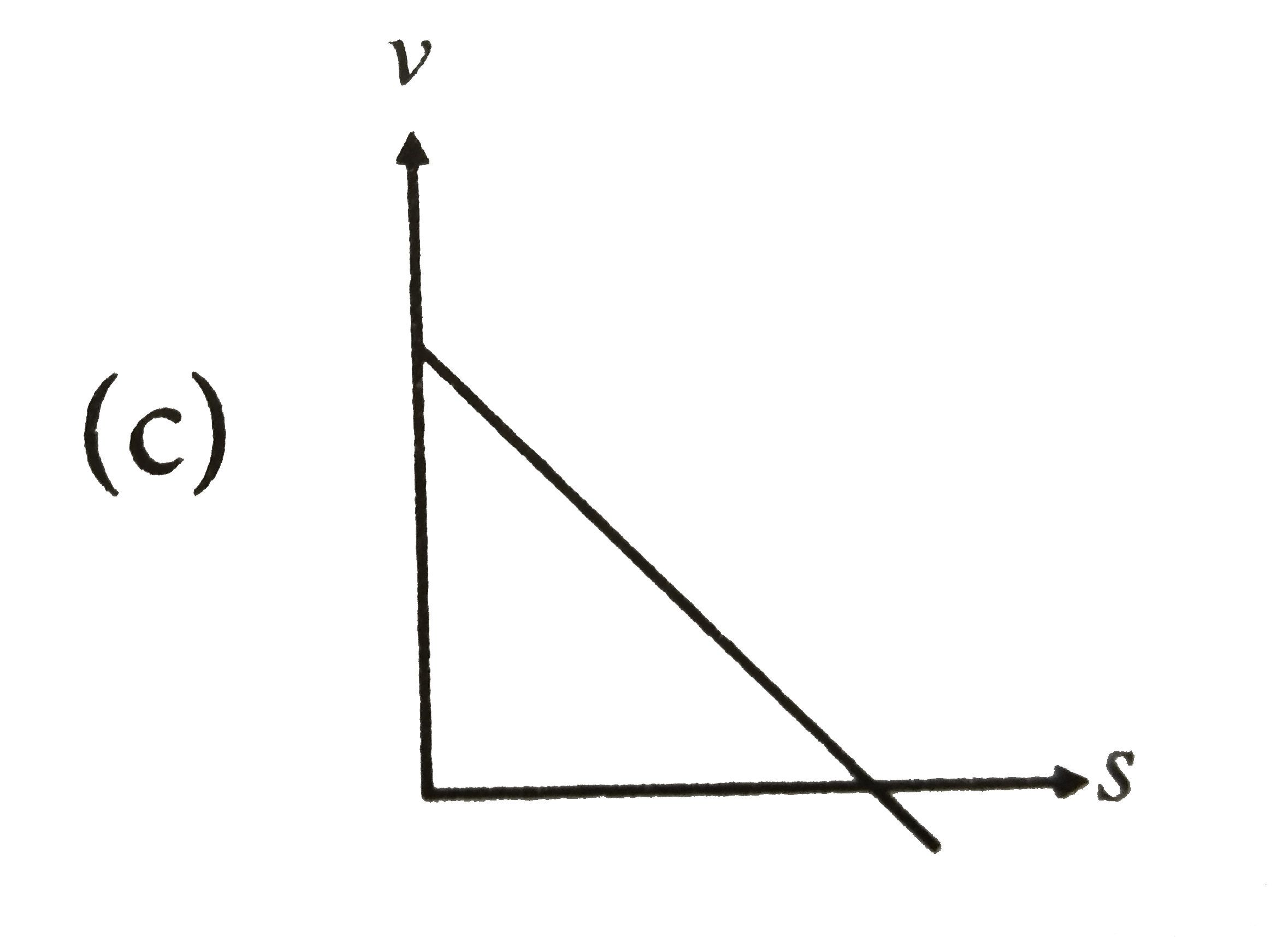 D
D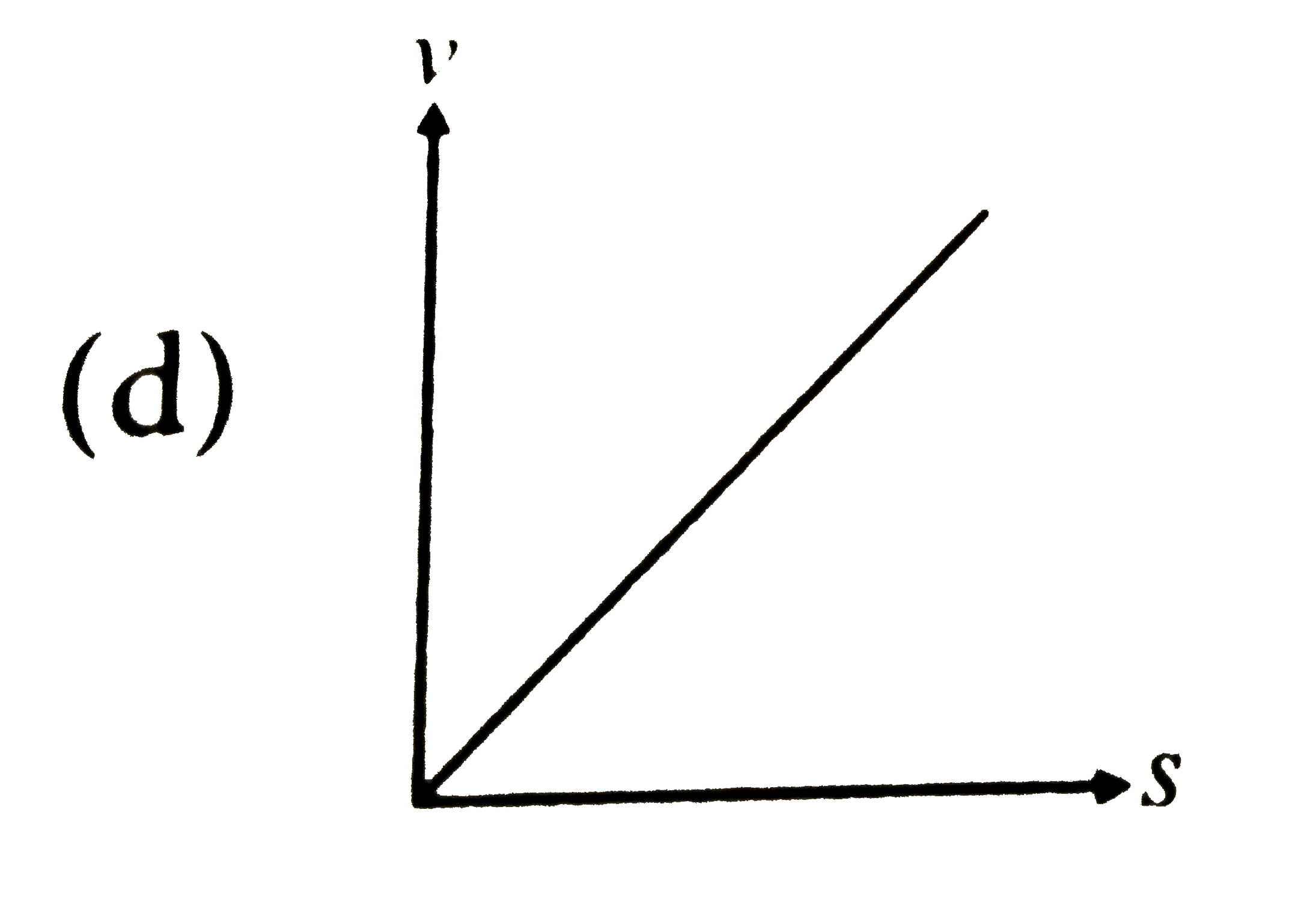
Acceleration (a) -displacement (s) graph of a particle moving in a straight line is as shown in the figure. The initial velocity of the particle is zero. The v−s graph of the particle would be
 View Solution
View SolutionAcceleration of two identical particles moving in a straight line are as shown in figure.
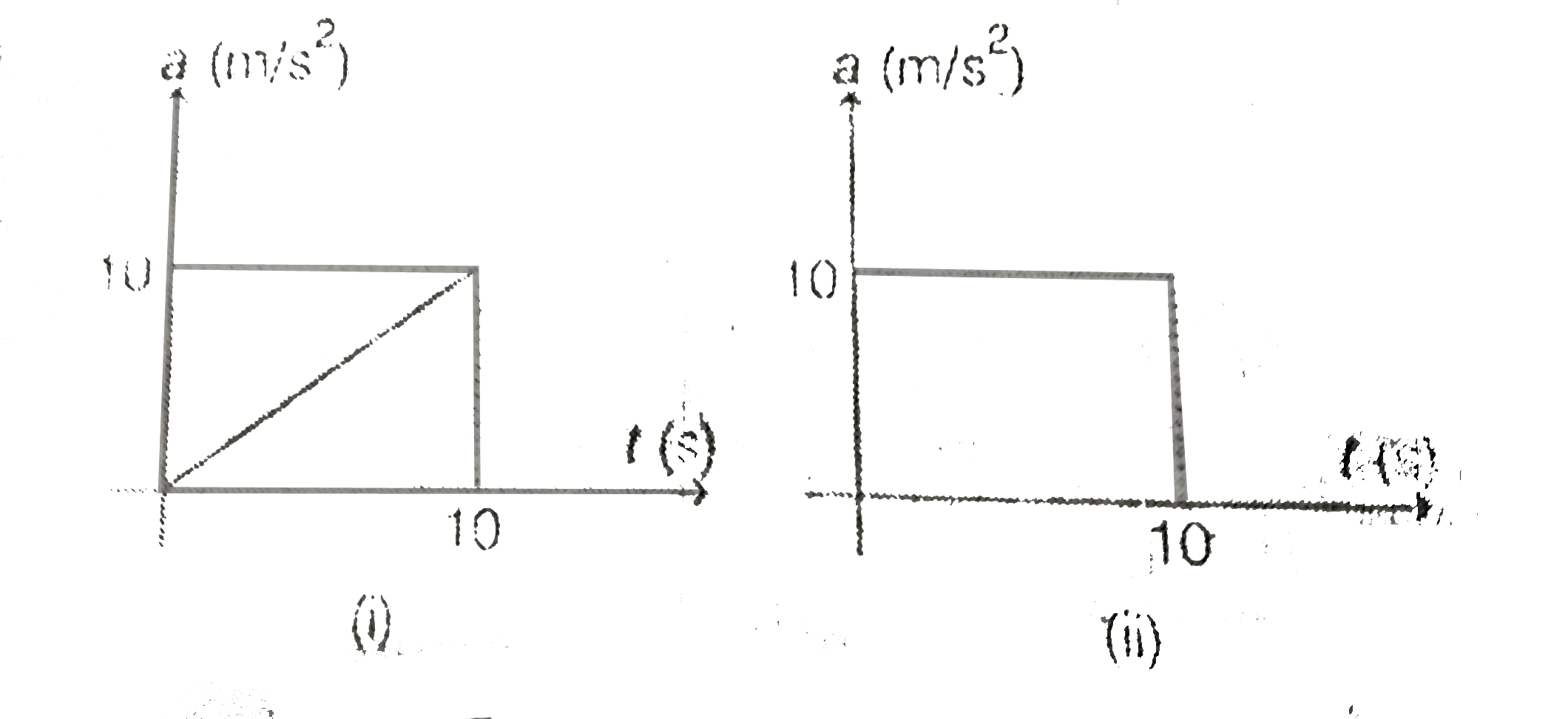
If initial velocity of both the particles was zero. Then velocity of their centre of mass after 10 s will beView Solutionvelocity-time graph of a particle moving in a straight line is as shown in figure. At time t=0, velocity of the particle is zero. Find

(a) average acceleration in a time interval from t=6s to t=12s,
(b) velocity of the particle at t=14s.View SolutionStatement-I : A particle moves in a straight line with constant acceleration. The average velocity of this particle cannot be zero in any time interval.
Statement-II : For a particle moving in straight line with constant acceleration, the average velocity in a time interval is u+v2, where u and v are initial and final velocity of the particle of the given time interval.View SolutionA particle moving along a straight line with uniform acceleration has velocities 7m/s at A and 17m/s at C. B is the mid point of AC. Then :-
View SolutionA particle moves in straight line. Acceleration of particle changes with velocity as showns in graph:
 View Solution
View SolutionA particle starts from rest at t=0 and moves in a straight line with an acceleration as shown below. The velocity of the particle at t=3 s is
 View Solution
View Solution

