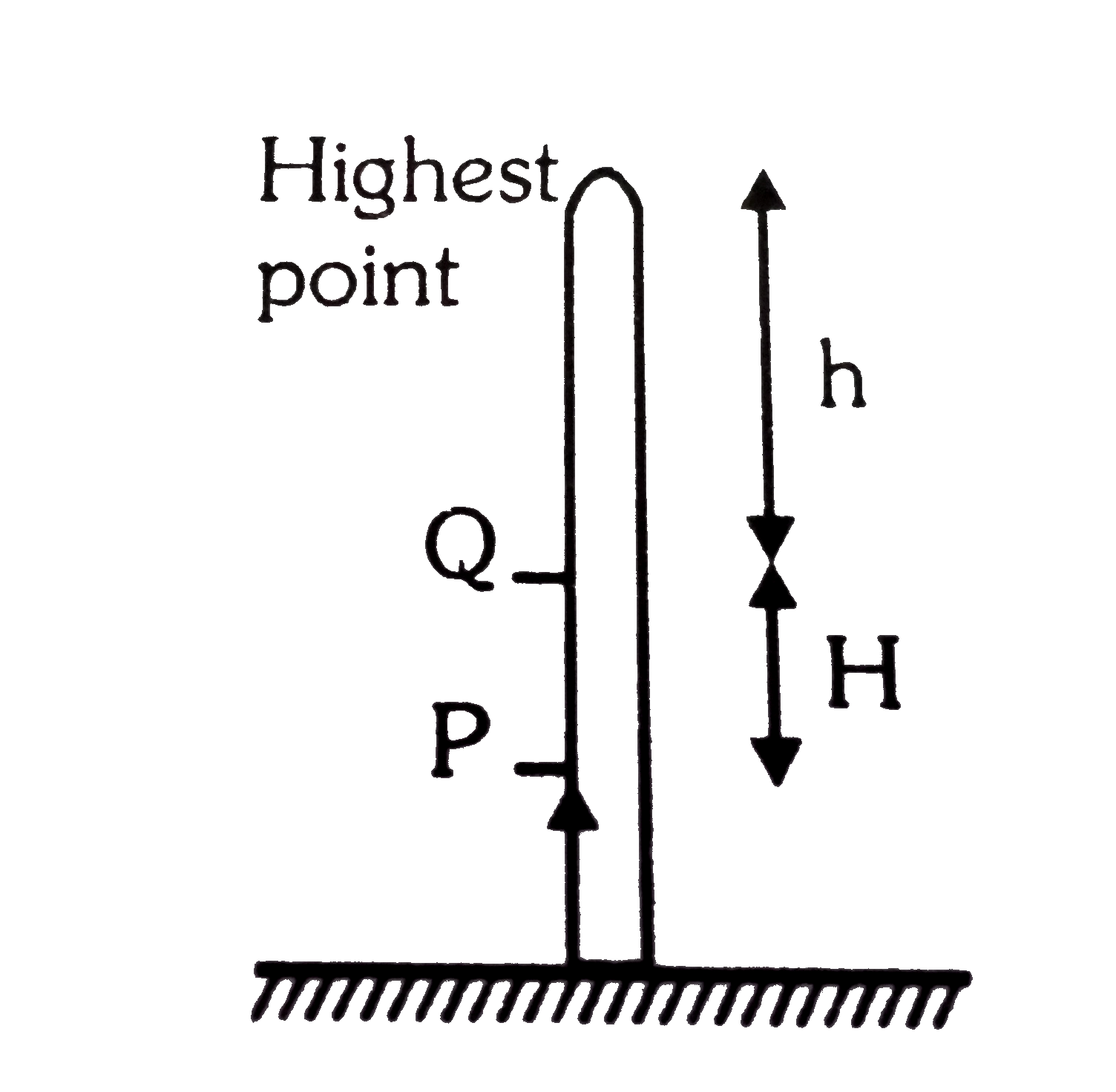
A particle is thrown vertically upwards from the surface of the earth. Let Tp be the time taken by the particle to travel from a point P above the earth to its highest point and back to the point P. Similarly, let TQ be the time taken by the particle to travel from another point Q above the earth to its highest point and back to the same point Q above the earth to tis highest point and back to the same Q. If the distance between the points P and Q is H, find the expression for acceleration due to gravity in terms of TP,TQ and H.
Time taken from point P to point P TP=2√2(h+H)g
Time taken from point Q to point Q TQ=2√2hg
⇒T2p=8(h+H)g&T2Q=8hg⇒T2P=T2Q+8Hg
⇒g=8HT2P−T2Q
Topper's Solved these Questions
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - EXERCISE-1
99 Videos
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - EXERCISE-2
170 Videos
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - Integer Type Question
3 Videos
- KINEMATICS-2DBOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)
46 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLENCHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (JA)
4 Videos
Similar Questions
A particle is thrown vertically upwards from the surface of the earth. Let TP be the time taken by the particle to travel from a point P above the earth to its highest point and back to the point P. Similarly, let TQ be the time taken by the particle to travel from another point Q above the earth to its highest point and back to the same in terms of TP,TQ and H, is :-
View SolutionA particle falls freely near the surface of the earth. Consider a fixed point O (not vertically below the particle) on the ground.
View Solution
Knowledge Check
The time taken by light to travel from sun to earth is approximately
A8 light yearsB8 secondsC8 minutesD8 hoursFrom a tower of height H, a particle is thrown vertically upwards with a speed u. The time taken by the particle, to hit the ground, is n times that taken by it to reach the highest point of its path. The relation between H, u and n is:
AgH = (n−2)u2B2 gH = n2u2CgH = (n−2)2u2D2 gH = ν2(n−2)The point on the surface of the earth vertically above the point of origin of the earthquake is
AEpicentreBFaultCHypocentreDSeismic
A particle is projected vertically upwards from ground with velocity 10 m/s. Find the time taken by it to reach at the highest point ?
View SolutionFrom a tower of height H, a particle is thrown vertically up with a speed V. The time taken by the particle to hit the ground 3 tiem that taken by it to reach the highest point of is path . Then find H.
View SolutionFrom a tower of height H, a particle is thrown vertically upwards with a speed u. The time taken by the particle, to hit the ground, is n times that taken by it to reach the highest point of its path. The relation between H, u and n is
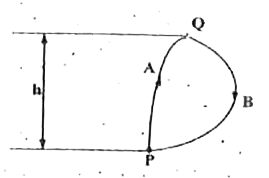
View SolutionA particle is taken from point P to point Q via the path PAQ and then placed back to point P via the path QBP. Find the work done by gravity on the body over this closed path. Vertical separation between P and Q is h as shown.
View SolutionA particle is given a velocity ve√3 in a vertically upward direction from the surface of the earth, where ve is the escape velocity from the surface of the earth. Let the radius of the earth be R. The height of the particle above the surface of the earth at the instant it comes to rest is :
View Solution
