A car starts from erest accelerates uniform by for 4 second and then moves with uniform velocity which of the x-t graph represent th motion of the car:-
The correct Answer is:(i) 20 m (ii) 5s
To solve the problem of determining which x-t graph represents the motion of a car that starts from rest, accelerates uniformly for 4 seconds, and then moves with uniform velocity, we can follow these steps:
Step 1: Understand the Motion Phases
The car has two distinct phases of motion:
1. Acceleration Phase: The car accelerates uniformly from rest for 4 seconds.
2. Constant Velocity Phase: After 4 seconds, the car moves with a constant velocity.
Step 2: Analyze the Acceleration Phase
During the first phase (0 to 4 seconds):
- The car starts from rest, which means its initial velocity (u) is 0.
- It accelerates uniformly, so we can denote the acceleration as 'a'.
- The displacement (x) during this phase can be calculated using the equation of motion:
x=ut+12at2
Since u=0:
x=12at2
This equation represents a parabolic curve on the x-t graph, starting from the origin (0,0).
Step 3: Determine the Velocity After 4 Seconds
At the end of the acceleration phase (t = 4 seconds), we can find the final velocity (v) using:
v=u+at
Substituting u=0:
v=a⋅4=4a
This velocity will remain constant during the second phase of motion.
Step 4: Analyze the Constant Velocity Phase
During the second phase (after 4 seconds):
- The car moves with a constant velocity of 4a.
- The displacement can be expressed as:
x=x0+vt
where x0 is the displacement at t=4 seconds, and v=4a.
Step 5: Combine Both Phases on the x-t Graph
1. From t=0 to t=4: The graph will be a parabolic curve starting from the origin (0,0).
2. From t=4 onwards: The graph will be a straight line with a positive slope, representing constant velocity.
Conclusion
The x-t graph will start at the origin, curve upwards (parabola) for the first 4 seconds, and then transition into a straight line with a constant slope after 4 seconds.
The car has two distinct phases of motion:
1. Acceleration Phase: The car accelerates uniformly from rest for 4 seconds.
2. Constant Velocity Phase: After 4 seconds, the car moves with a constant velocity.
During the first phase (0 to 4 seconds):
- The car starts from rest, which means its initial velocity (u) is 0.
- It accelerates uniformly, so we can denote the acceleration as 'a'.
- The displacement (x) during this phase can be calculated using the equation of motion:
x=ut+12at2
Since u=0:
x=12at2
This equation represents a parabolic curve on the x-t graph, starting from the origin (0,0).
At the end of the acceleration phase (t = 4 seconds), we can find the final velocity (v) using:
v=u+at
Substituting u=0:
v=a⋅4=4a
This velocity will remain constant during the second phase of motion.
During the second phase (after 4 seconds):
- The car moves with a constant velocity of 4a.
- The displacement can be expressed as:
x=x0+vt
where x0 is the displacement at t=4 seconds, and v=4a.
1. From t=0 to t=4: The graph will be a parabolic curve starting from the origin (0,0).
2. From t=4 onwards: The graph will be a straight line with a positive slope, representing constant velocity.
The x-t graph will start at the origin, curve upwards (parabola) for the first 4 seconds, and then transition into a straight line with a constant slope after 4 seconds.
Topper's Solved these Questions
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - Exercise-04[B]
14 Videos
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - Exercise-05 [A]
11 Videos
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - Comprehension#7
3 Videos
- KINEMATICS-2DBOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)
46 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLENCHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (JA)
4 Videos
Similar Questions
Knowledge Check
A car starts from rest moves with uniform acceleration a1 for t1 second and then retards uniformly at a rate a2 for t2 second. Then t1/t2 is equal to
Aa1/a2Ba2/a1Ca22/a1D2a1/a2
A body starts from rest and then moves with uniform acceleration. Then.
View SolutionA car starts from rest and moves with uniform acceleration for time t then it moves with uniform speed of 60 km/h for time 3t and comes to rest. Find the average speed of car in its total journey.
View SolutionWhich of the following velocity-time graphs represent uniform motion
View SolutionA body moves for a total of nine second starting from rest with uniform acceleration and then with uniform retardation, which is twice the value of acceleration and then stop. The duration of uniform acceleration is
View SolutionAs soon as a car just starts from rest in a certain dercation, a scooter moveing with a uniform speed overtakes the car. Their velocity-time graph is shown in . Calculate
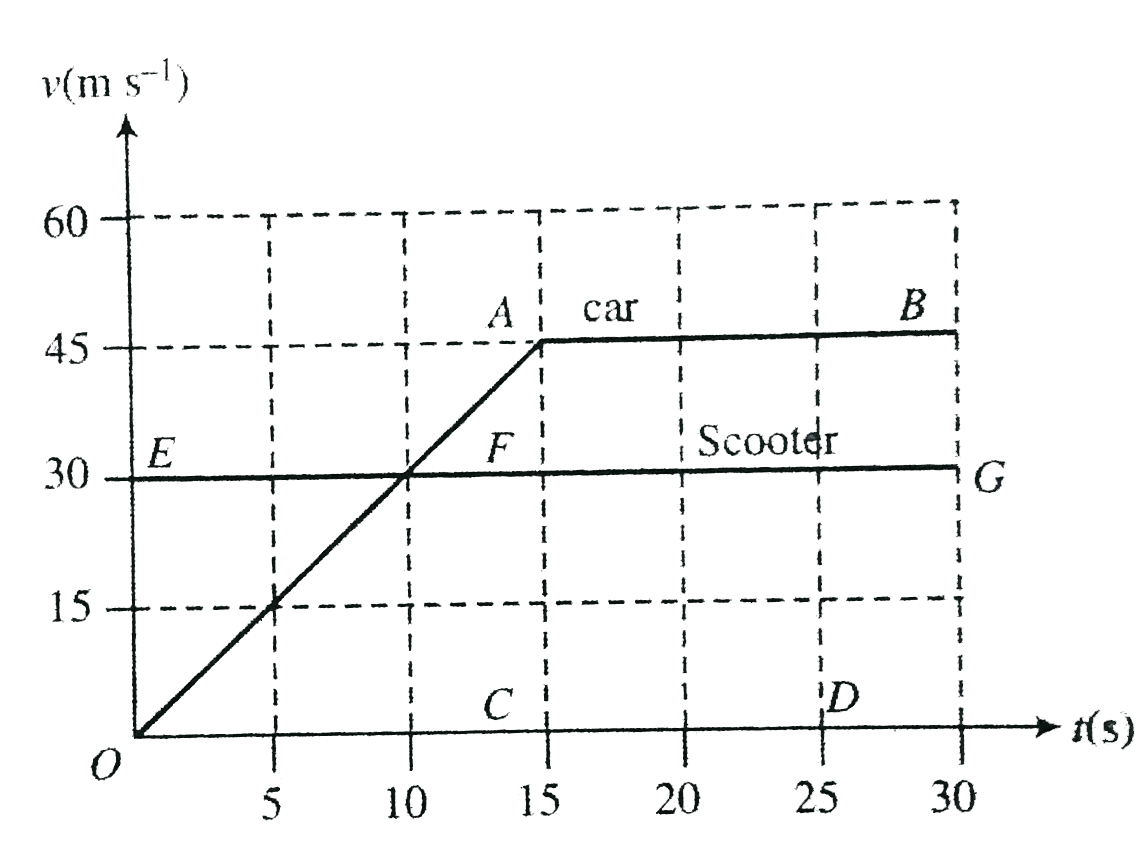 .
.
a. The difference between the distances travlled by the car and the scooter in 15s,
b. The distance of car and scooter from the starting point at that instant.
View SolutionThe speed-time graph for a car is shown is Figure

(a) Find how far does the car travel in the first 4 seconds. Shade the area on the graph that represents the distance travelled by the car during this period.
(b) Which part of the graph represents uniform motion of the car ?
View SolutionA body starts from rest and moves with a uniform acceleration of 10ms−2 for 5 seconds. During the next 10 seconds it moves with uniform velocity. Find the total distance travelled by the body (Using graphical analysis).
View Solution
