The thermo emf of a thermocouple is given by Determine the neutral temperature and inversion temperature.
To solve the problem of determining the neutral temperature and inversion temperature from the given thermo emf equation of a thermocouple, we can follow these steps:
1. Understand the Given Equation:
The thermo emf E of a thermocouple is given by:
E=α(θ−θg)+β(θ2−θ20)
where α and β are constants, θ is the temperature, θg is a reference temperature, and θ0 is another reference temperature.
2. Determine the Neutral Temperature:
The neutral temperature (θn) is defined as the temperature at which the derivative of E with respect to θ is zero:
dEdθ=0
- Differentiate E with respect to θ:
dEdθ=α+2βθ
- Set the derivative equal to zero:
α+2βθ=0
- Solve for θ:
2βθ=−α⟹θ=−α2β
Thus, the neutral temperature is:
θn=−α2β
3. Determine the Inversion Temperature:
The inversion temperature (θi) is defined as the temperature at which the emf E is zero:
E=0
- Set the equation for E to zero:
0=α(θ−θg)+β(θ2−θ20)
- Rearranging gives:
α(θ−θg)=−β(θ2−θ20)
- Factor out (θ−θ0)(θ+θ0):
α(θ−θg)=−β(θ−θ0)(θ+θ0)
- Setting θ−θ0=0 gives one solution:
θ=θ0
- For the other solution, divide both sides by (θ−θ0):
α=−β(θ+θ0)⟹θ+θ0=−αβ
θi=−αβ−θ0
Thus, the inversion temperature is:
θi=−αβ−θ0
Final Answers:
- Neutral Temperature: θn=−α2β
- Inversion Temperature: θi=−αβ−θ0
The thermo emf E of a thermocouple is given by:
E=α(θ−θg)+β(θ2−θ20)
where α and β are constants, θ is the temperature, θg is a reference temperature, and θ0 is another reference temperature.
The neutral temperature (θn) is defined as the temperature at which the derivative of E with respect to θ is zero:
dEdθ=0
dEdθ=α+2βθ
α+2βθ=0
2βθ=−α⟹θ=−α2β
θn=−α2β
The inversion temperature (θi) is defined as the temperature at which the emf E is zero:
E=0
0=α(θ−θg)+β(θ2−θ20)
α(θ−θg)=−β(θ2−θ20)
α(θ−θg)=−β(θ−θ0)(θ+θ0)
θ=θ0
α=−β(θ+θ0)⟹θ+θ0=−αβ
θi=−αβ−θ0
θi=−αβ−θ0
- Neutral Temperature: θn=−α2β
- Inversion Temperature: θi=−αβ−θ0
Similar Questions
When the cold junction of a thermocouple is maintained at 0∘C, the thermo em .e., generated by this thermocouple is given by the relation
e=[16⋅8+12(−0⋅0480)θ2]×10−6
where θ is the temperature of the hot junction in ∘C. Find the neutral temperature of this thermocouple.
View SolutionAbove neutral temperature, thermo e.m.f. in a thermocouple
View SolutionIntegrate the following functions
∫θ2θ1dθθ−θ0
View SolutionShow, with the help of a labelled graph, how thermo emf .e. developed by a thermocouple varies with θ, the temperature difference between the two junctions. On the graph, mark neutral temperature as θN and temperature of inversion as θ1.
View SolutionThe thermo emf E of a thermocouple is found to vary wit temperature T of the junction (cold junction is 0∘C) as
E=40T−T220
The temperature of inversion for the thermocouple is
View SolutionTwo materials having coefficients of thermal conductivity '3k' and 'k' and thickness 'd' and '3d' respectively, are joined to form a slab as shown in the figures. The temperatures of the outer surfaces are θ2 and θ1 respectively (θ2>θ2). The temperature at the interface is :
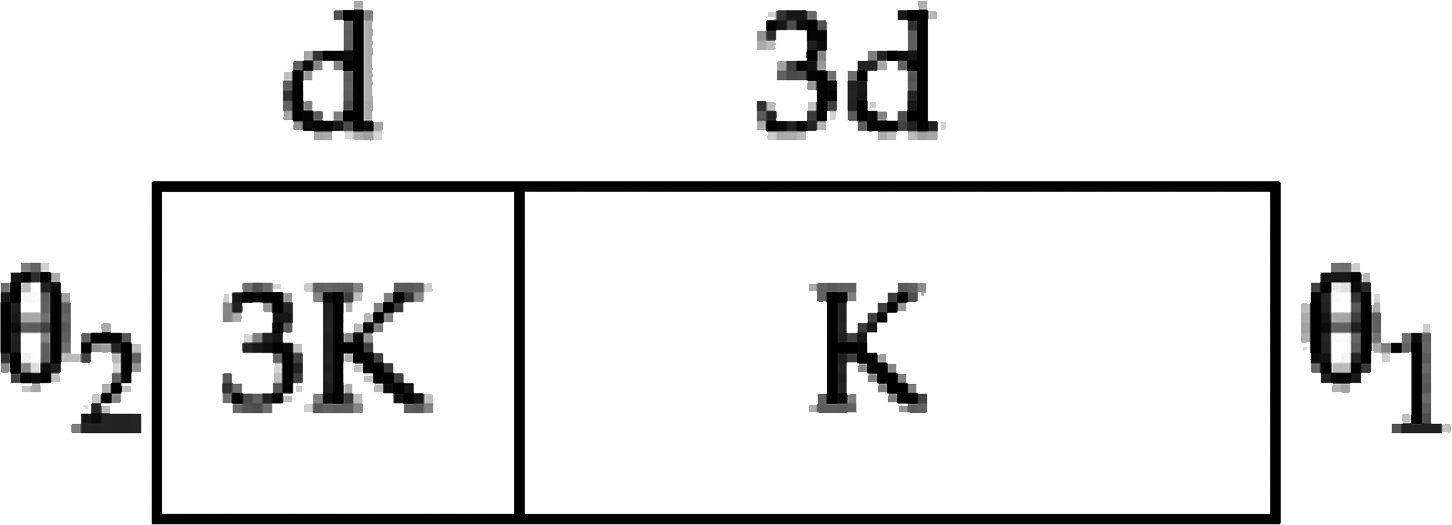
View SolutionPlot a labelled graph to show variation of thermo-emf .e. versus temperature difference .θ. between the two junctions of a thermocouple. Mark .N. as neutral temperature and I as temperature of inversion.
(ii) What is Peltier effect ?
View SolutionThermo e.m.f. E of a Cu-Fe thermocouple varies with the temperature θ of the hot junction ( cold juction 0∘C) as E(μV)=12θ−0.02θ2.
Determine:-
(a) Neutral temperature of the termocouple
(b) Temperature of inversion, assuming that cold junction is at 20∘C.
(c) Value of Seebeck coefficient at neutral temperature
View SolutionThe emf ɛ of a Cu-Fe thermocouple varies with the temperature θ of the hot junction (cold junction at 0∘C ), as ɛ(μV)=14θ−0.02θ2 Determine the neutral temperature.
View SolutionThe rate of increase of thermo-emf with temperature at the neutral temperature of a thermocouple
View Solution
