If the potential difference across the ends of a conductor is doubled, the energy loss becomes-
double
4 times
8 times
14 times
To solve the problem, we need to analyze how the energy loss in a conductor changes when the potential difference across its ends is doubled.
1. Understand the relationship between power, voltage, and resistance:
The power (P) dissipated in a resistor due to a potential difference (V) is given by the formula:
P=V2R
where R is the resistance of the conductor.
2. Initial power (energy loss):
Let's denote the initial potential difference as V. Therefore, the initial power (or energy loss) can be expressed as:
P=V2R(Equation 1)
3. Doubling the potential difference:
If the potential difference is doubled, the new potential difference V′ becomes:
V′=2V
4. Calculate the new power (energy loss):
Now, we can calculate the new power (or energy loss) when the potential difference is V′:
P′=(V′)2R=(2V)2R
Simplifying this gives:
P′=4V2R(Equation 2)
5. Compare the new power with the initial power:
From Equation 1, we know that P=V2R. Now, substituting this into our expression for P′:
P′=4(V2R)=4P
6. Conclusion:
Therefore, when the potential difference across the ends of the conductor is doubled, the energy loss becomes four times the initial energy loss.
Final Answer:
The energy loss becomes 4 times the initial energy loss.
---
The power (P) dissipated in a resistor due to a potential difference (V) is given by the formula:
P=V2R
where R is the resistance of the conductor.
Let's denote the initial potential difference as V. Therefore, the initial power (or energy loss) can be expressed as:
P=V2R(Equation 1)
If the potential difference is doubled, the new potential difference V′ becomes:
V′=2V
Now, we can calculate the new power (or energy loss) when the potential difference is V′:
P′=(V′)2R=(2V)2R
Simplifying this gives:
P′=4V2R(Equation 2)
From Equation 1, we know that P=V2R. Now, substituting this into our expression for P′:
P′=4(V2R)=4P
Therefore, when the potential difference across the ends of the conductor is doubled, the energy loss becomes four times the initial energy loss.
The energy loss becomes 4 times the initial energy loss.
Similar Questions
If the potential difference across the ends of a conductor is doubled, the current flowing through it gets
View SolutionFind the potential difference across C2.
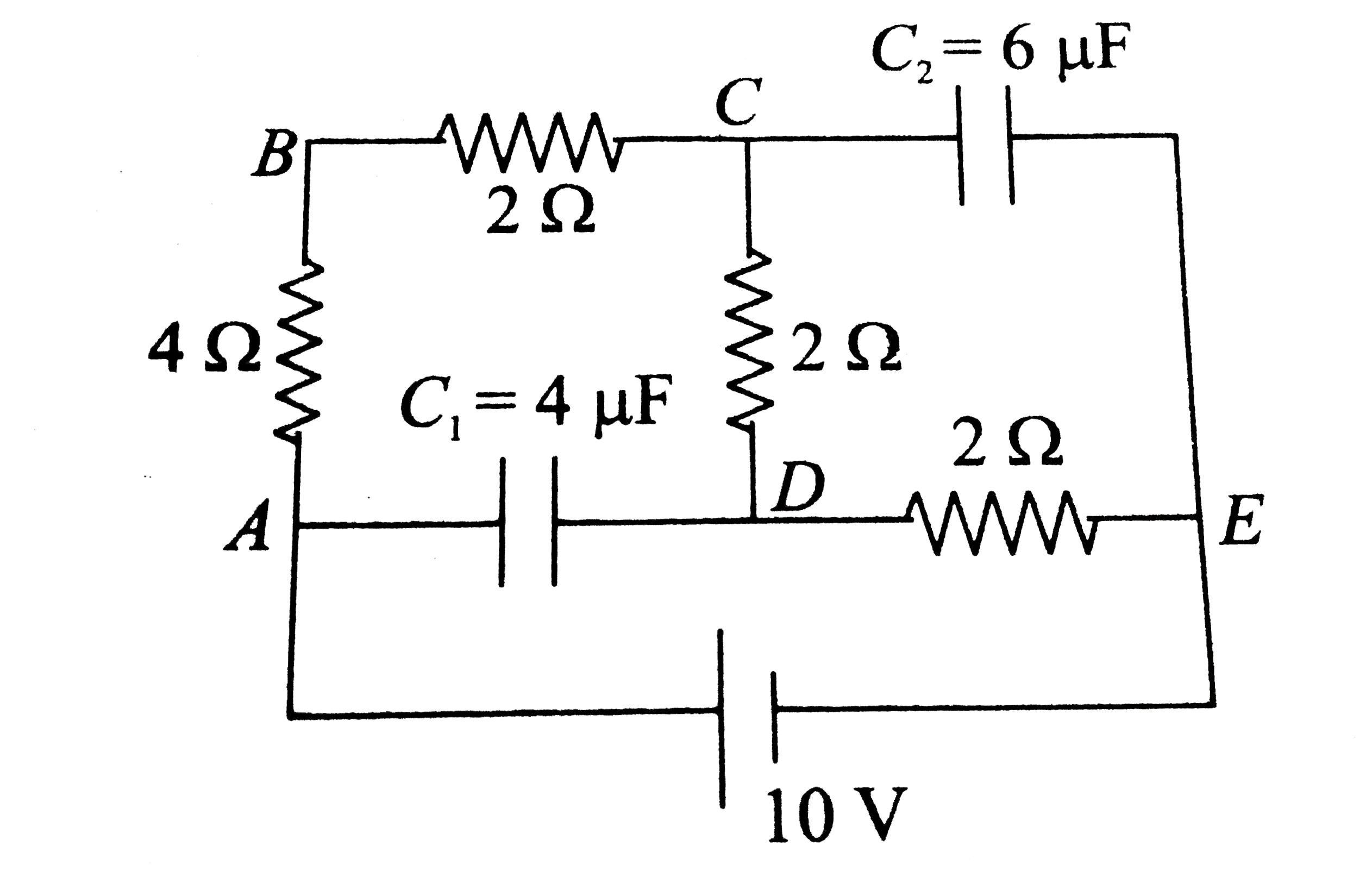
View SolutionHow does the mobility of electrons in a conductor change, if the potential difference applied across the conductor is doubled, keeping the length and temperature of the conductor constant ?
View SolutionThe drift speed of electrons in copper wire of diameter and length l is v . If the potential difference across the wire is doubled, then the new drift speed becomes
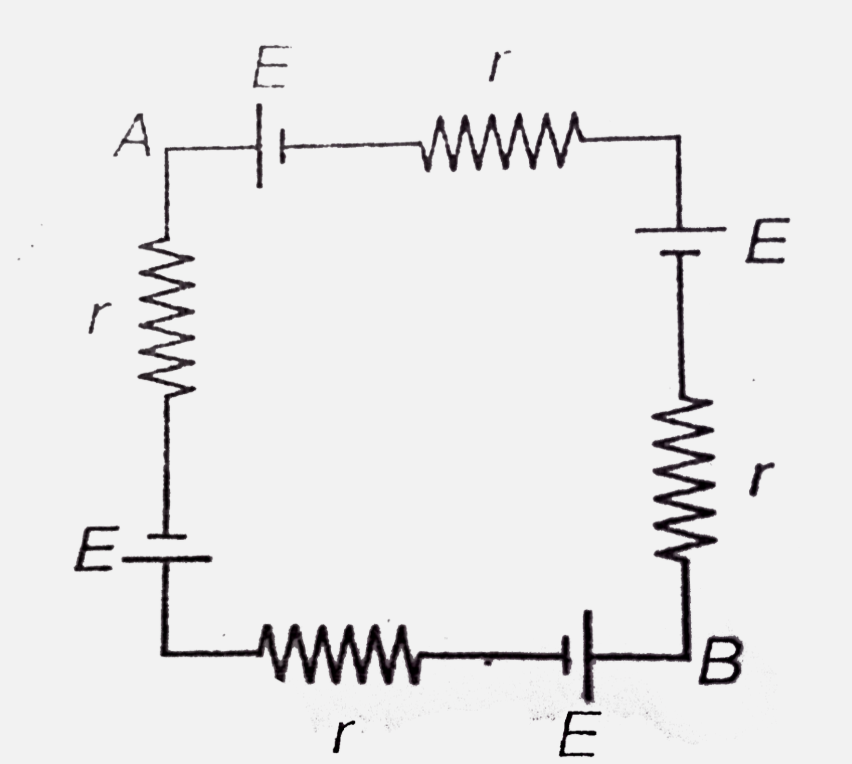
View SolutionPotential difference across AB in the networ shown is
View SolutionPotential difference across the terminal of a non ideal battery is
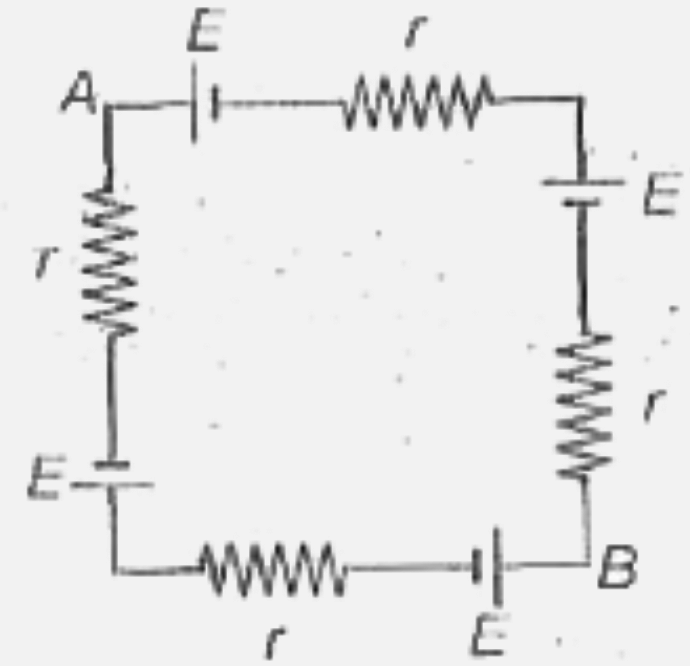
View SolutionPotential difference across AB in the network shown is
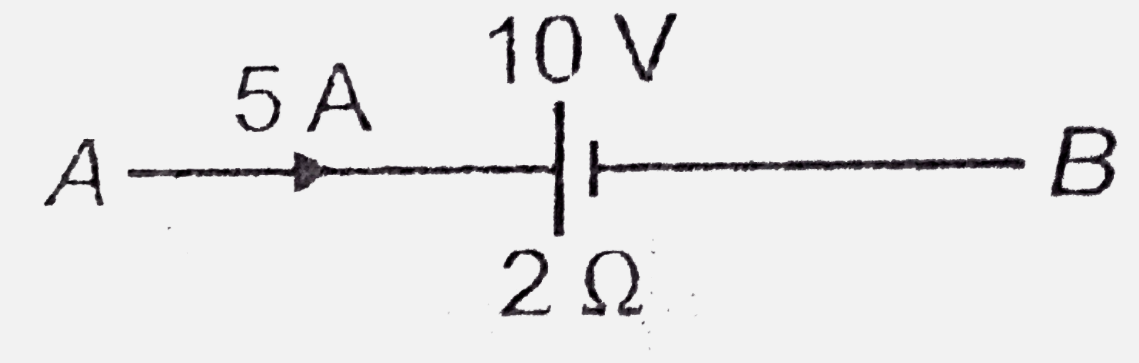
View SolutionPotential difference across AB in the network shown is
View SolutionIf the potential difference applied across a Coolidge tube is increased , then
View SolutionIf the potential difference applied across a Coolidge tube is increased , then
View Solution
