The electrochemical equivalent of a substance is numerically equal to the mass of the substance deposited if a current 1 flows through the electrolyte for 0.25 seconds. The value of 1 is
a) 1A
b) 2A
c) 3A
d) 4A
To solve the problem, we will use Faraday's first law of electrolysis, which states that the mass (M) of a substance deposited during electrolysis is directly proportional to the quantity of electricity (Q) passed through the electrolyte. The relationship can be expressed as:
M=Z⋅I⋅T
Where:
- M = mass of the substance deposited
- Z = electrochemical equivalent of the substance
- I = current in amperes
- T = time in seconds
Given in the problem, the electrochemical equivalent of the substance is numerically equal to the mass of the substance deposited. This means:
M=Z
From the equation above, we can substitute M with Z:
Z=Z⋅I⋅T
Now, we can simplify this equation. Since M=Z, we can write:
Z=I⋅T
Now, we need to find the value of I. We know that the time T is given as 0.25 seconds. We can rearrange the equation to solve for I:
I=ZT
Since Z is equal to M (which is numerically equal to the mass deposited), we can assume Z=1 (as it is not specified in the problem). Therefore:
I=10.25
Now, we can calculate I:
I=4amperes
Thus, the value of the current I is 4 amperes.
Summary of Steps:
1. Write down Faraday's first law of electrolysis: M=Z⋅I⋅T.
2. Recognize that M=Z (mass is numerically equal to electrochemical equivalent).
3. Substitute M with Z in the equation: Z=I⋅T.
4. Rearrange to find I: I=ZT.
5. Substitute Z=1 and T=0.25 seconds into the equation: I=10.25.
6. Calculate I: I=4amperes.
- M = mass of the substance deposited
- Z = electrochemical equivalent of the substance
- I = current in amperes
- T = time in seconds
1. Write down Faraday's first law of electrolysis: M=Z⋅I⋅T.
2. Recognize that M=Z (mass is numerically equal to electrochemical equivalent).
3. Substitute M with Z in the equation: Z=I⋅T.
4. Rearrange to find I: I=ZT.
5. Substitute Z=1 and T=0.25 seconds into the equation: I=10.25.
6. Calculate I: I=4amperes.
Similar Questions
The electrochemical equivalent of copper is 0.0003296 g coulomb−1. Calculate the amount of copper deposited by a current of 0.5 ampere following through copper sulphate solution for 50 minutes.
View SolutionThe amount of substance deposited by the passage of 1 A of current for 1s is equal to :
View Solution
Knowledge Check
- Question 1 - Select One
The equivalent energy of 1 g of substance is
A9×1013 JB6×1012 JC3×1013 JD6×1013 J - Question 2 - Select One
Electrochemical equivalent is the amount of substance which gets deposited from its solution on passing electrical charge equal to :
A96,500 coulombB1 coulombC60 coulombD965 coloumb
The current I1 (in A) flowing through the 1Ω resistor in the given circuit is
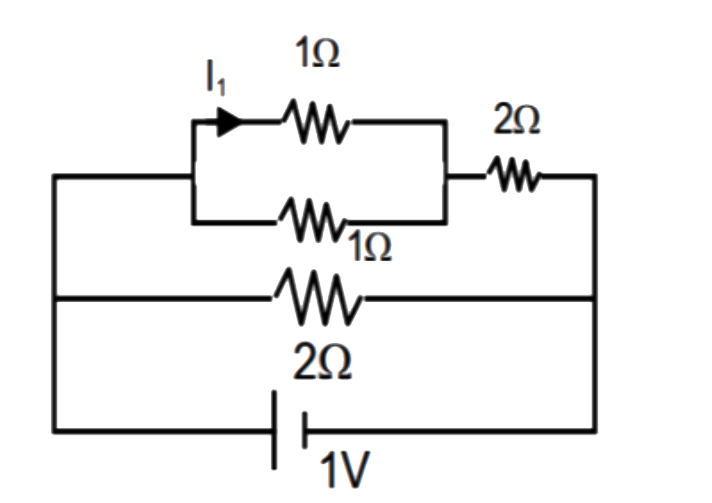 View Solution
View SolutionThe value of the current I1,I2andI3 flowing through the circuit given below is
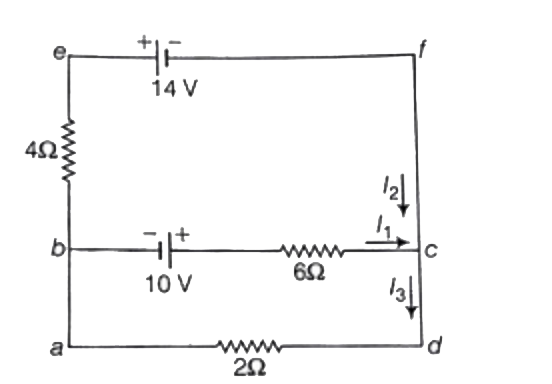 View Solution
View SolutionThe amount of substance liberated when 1 ampere of current is passed for 1 second through an electrolytic solution is called………………… .
View SolutionThe equivalent conductance of a substance is 1/3rd of the molar conductance . The time required to electrolyse 3 moles the substance using a current of 9 ampere is
View SolutionCalculate the energy equivalent of 1g of substance.
View SolutionThe electrochemical equivalent of silver is 0.0011191 g. When an electric current of 0.5 ampere is passed through an aquesus silver nitrate solution of 200 sec, the amount fo silver deposited is:
View Solution

