A hunter is riding an elephant of height 4m moving in straight line with uniform speed of 2m/sec. A deer running with a speed V in front at a distance of 4√5 moving perpendicular to the direction of motion of the elephant. If hunter can throw his spear with a speed of 10m/sec. relative to the elephant, then at what angle θ to it's direction of motion must he throw his spear horizontally for a successful hit. Find also the speed 'V' of the deer.
The correct Answer is:θ=37∘,v=6m/s
To solve the problem step by step, we will analyze the motion of the hunter, the elephant, and the deer.
Step 1: Understanding the scenario
The elephant is moving with a speed of 2m/s in a straight line, and the hunter is at a height of 4m. The deer is running perpendicular to the direction of the elephant's motion at a distance of 4√5m. The spear is thrown at an angle θ with respect to the direction of motion of the elephant.
Step 2: Calculate the time of flight of the spear
The spear is thrown from a height of 4m. The vertical motion of the spear can be described by the equation of motion:
h=12gt2
where h=4m and g=9.8m/s2. Rearranging gives:
4=12⋅9.8⋅t2
t2=89.8≈0.8163
t≈√0.8163≈0.9s
Step 3: Determine the horizontal distance covered by the spear
The horizontal component of the spear's velocity can be expressed as:
vx=velephant+vspear⋅cos(θ)
where velephant=2m/s and vspear=10m/s. The horizontal distance the spear must cover to hit the deer is 4√5m.
Step 4: Set up the equation for horizontal distance
The horizontal distance covered by the spear in time t is given by:
Distance=vx⋅t
Substituting the known values:
4√5=(2+10cos(θ))⋅0.9
Solving for cos(θ):
4√5=(2+10cos(θ))⋅0.9
4√50.9=2+10cos(θ)
Calculating 4√5≈8.944:
8.9440.9≈9.93
9.93=2+10cos(θ)
10cos(θ)=9.93−2=7.93
cos(θ)=7.9310=0.793
Step 5: Calculate the angle θ
Using the cosine value:
θ=cos−1(0.793)≈37∘
Step 6: Find the speed V of the deer
The vertical component of the spear's velocity at the time of hitting the deer must equal the speed of the deer:
V=vspear⋅sin(θ)
Calculating sin(37∘)≈0.6:
V=10⋅0.6=6m/s
Final Answers:
- The angle θ at which the spear must be thrown is approximately 37∘.
- The speed V of the deer is 6m/s.
The elephant is moving with a speed of 2m/s in a straight line, and the hunter is at a height of 4m. The deer is running perpendicular to the direction of the elephant's motion at a distance of 4√5m. The spear is thrown at an angle θ with respect to the direction of motion of the elephant.
The spear is thrown from a height of 4m. The vertical motion of the spear can be described by the equation of motion:
h=12gt2
where h=4m and g=9.8m/s2. Rearranging gives:
4=12⋅9.8⋅t2
t2=89.8≈0.8163
t≈√0.8163≈0.9s
The horizontal component of the spear's velocity can be expressed as:
vx=velephant+vspear⋅cos(θ)
where velephant=2m/s and vspear=10m/s. The horizontal distance the spear must cover to hit the deer is 4√5m.
The horizontal distance covered by the spear in time t is given by:
Distance=vx⋅t
Substituting the known values:
4√5=(2+10cos(θ))⋅0.9
Solving for cos(θ):
4√5=(2+10cos(θ))⋅0.9
4√50.9=2+10cos(θ)
Calculating 4√5≈8.944:
8.9440.9≈9.93
9.93=2+10cos(θ)
10cos(θ)=9.93−2=7.93
cos(θ)=7.9310=0.793
Using the cosine value:
θ=cos−1(0.793)≈37∘
The vertical component of the spear's velocity at the time of hitting the deer must equal the speed of the deer:
V=vspear⋅sin(θ)
Calculating sin(37∘)≈0.6:
V=10⋅0.6=6m/s
- The angle θ at which the spear must be thrown is approximately 37∘.
- The speed V of the deer is 6m/s.
Topper's Solved these Questions
- KINEMATICS-2DBOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-1)
40 Videos
- KINEMATICS-2DBOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)
46 Videos
- KINEMATICS-2DBOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (S-1)
30 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - SOLVED EXAMPLE
28 Videos
Similar Questions
Knowledge Check
In the question number 97, the speed of the child running opposite to the direction of motion of the belt is
A4kmh−1B5kmh−1C9kmh−1D13kmh−1
A bullet is fired with speed 50m/s at 45∘ angle with horizontal. Find the height of the bullet when its direction of motion makes angle 30∘ with the horizontal.
View SolutionA cricket fielder can throw the cricket ball with a speed v0. If the throws the ball while running with speed u at an angle θ to the horizontal,
View SolutionThe wind is blowing due south with speed of 3m/sec. How fast should a car travel due east in order that the wind shall hasve a speed of 5m/sec relative to the car.
View SolutionA sphere of mass m moves with a velocity 2v and collides inelastically with another identical sphere of mass m. After collision the first mass moves with velocity v in a direction perpendicular to the initial direction of motion . Find the speed of the second sphere after collision .
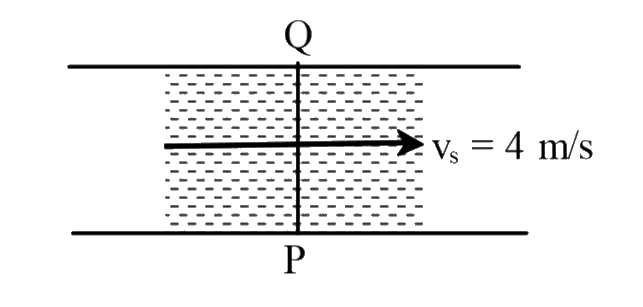
View SolutionA boat man could row his boat with a speed 10 m/sec. He wants to take his boat from P to a point Q just opposite on the other bank of the river flowing at a speed 4 m/sec. He should row his boat–
View SolutionA body moves a distance of 5 m along a straight line under the action of a force 10 N. If the work done is 25√3 joule, the angle which the force makes with the direction of motion of the body is
View SolutionA ball moving with a speed of 9ms−1 strikes an identical stationary ball such that after the collision the direction of each ball makes an angle of 30∘ with the original line of motion. The speeds of two balls after the collision is
View Solution
