The ratio of the area of a regular polygon of n sides inscribed in a circle to that of the polygon of same number of sides circumscribing the same is 3:4. Then the value of n is 6 (b) 4 (c) 8 (d) 12
1
8
12
6
The correct Answer is:D
Step by step video & image solution for The ratio of the area of a regular polygon of n sides inscribed in a circle to that of the polygon of same number of sides circumscribing the same is 3:4. Then the value of n is 6 (b) 4 (c) 8 (d) 12 by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- Solutions of Triangle & Binomial TheoremBOOK - ALLENCHAPTER - Solutions of Triangle & Binomial TheoremEXERCISE - EXERCISE-II
11 Videos
- Solutions of Triangle & Binomial TheoremBOOK - ALLENCHAPTER - Solutions of Triangle & Binomial TheoremEXERCISE - EXERCISE (O-1)
11 Videos
- Solutions of Triangle & Binomial TheoremBOOK - ALLENCHAPTER - Solutions of Triangle & Binomial TheoremEXERCISE - Illustration
28 Videos
- SOLUTION AND PROPERTIES OF TRIANGLEBOOK - ALLENCHAPTER - SOLUTION AND PROPERTIES OF TRIANGLEEXERCISE - All Questions
106 Videos
- TRIGNOMETRIC RATIOS AND IDENTITIESBOOK - ALLENCHAPTER - TRIGNOMETRIC RATIOS AND IDENTITIESEXERCISE - All Questions
1 Videos
Similar Questions
Given that the area of a polygon of n sides circumscribed about a circle is to the area of the circumscribed polygon of 2n sides as 3:2 find n.
View SolutionProve that the area of a regular polygon hawing 2n sides, inscribed in a circle, is the geometric mean of the areas of the inscribed and circumscribed polygons of n sides.
View SolutionIf r is the radius of inscribed circle of a regular polygon of n-sides ,then r is equal to
View SolutionIf a regular polygon of n sides has circum radius R and inradius r then each side of polygon is:
View SolutionThe number of triangles that can be formed form a regular polygon of 2n + 1 sides such that the centre of the polygon lies inside the triangle is
View SolutionFind the radius of the circumscribing circle of a regular polygon of n sides each of length is a.
View SolutionIn the following figure a wire bent in the form of a regular polygon of n sides is inscribed in a circle of radius a. Net magnetic field at centre will be
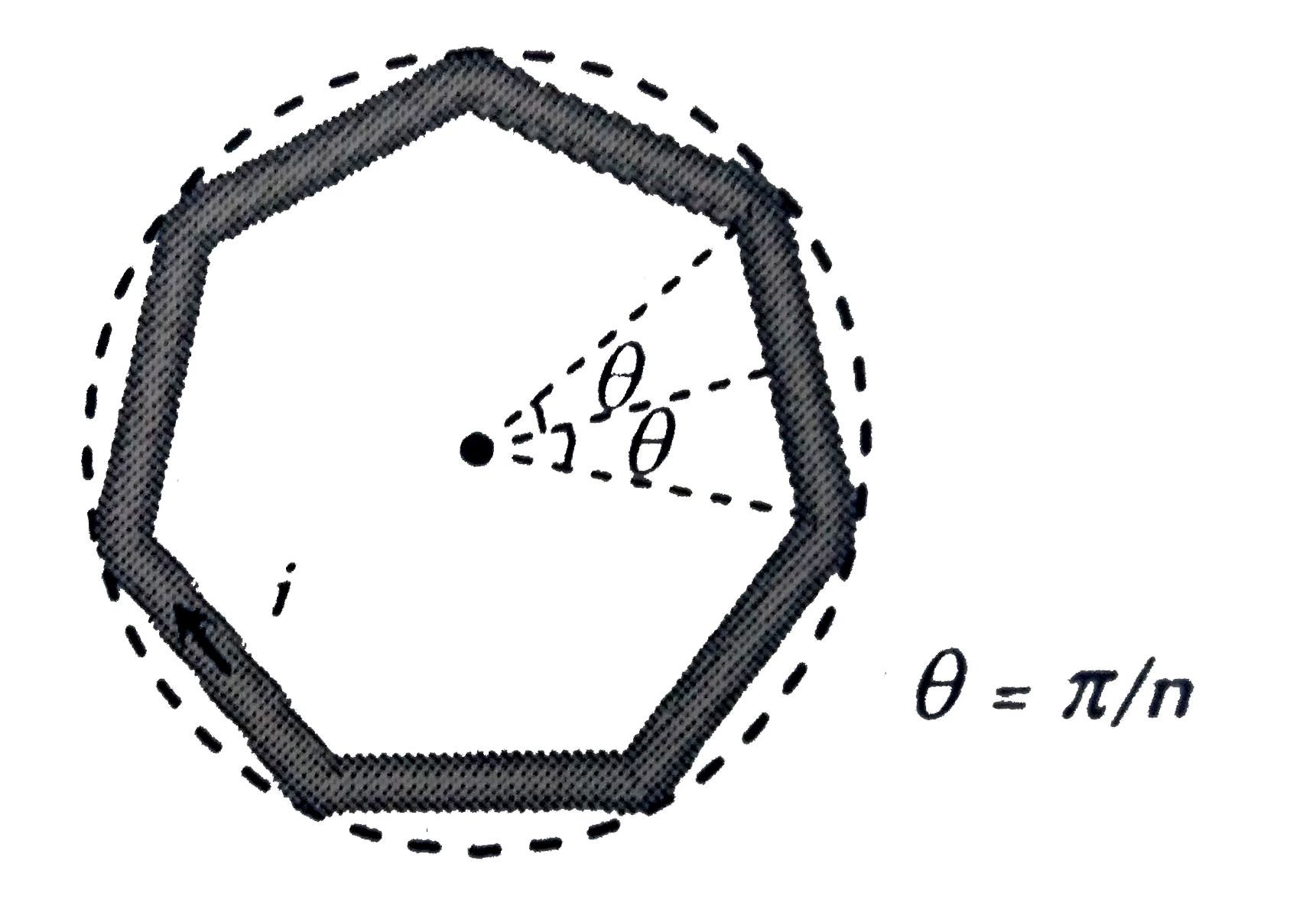
View SolutionIf R is the radius of circumscribing circle of a regular polygon of n-sides,then R =
View SolutionFind the numbers of diagonals in the polygon of n sides.
View SolutionLet An be the area that is outside a n-sided regular polygon and inside its circumscribeing circle. Also Bn is the area inside the polygon and outside the circle inscribed in the polygon. Let R be the radius of the circle circumscribing n-sided polygon. On the basis of above information, answer the equation If n=6 then An is equal to R2(π−√32) (b) R2(2π−6√32) R2(π−√3) (d) R2(2π−3√32)
View Solution
