Assertion : The unit vectors have of distance and dimensions .
Reason : The product of a scalar and a vector of a new scalar.
If both Assertion & Reason are True & Reason is a correct explanation of the Assertion.
If both Assertion & Reason are True but Reason is not a correct explanation of the Assertion.
If Assertion is True but the Reason is False.
If both Assertion & Reason are false.
To solve the question, we need to analyze both the assertion and the reason provided.
Step 1: Analyze the Assertion
The assertion states that the unit vectors ^i,^j,^k have dimensions of distance given as (M0L1T0).
- Unit Vectors: The unit vectors ^i,^j,^k are used to represent directions in a three-dimensional space. They are dimensionless quantities that indicate direction along the x-axis, y-axis, and z-axis, respectively.
- Dimensions of Distance: The dimension of distance is indeed represented as (M0L1T0), where M is mass, L is length, and T is time. Here, M0 indicates that mass does not affect the dimension of distance, L1 indicates that distance is measured in terms of length, and T0 indicates that time does not affect the dimension of distance.
Thus, the assertion is true.
Step 2: Analyze the Reason
The reason states that the product of a scalar and a vector results in a new scalar.
- Scalar and Vector Multiplication: When a scalar quantity is multiplied by a vector quantity, the result is still a vector quantity, not a scalar. For example, if you multiply a scalar (like mass) by a vector (like velocity), the result is a vector quantity (momentum).
- Therefore, the statement that the product of a scalar and a vector is a new scalar is false.
Conclusion
- The assertion is true.
- The reason is false.
Thus, the correct answer is that the assertion is true, but the reason is false.
Final Answer
Assertion is true, Reason is false.
---
The assertion states that the unit vectors ^i,^j,^k have dimensions of distance given as (M0L1T0).
- Dimensions of Distance: The dimension of distance is indeed represented as (M0L1T0), where M is mass, L is length, and T is time. Here, M0 indicates that mass does not affect the dimension of distance, L1 indicates that distance is measured in terms of length, and T0 indicates that time does not affect the dimension of distance.
The reason states that the product of a scalar and a vector results in a new scalar.
- Therefore, the statement that the product of a scalar and a vector is a new scalar is false.
- The assertion is true.
- The reason is false.
Assertion is true, Reason is false.
Topper's Solved these Questions
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT BOOK - ALLENCHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-III
20 Videos
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Question
1 Videos
- SEMICONDUCTORSBOOK - ALLENCHAPTER - SEMICONDUCTORSEXERCISE - Part-3(Exercise-4)
51 Videos
Similar Questions
Find the unit vector of 4ˆi−3ˆj+ˆk.
View SolutionA unit vector perpendicular to both ˆi+ˆjandˆj+ˆk is
View SolutionAssertion : A vector can have zero magnitude if one of its rectangular components is not zero.
Reason : Scalar product of two vectors cannot be a negative quantity.
View SolutionAssertion: The dot product of one vector with another vector may be scalar or a vector.
Reason: If the product of two vectors is a vector quantity, then product is called a dot product.
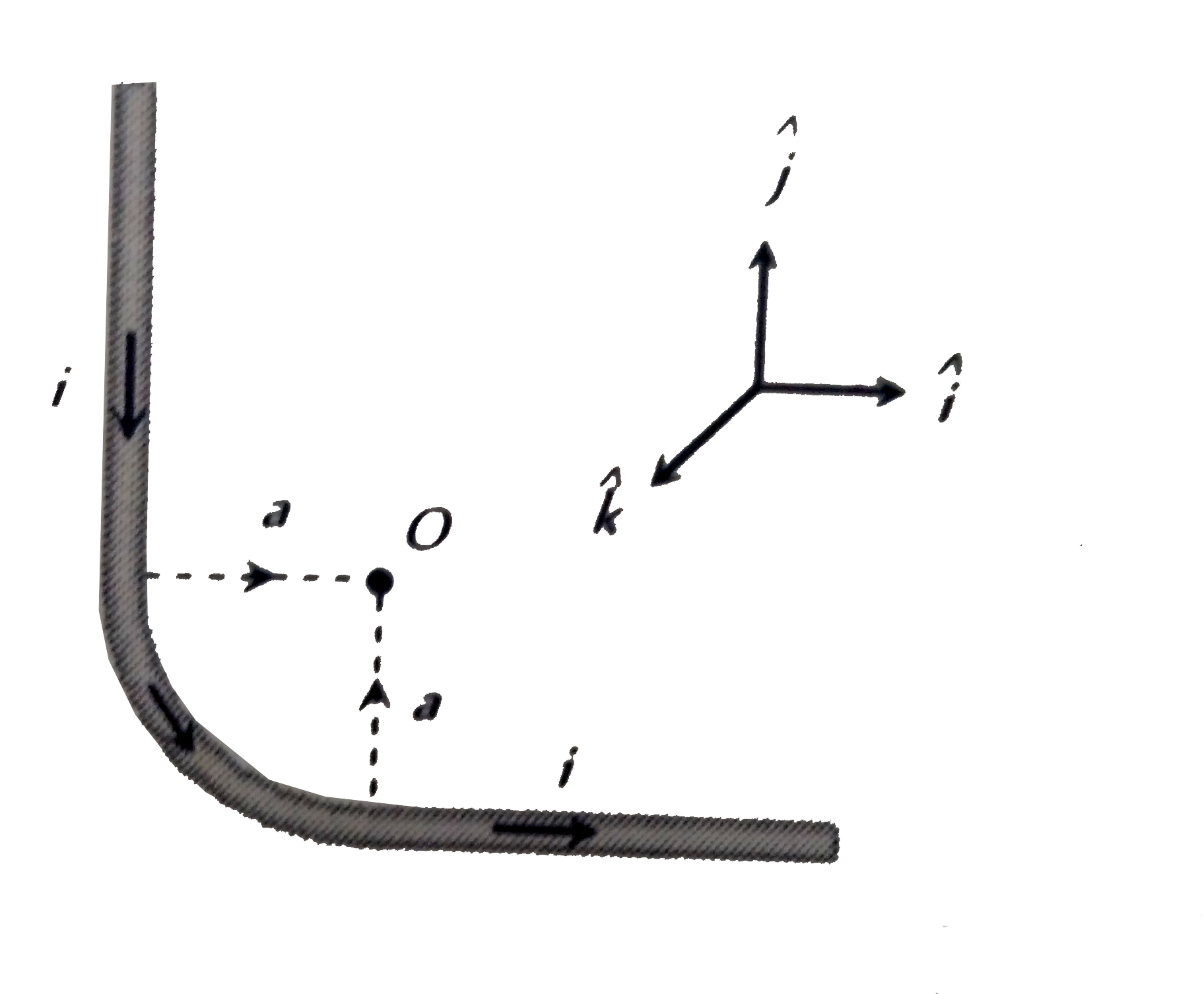
View SolutionThe unit vectors ˆi,ˆj and ˆk are as shown below. What will be the magnetic field at O in the following figure
View SolutionThe scalar product of two vectors A=2ˆi+2ˆj−ˆkandB=−ˆj+ˆk ,is given by
View SolutionFind the resultant of vectors →a=ˆi−ˆj+2ˆkand→b=ˆi+2ˆj−4ˆk. Find the unit vector in the direction of the resultant vector.
View SolutionAssertion: Adding a scalar to a vector of the same dimensions is a meanigful algeraic operation.
Reason: The displacement can be added with distance.
View SolutionConsider the two vectors : →L=1ˆi+2ˆj+3ˆk and →l=4ˆi+ˆj+6ˆk. Find the value of the scalar α such that the vector →L−α→l is perpendicular to →L.
View SolutionAssertion: An object can have constant speed but variable velocity.
Reason: Speed is a scalar but velocity is a vector quantity.
View Solution
