Relation between displacement x and time t is x=2−5t+6t2, the initial acceleration will be :-
−3ms−2
12ms−2
2ms−2
−5ms−2
The correct Answer is:B
To find the initial acceleration from the given displacement-time relation x=2−5t+6t2, we will follow these steps:
Step 1: Differentiate the displacement equation to find velocity
The first step is to differentiate the displacement x with respect to time t to find the velocity v.
v=dxdt=ddt(2−5t+6t2)
Step 2: Calculate the derivative
Now we calculate the derivative term by term:
- The derivative of 2 is 0.
- The derivative of −5t is −5.
- The derivative of 6t2 is 12t.
Putting it all together, we have:
v=0−5+12t=12t−5
Step 3: Differentiate the velocity equation to find acceleration
Next, we differentiate the velocity v with respect to time t to find the acceleration a.
a=dvdt=ddt(12t−5)
Step 4: Calculate the derivative of velocity
Now we calculate the derivative:
- The derivative of 12t is 12.
- The derivative of −5 is 0.
Thus, we find:
a=12
Step 5: Identify the initial acceleration
Since the acceleration a is constant and does not depend on time, the initial acceleration is also 12m/s2.
Final Answer
The initial acceleration is:
12m/s2
---
The first step is to differentiate the displacement x with respect to time t to find the velocity v.
Now we calculate the derivative term by term:
- The derivative of 2 is 0.
- The derivative of −5t is −5.
- The derivative of 6t2 is 12t.
Next, we differentiate the velocity v with respect to time t to find the acceleration a.
Now we calculate the derivative:
- The derivative of 12t is 12.
- The derivative of −5 is 0.
Since the acceleration a is constant and does not depend on time, the initial acceleration is also 12m/s2.
The initial acceleration is:
Topper's Solved these Questions
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (Integration)
Explore 12 Videos
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (Graphs))
Explore 29 Videos
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (Trigonometry)
Explore 22 Videos
- NEWTONS LAWS OF MOTIONBook:ALLENChapter:NEWTONS LAWS OF MOTIONExercise:EXERCISE-III
Explore 28 Videos
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:Example
Explore 1 Video
Similar Questions
If x denotes displacement in time t and x=a cost, then acceleration is :-
View SolutionA particle executes simple harmonic motion with an amplitude of 10 cm and time period 6s. At t=0 it is at position x=5 cm going towards positive x-direction. Write the equation for the displacement x at time t. Find the magnitude of the acceleration of the particle at t=4s.
View SolutionA particle moves along a straight line such that its displacement at any time t is given by s=3t3+7t2+14t+5. The acceleration of the particle at t=1s is
View SolutionA particle is moving in a straight line. Its displacement at time t is given by s(Inm)=4t2+2t, then its velocity and acceleration at time t=12 second are
View SolutionA point mives in a straight line so its displacement x mertre at time t second is given by x2=1+t2. Its aceleration in ms−2 at time t second is .
View SolutionA particle moves along the x-axis in such a way that its x-co-ordinate varies with time as x=2–5t+6t2.
The initial velocity and acceleration of particle will respectively be-
View SolutionA particle moves along a staight line such that its displacement at any time t is given by s=t3−6t2+3t+4m. Find the velocity when the acceleration is 0.
View SolutionDisplacement x versus t2 graph is shown for a particle. The acceleration of particle is
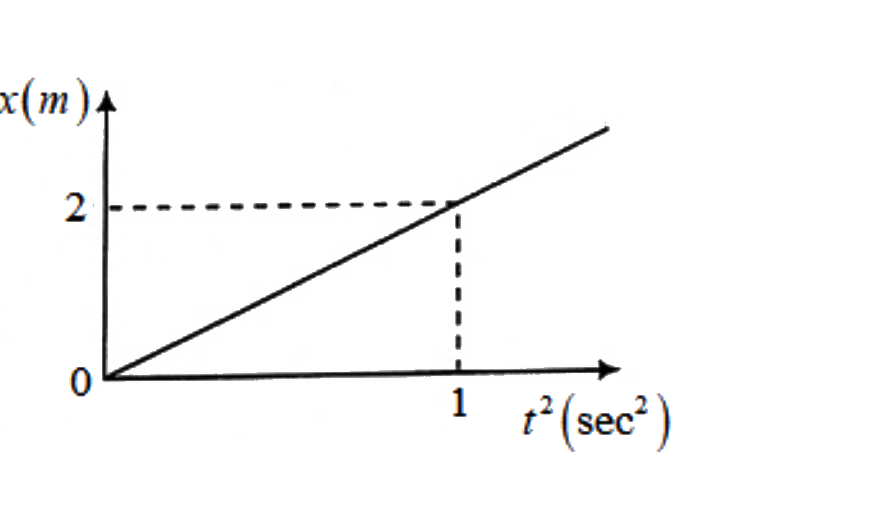
View SolutionFor a particle moving along a straight line, the displacement x depends on time t as x=αt3+βt2+γt+δ. The ratio of its initial acceleration to its initial velocity depends
View SolutionThe relation between time t and distance x is t=ax2+bx where aandb are constants. The acceleration is
View Solution
