If m and n are the two natural number such that mn=25, then find the value of nm:-
The correct Answer is:4
To solve the problem, we need to find the values of m and n given that mn=25, and then calculate nm.
1. Understanding the Equation:
We start with the equation mn=25. We know that 25 can be expressed as 52. This gives us a clue about possible values for m and n.
2. Identifying Possible Values:
Since m and n are natural numbers, we can consider the following pairs:
- If m=5, then n must be 2 because 52=25.
- If m=25, then n must be 1 because 251=25.
Thus, the pairs (m,n) can be (5,2) or (25,1).
3. Calculating nm:
- For the pair (m,n)=(5,2):
nm=25=32
- For the pair (m,n)=(25,1):
nm=125=1
4. Final Result:
The values of nm can either be 32 or 1. Since the problem does not specify which pair to use, both answers are valid. However, the more common interpretation in such problems is to use the pair (5,2).
Thus, the final answer is:
nm=32
We start with the equation mn=25. We know that 25 can be expressed as 52. This gives us a clue about possible values for m and n.
Since m and n are natural numbers, we can consider the following pairs:
- If m=5, then n must be 2 because 52=25.
- If m=25, then n must be 1 because 251=25.
- For the pair (m,n)=(5,2):
nm=25=32
- For the pair (m,n)=(25,1):
nm=125=1
The values of nm can either be 32 or 1. Since the problem does not specify which pair to use, both answers are valid. However, the more common interpretation in such problems is to use the pair (5,2).
nm=32
Topper's Solved these Questions
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (VECTORS)
60 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Units, Dimensions & Measurements)
30 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Graphs))
29 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Video
Similar Questions
Knowledge Check
Two finite sets have m and n elements respectively . The total number of subsets of first set is 56 more than the total number of subsets of the second. Find the values of m and n.
A7,6B6,3C5,1D8,7If m−nn=49, what is the value of nm?
A913B74C95D137
If x is nearly equal to 1 then find the value of mxm−nxnm−n
View SolutionIf variance of first n natural number is 10 and variance of first m even natural number is 16 then the value of m+n is
View SolutionThe value of (m+n)2+(m−n)2 is:
View SolutionProve that there exist no natural numbers, m and n such that m2=n2+2002.
View Solution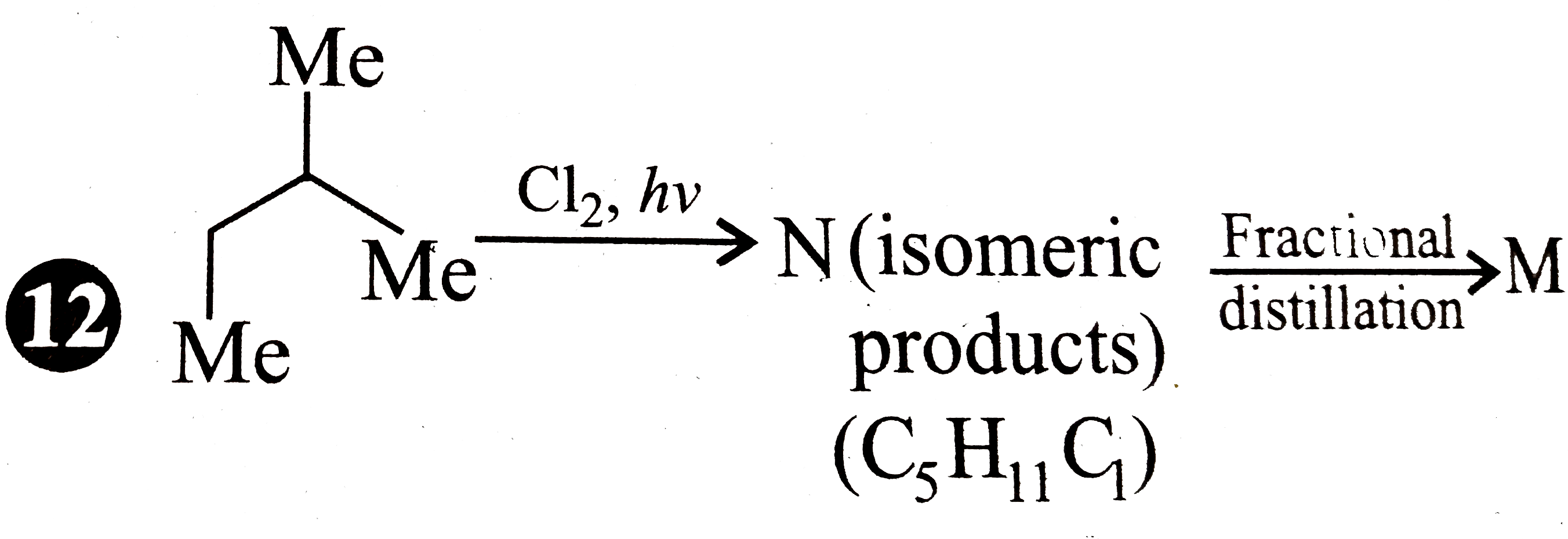
The value of N and M are:
View SolutionIf the G.M. of a and b is an+bnan−1+bn−1 then find the value of n.
View Solution