If →A×→B=→C then find out the correct one :-
→A.→B=0
→A.→C≠0
→B.→C≠0
(→A+→B).→C=0
The correct Answer is:D
To solve the problem, we need to analyze the given information about the vectors A, B, and C, where →A×→B=→C.
1. Understanding the Cross Product:
The cross product →A×→B results in a vector →C that is perpendicular to both →A and →B. Therefore, we can conclude:
→C⊥→Aand→C⊥→B
2. Dot Product of Perpendicular Vectors:
The dot product of two perpendicular vectors is zero. Hence, we can write:
→A⋅→C=0and→B⋅→C=0
3. Analyzing the Options:
- Option A: →A⋅→B=0
- This option states that →A and →B are perpendicular. However, we cannot conclude this from the information given. The only thing we know is that →C is perpendicular to both →A and →B. Therefore, this option is incorrect.
- Option B: →C⋅→A=0
- This option is true since we established that →C is perpendicular to →A.
- Option C: →C⋅→B=0
- This option is also true since →C is perpendicular to →B.
- Option D: →A+→B⋅→C=0
- This can be rewritten as →A⋅→C+→B⋅→C=0. Since both →A⋅→C=0 and →B⋅→C=0, their sum is also zero. Thus, this option is correct.
4. Conclusion:
- The correct options based on the analysis are →C⋅→A=0, →C⋅→B=0, and →A+→B⋅→C=0.
- Therefore, the correct answer is Option D.
The cross product →A×→B results in a vector →C that is perpendicular to both →A and →B. Therefore, we can conclude:
→C⊥→Aand→C⊥→B
The dot product of two perpendicular vectors is zero. Hence, we can write:
→A⋅→C=0and→B⋅→C=0
- Option A: →A⋅→B=0
- This option states that →A and →B are perpendicular. However, we cannot conclude this from the information given. The only thing we know is that →C is perpendicular to both →A and →B. Therefore, this option is incorrect.
- Option B: →C⋅→A=0
- This option is true since we established that →C is perpendicular to →A.
- Option C: →C⋅→B=0
- This option is also true since →C is perpendicular to →B.
- Option D: →A+→B⋅→C=0
- This can be rewritten as →A⋅→C+→B⋅→C=0. Since both →A⋅→C=0 and →B⋅→C=0, their sum is also zero. Thus, this option is correct.
- The correct options based on the analysis are →C⋅→A=0, →C⋅→B=0, and →A+→B⋅→C=0.
- Therefore, the correct answer is Option D.
Topper's Solved these Questions
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Units, Dimensions & Measurements)
30 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (KINEMATICS)
59 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Co-ordinate & Algebra)
37 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
Similar Questions
Find out the correct sentence
View SolutionFind out the correct match
View SolutionFind out the correct match
View SolutionIf →A×→B=→C, then choose the incorrect option : [→Aand→B are non zero vectors]
View SolutionAssertion : If →A,→B,→C are any three non coplanar vectors then →A.(→B×→C)(→C×→A).→B+→B.(→A×→c)→C.(→A×→B)=0, Reason: [→a→b→c]≠[→b→c→a] (A) Both A and R are true and R is the correct explanation of A (B) Both A and R are true R is not te correct explanation of A (C) A is true but R is false. (D) A is false but R is true.
View SolutionIf vector →x satisfying →x×→a+(→x.→b)→c=→d is given by →x=λ→a+→a×→a×(→d×→c)(→a.→c)|→a|2, then find out the value of λ
View SolutionFind out the correct match from the following table and select the option with all the correct one.
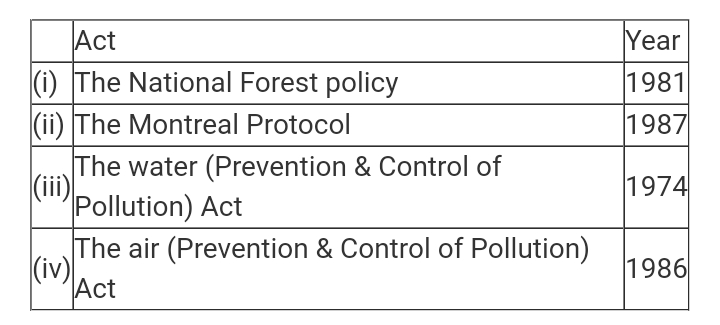
View SolutionIf →A,→B,→C are non-coplanar vectors then →A.→B×→C→C×→A.→B+→B.→A×→C→C.→A×→B=
View SolutionIf →a×→b=→b×→c≠→0, then prove that →a+→c=t→b, where t is a scalar.
View SolutionIf →A×→B=→0 and →B×→C=→0, then the angle between →A and →C may be:
View Solution
