The resistance of each side of an equilateral triangle is 6 ohm. Calculate the equivalent resistance between ends of a side.
6Ω
12Ω
4Ω
8Ω
To find the equivalent resistance between the ends of a side of an equilateral triangle where each side has a resistance of 6 ohms, we can follow these steps:
1. Understand the Configuration:
We have an equilateral triangle with vertices A, B, and C. Each side of the triangle (AB, BC, and CA) has a resistance of 6 ohms.
2. Identify the Resistors:
Let's denote the resistances as follows:
- R1 (AB) = 6 ohms
- R2 (BC) = 6 ohms
- R3 (CA) = 6 ohms
3. Determine the Path for Equivalent Resistance:
To find the equivalent resistance between points A and B, we notice that the resistors R2 (BC) and R3 (CA) are in parallel with each other, while R1 (AB) is in series with the combination of R2 and R3.
4. Calculate the Equivalent Resistance of R2 and R3 in Parallel:
The formula for the equivalent resistance Req of two resistors in parallel R2 and R3 is given by:
1Req=1R2+1R3
Substituting the values:
1Req=16+16=26=13
Therefore,
Req=3 ohms
5. Add the Series Resistance R1:
Now, we add the resistance R1 (which is in series with the parallel combination):
Rtotal=R1+Req=6+3=9 ohms
6. Final Answer:
The equivalent resistance between the ends of a side (A and B) is 9 ohms.
We have an equilateral triangle with vertices A, B, and C. Each side of the triangle (AB, BC, and CA) has a resistance of 6 ohms.
Let's denote the resistances as follows:
- R1 (AB) = 6 ohms
- R2 (BC) = 6 ohms
- R3 (CA) = 6 ohms
To find the equivalent resistance between points A and B, we notice that the resistors R2 (BC) and R3 (CA) are in parallel with each other, while R1 (AB) is in series with the combination of R2 and R3.
The formula for the equivalent resistance Req of two resistors in parallel R2 and R3 is given by:
1Req=1R2+1R3
Substituting the values:
1Req=16+16=26=13
Therefore,
Req=3 ohms
Now, we add the resistance R1 (which is in series with the parallel combination):
Rtotal=R1+Req=6+3=9 ohms
The equivalent resistance between the ends of a side (A and B) is 9 ohms.
Topper's Solved these Questions
Similar Questions
Knowledge Check
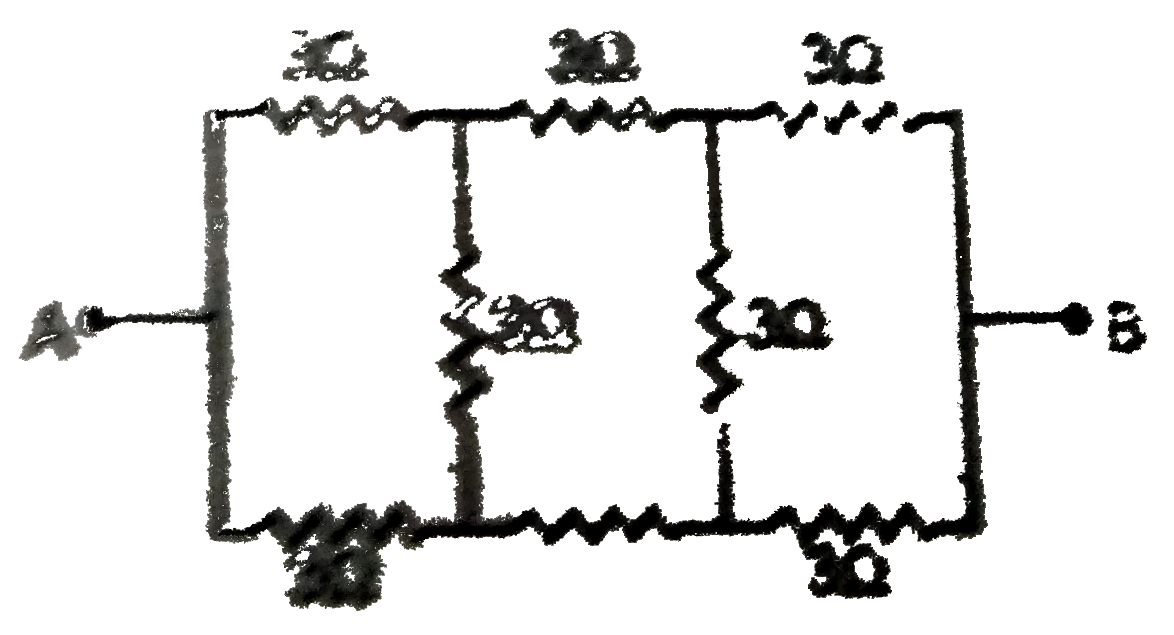
Calculate the equivalent resistance between A and B from the following diagram :
 A5B3C8D4
A5B3C8D4If the side of an equilateral triangle is 6 cm, then its perimeter is
A12 cmB18 cmC27 cmD36 cm
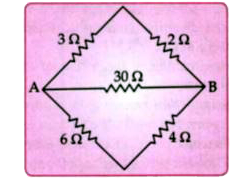
Calculate the equivalent resistance between the points A and B in Fig.
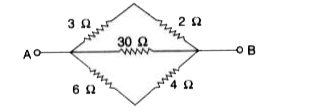
View SolutionEquivalent resistance between A and B is

View SolutionCalculate the equivalent resistance between P and Q from the following diagram:
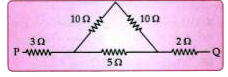
View SolutionCalculate the equivalent resistance between P and Q from the following diagram

View SolutionIn the network shown, each resistance is R. Calculate the equivalent resistance between A and B.
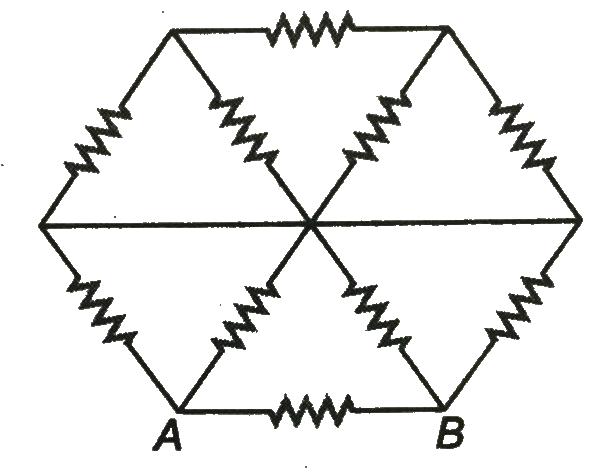
View SolutionFind the altitude of an equilateral triangle of side 8 cm.
View Solution