
Two identical discs of mass m and of radius R touch each other and move with the same velocity perpendicularly to the line segment which joins their centres of mass, along the surface of a horizontal smooth tabletop. There is a third disc of mass M and of radius R at rest, at a point on thhe perpendicular bisector of of the line segment joining the centres of mass of the two moving discs as shown in the figure. The two moving discs collide elastically with the third one, which is at rest there is no friction between the rims of the discs. What should the ratio of M/m be in order that after the collision the two discs of mass m move perpendicularly to their intial velocity?
3
2
The correct Answer is:A

Conservation of momentum of (M+m)
.(i)
Newton's second law:
.(ii)
For 'm' ....(iii)
from (i)
Similar Questions
The moment of inertia of a uniform semicircular disc of mass M and radius r about a line perpendicular to the plane of the disc through the center is
View SolutionTwo spheres each of mass M and radius R are separated by a distance of r. The gravitational potential at the midpoint of the line joining the centres of the spheres is
View Solution
Knowledge Check
Two spheres each of mass M and radius R are separated by a distance of r. The gravitational potential at the midpoint of the line joining the centres of the spheres is
A−GMrB−2GMrC−GM2rD−4GMrTwo identical spheres each of mass M and Radius R are separated by a distance 10R. The gravitational force on mass m placed at the midpoint of the line joining the centres of the spheres is
AzeroB2GMm25R2CGMm25R2DGMm100R2
The moment of inertia of a uniform semicircularwire of mass M and radius r about a line perpendicular to the plane of the wire through the centre is :
View SolutionThree identical spheres each of radius .R. are placed touching each other so that their centres A, B and C lie on a straight line. The position of their centre of mass from A is
View SolutionGiven a uniform disc of mass M and radius R. A small disc of radius R/2 is cut from this disc in such a way that the distance between the centres of the two discs is R/2. Find the moment of inertia of the remaining disc about a diameter of the original disc perpendicular to the line connecting the centres of the two discs
View SolutionA circular disc of mass '2m' and radius '3r' is resting on a flat frictionless surface. Another circular disc of mass m and radius '2r', moving with a velocity 'u'. hits the first disc as shown in the figure. The collision is elastic.
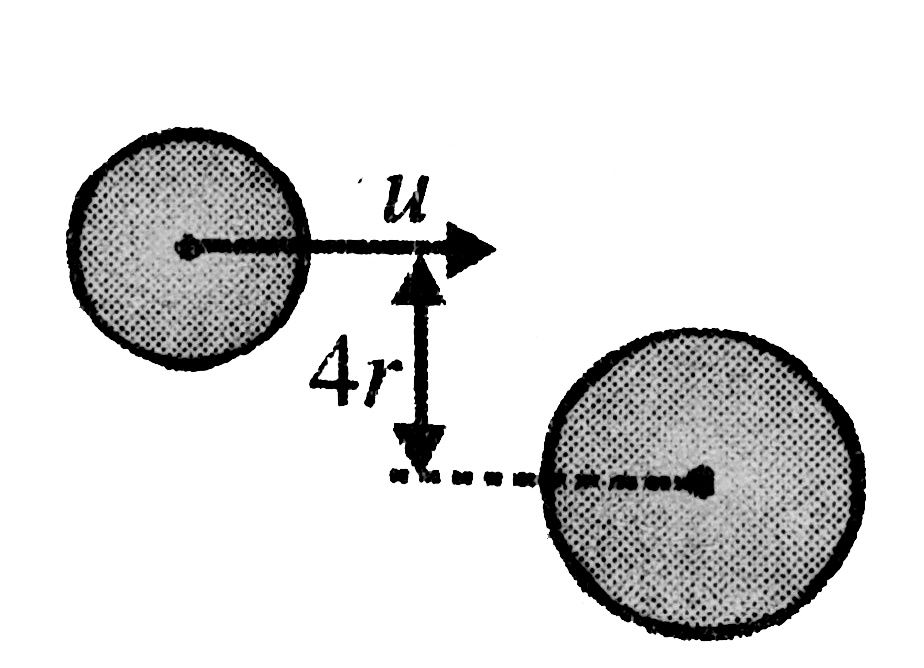 What is the final velocity of the heavier disc?
What is the final velocity of the heavier disc?
View SolutionA disc of radis R is cut out from a larger disc of radius 2R in such a way that the edge of the hole touches the edge of the disc. Locate the centre of mass of the residual disc.
View SolutionA quarter disc of radius R and mass m is rotating about the axis OO' (perpendicular to the plane of the disc) as shown. Rotational kinetic energy of the quarter disc is

View Solution
