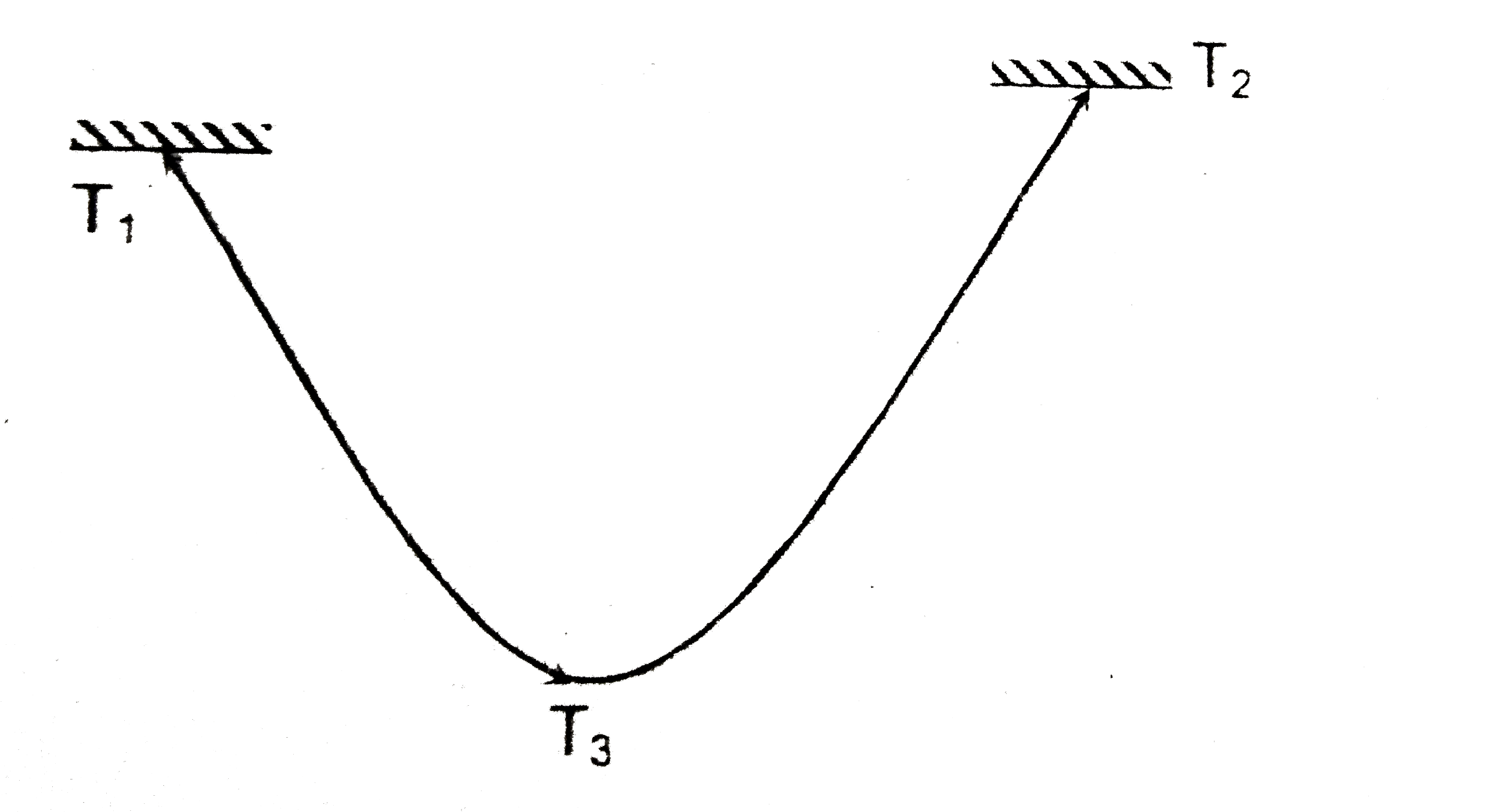
 ltbrltgt A string of mass m (can be non uniform as well) is suspended through two points which are not in same horizontal level. Tension in the string at the end points are T1 and T2 and at the lowest point is T3. Mass of string in terms of T1,T2 and T3 can be represented a (uniform gravity 'g' exists downwards)
ltbrltgt A string of mass m (can be non uniform as well) is suspended through two points which are not in same horizontal level. Tension in the string at the end points are T1 and T2 and at the lowest point is T3. Mass of string in terms of T1,T2 and T3 can be represented a (uniform gravity 'g' exists downwards)
√T21−T23+√T22−T23g
(T1+T2−2T3)g
√T21+T22g
√T21+T23+√T22+T23g
The correct Answer is:A
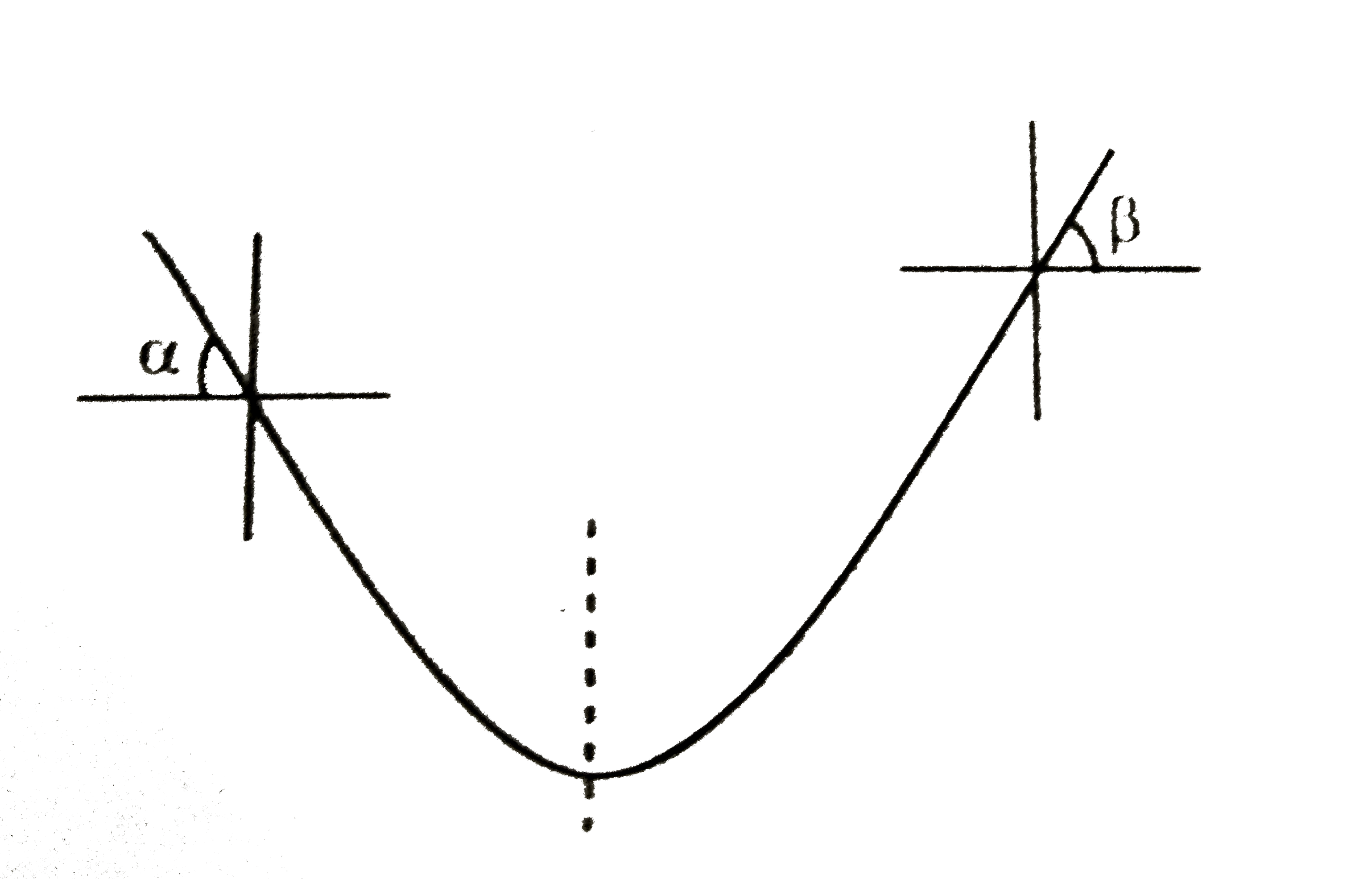
T1cosα=T3=T2cosβ
T1sinα+T2sinβ=mg
⇒mg=T1√1−(T3T1)2+T2√1−(T3T2)2
⇒m=√T21+T23+√T22−T23g
Similar Questions
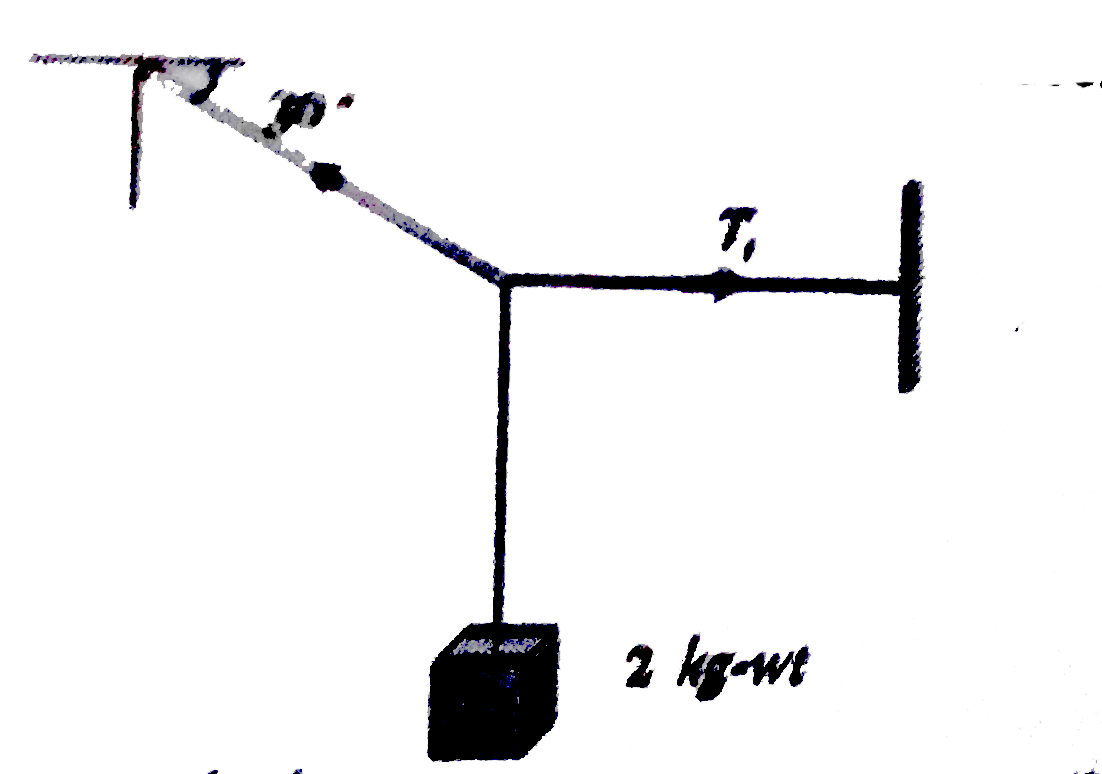
Determine the tensions T1 and T2 in the string as shown in figure.
View SolutionDetermine the tensions T1 and T2 in the string as shown in figure.

View SolutionA particle of mass m is tied to a string of length L and whirled into a horizontal plan. If tension in the string is T then the speed of the particle will be :
View SolutionIf the normals drawn at the points t1 and t2 on the parabola meet the parabola again at its point t3, then t1t2 equals.
View SolutionA cylinder of mass m is suspended through two strings wrapped around it as shwon in figure . Find a. the tension T in the string and b. the speed o the cylinder as it falls through a distance h.

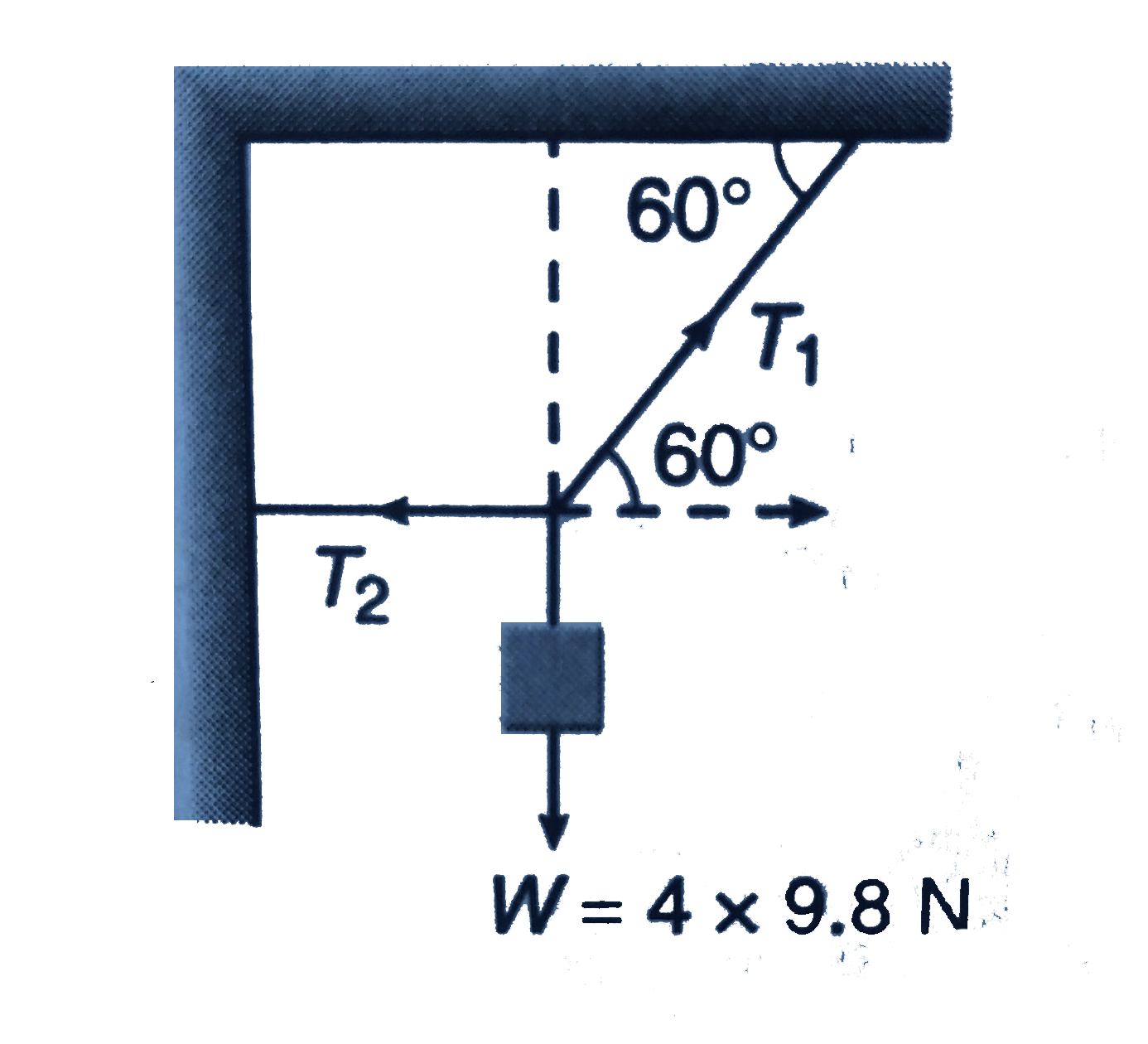
View SolutionA body of weight 2 kg is suspended as shown in the figure. The tensionT1 in the horizontal string (in kg wt ) is
View SolutionIf tension in string A and string B are TA and TB then find out TATB (assume that stringe are light and g=10m/s2) :
View SolutionA body of weight 2 kg is suspended as shown in the figure. The tension T2 in the horizontal string (in kg wt) is :-
View SolutionA uniform rod of mass m and length L is suspended with two massless strings as shown in the figure. If the rod is at rest in a horizontal position the ratio of tension in the two strings T1T2 is:

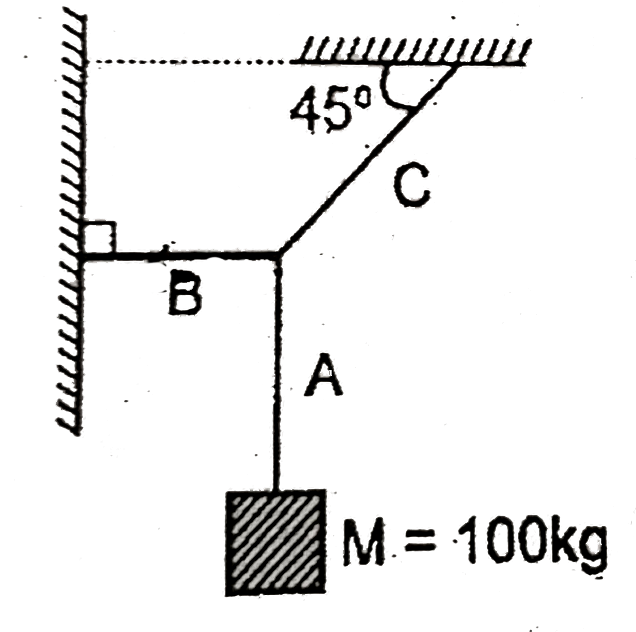
View SolutionA block of weight W is supported by three strings as shown in figure. Which of the following relations is true for tension in the string ? (Here, T1,T2 and T3 are the tension in the strings A,B and C respectively)

View Solution
