
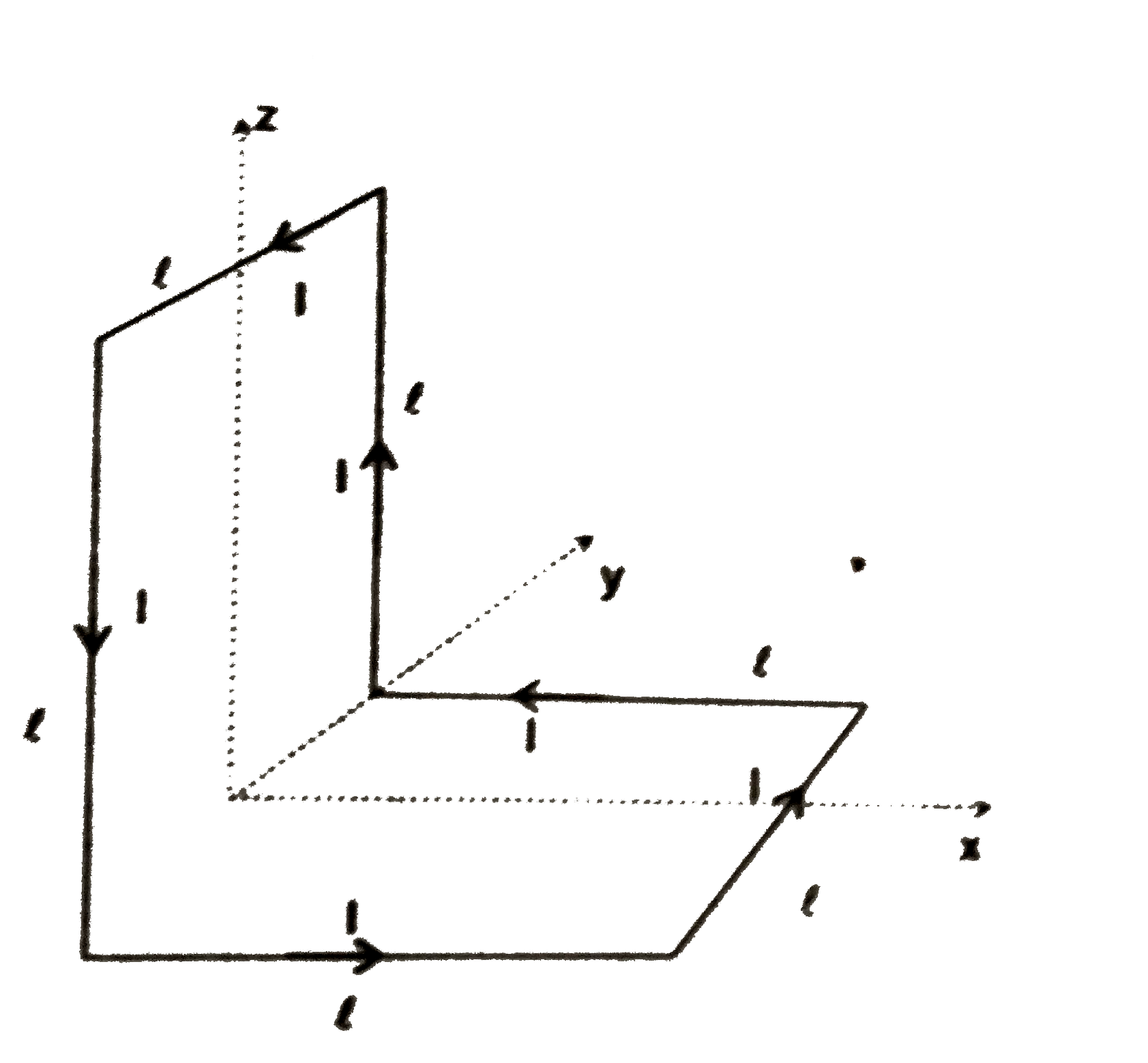
A conducting wire MN carrying a current I is bent into the shape as shown and placed in xy plane. A uniform magnetic field →B=−Bˆk is existing in the region. The net magnetic force experenced by the conducting wire MN is
2BIR
3BIR
4BIR
6BIR
The correct Answer is:D
Since →B is constant in the region The net magnetic force experienced by the conducting by the conducting wire MN is
→F=l(→Leff×→B)
where →Leff=6Rˆi
→F=l[6Rˆi×B(−ˆk)]
F=6BlR(ˆj)
Similar Questions
A conducting loop carrying current 'l' is bent into two halves and placed in mutually perpendicular planes xy and yz planes as shown. A uniform magnetic field →B=Bˆj is existing in the region. The net magnetic torque experienced by the loop is
View Solution
A conducting wire carrying a current I is bent into the shape as shown. The net magnetic field at the centre O of the circular arc of radius R
View SolutionA long wire carrying current 'I' is bent into the shape as shown in the figure. The net magnetic field intensity at the centre 'O' is

View SolutionA wire carrying current i is bent as shown in figure and placed in the plane of uniform magnetic field Bvec. The magnitude of magnetic force experienced by
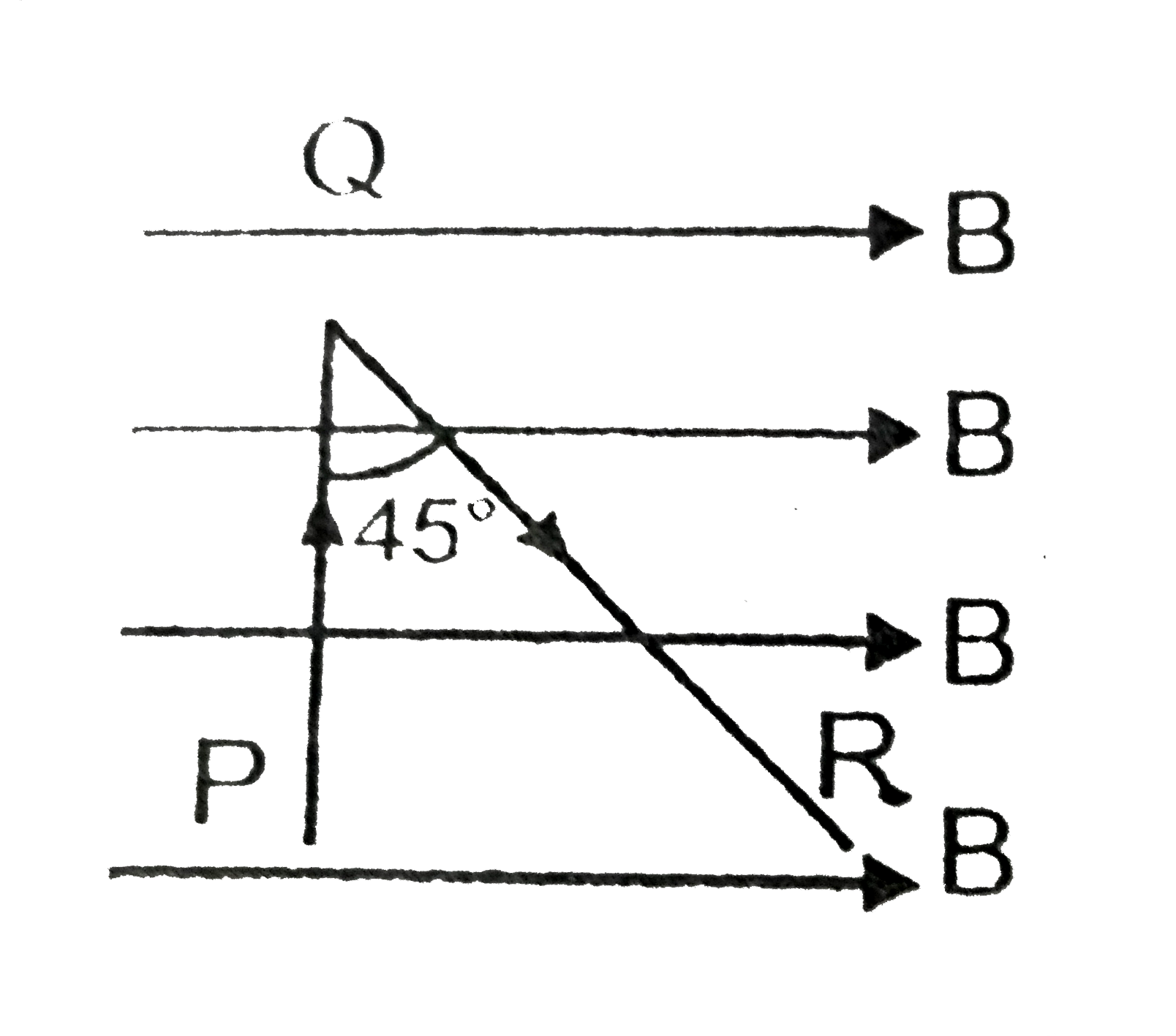
View SolutionA wire PQR carrying a current l is bent as shown in the figure. It is placed in a uniform magnetic field B. What is the ratio of magnitude of the force on PQ to that on QR ?
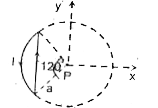
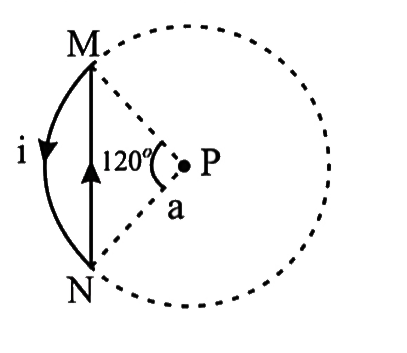
View SolutionA wire loop carrying current I is placed in the x-y plane as shown. Magnetic induction at P is
View SolutionA wire loop carrying current I is placed in the x−y plane as shown in the figure. If an external uniform magnetic field →B=Bˆi is switched on, then the torque acting on the loop is
View SolutionA conducting wire carrying current I is shown in the figure. The magnitude of magnetic field at the point P will be

View SolutionA wire carrying a 10A current is bent to pass through various sides of a cube of side 10 cm as shown in fig. A magnetic field →B=(2ˆi−3ˆj□)T is present in the region.

Find the net force on the loop shown.
View SolutionA part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is

View Solution
