If photoelectrons emitted by a metl on irradiating it by a light of wave length λ cannot move away farther than a distance 'd' in presence of a retarding electric field E, find threshold wavelength of the metal.
λc/eEd
λ+hceEd
λ−hceEd
[1λ−eEdhc]−1
The correct Answer is:D
To solve the problem, we need to find the threshold wavelength (λ0) of the metal based on the given conditions. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the Photoelectric Effect
The photoelectric effect states that when light of a certain wavelength (λ) strikes a metal surface, it can emit electrons. The energy of the incident photons is given by the equation:
E=hcλ
where h is Planck's constant and c is the speed of light.
Step 2: Relate the Energy to the Work Function
The emitted electrons can only escape if the energy of the incoming photons exceeds the work function (ϕ) of the metal. The threshold wavelength (λ0) is the maximum wavelength that can still cause photoemission, given by:
ϕ=hcλ0
Step 3: Apply the Photoelectric Equation
According to Einstein's photoelectric equation:
K.E.=hcλ−ϕ
where K.E. is the kinetic energy of the emitted electrons.
Step 4: Consider the Retarding Electric Field
In the presence of a retarding electric field E, the electrons experience a force that opposes their motion. The maximum kinetic energy of the electrons can be expressed as:
K.E.=12mev2
where me is the mass of the electron and v is its velocity.
Step 5: Relate Velocity to the Electric Field
The acceleration a of the electrons in the electric field E is given by:
a=eEme
Using the kinematic equation v2=u2+2as (where u=0 when the electrons are emitted), we can write:
v2=2ad=2(eEme)d
Thus,
v=√2eEdme
Step 6: Substitute into the Photoelectric Equation
Substituting v back into the photoelectric equation gives:
hcλ−ϕ=12me(√2eEdme)2
This simplifies to:
hcλ−ϕ=eEd
Step 7: Solve for the Threshold Wavelength
Rearranging the equation, we have:
hcλ=ϕ+eEd
Substituting ϕ=hcλ0:
hcλ=hcλ0+eEd
Rearranging gives:
hcλ−eEd=hcλ0
Thus,
1λ0=1λ−eEdhc
Step 8: Final Expression for Threshold Wavelength
Taking the reciprocal gives:
λ0=11λ−eEdhc
Conclusion
Thus, the threshold wavelength of the metal is given by:
λ0=hceEd+hcλ
The photoelectric effect states that when light of a certain wavelength (λ) strikes a metal surface, it can emit electrons. The energy of the incident photons is given by the equation:
E=hcλ
where h is Planck's constant and c is the speed of light.
The emitted electrons can only escape if the energy of the incoming photons exceeds the work function (ϕ) of the metal. The threshold wavelength (λ0) is the maximum wavelength that can still cause photoemission, given by:
ϕ=hcλ0
According to Einstein's photoelectric equation:
K.E.=hcλ−ϕ
where K.E. is the kinetic energy of the emitted electrons.
In the presence of a retarding electric field E, the electrons experience a force that opposes their motion. The maximum kinetic energy of the electrons can be expressed as:
K.E.=12mev2
where me is the mass of the electron and v is its velocity.
The acceleration a of the electrons in the electric field E is given by:
a=eEme
Using the kinematic equation v2=u2+2as (where u=0 when the electrons are emitted), we can write:
v2=2ad=2(eEme)d
Thus,
v=√2eEdme
Substituting v back into the photoelectric equation gives:
hcλ−ϕ=12me(√2eEdme)2
This simplifies to:
hcλ−ϕ=eEd
Rearranging the equation, we have:
hcλ=ϕ+eEd
Substituting ϕ=hcλ0:
hcλ=hcλ0+eEd
Rearranging gives:
hcλ−eEd=hcλ0
Thus,
1λ0=1λ−eEdhc
Taking the reciprocal gives:
λ0=11λ−eEdhc
Thus, the threshold wavelength of the metal is given by:
λ0=hceEd+hcλ
Similar Questions
Stopping potential of emitted photo electron is V when monochromatic light of wavelength 'lamda' incident on a metal surface. If wavelength of light incident becomes 'lambda/3' stopping potential of photoelectrons becomes V/4 then the threshold wavelength of metal is k'lambda' then k will be
View SolutionWhen a certain metal was irradiated with a light of 8.1×1016 Hz frequency the photoelectron emitted had 1.5 times the kinetic energy as did the photoelectrons emitted when the same metal was irradiated with light 5.8×1016 Hz frequency if the same metal is irradiated with light of 3.846 nm wave length what will be the energy of the photoelectron emitted ?
View SolutionA monochromatic light of wavelength λ is incident on an isolated metallic sphere of radius a. The threshold wavelength is λ0 which is larger than λ. Find the number of photoelectrons emitted before the emission of photoelectrons will stop.
View SolutionThe apparent wavelength of light from a star moving away from the earth is 0.02% more than the actual wave length. What is the velocity of star
View SolutionWhen a surface is irradiated with light of wavelength 4950A, a photocurrent appears which vanishes if a retarding potential greater than 0.6V is applied across the photo tube. When a different source of light is used, it is found that the critical retarding potential is changed to 1.1V. Find the work function of the emitting surface and the wavelength of the second source.
View SolutionPhotons emitted by a gas consisting of excited hydrogen like atoms (A) during a transition from a higher quantum state (quantum no. n) to a lower quantum state (quantum no :m ) are incident on a metallic surface (B) causing the emission of photoelectrons . The fastest photoelectrons pass undeviated through a region consisting of electric field E0=3.7 V/cm and magnetic field B0=103T , oriented in perpecdicular directions and the photoelctrons enter the region perpendicular to both the electric and magnetic field
The threshold wavelength for the metal B equal 830 nm. the spectrum of radiations emitted by the excited hydrogen -like atoms (A) consists of 15 different wavelengths .
Find the quantum numbers of the states n,m and atomic number (Z) of the element (A) . (Take 1.89/13.6≈1/7)View SolutionIn a historical experiment to determine Planck's constant, a metal surface was irradiated with light of different wavelengths. The emitted photoelectron energies were measured by applying a stopping potential. The relevant data for the wavelength (λ). ) of incident light and the corresponding stopping potential (V0) are given below :
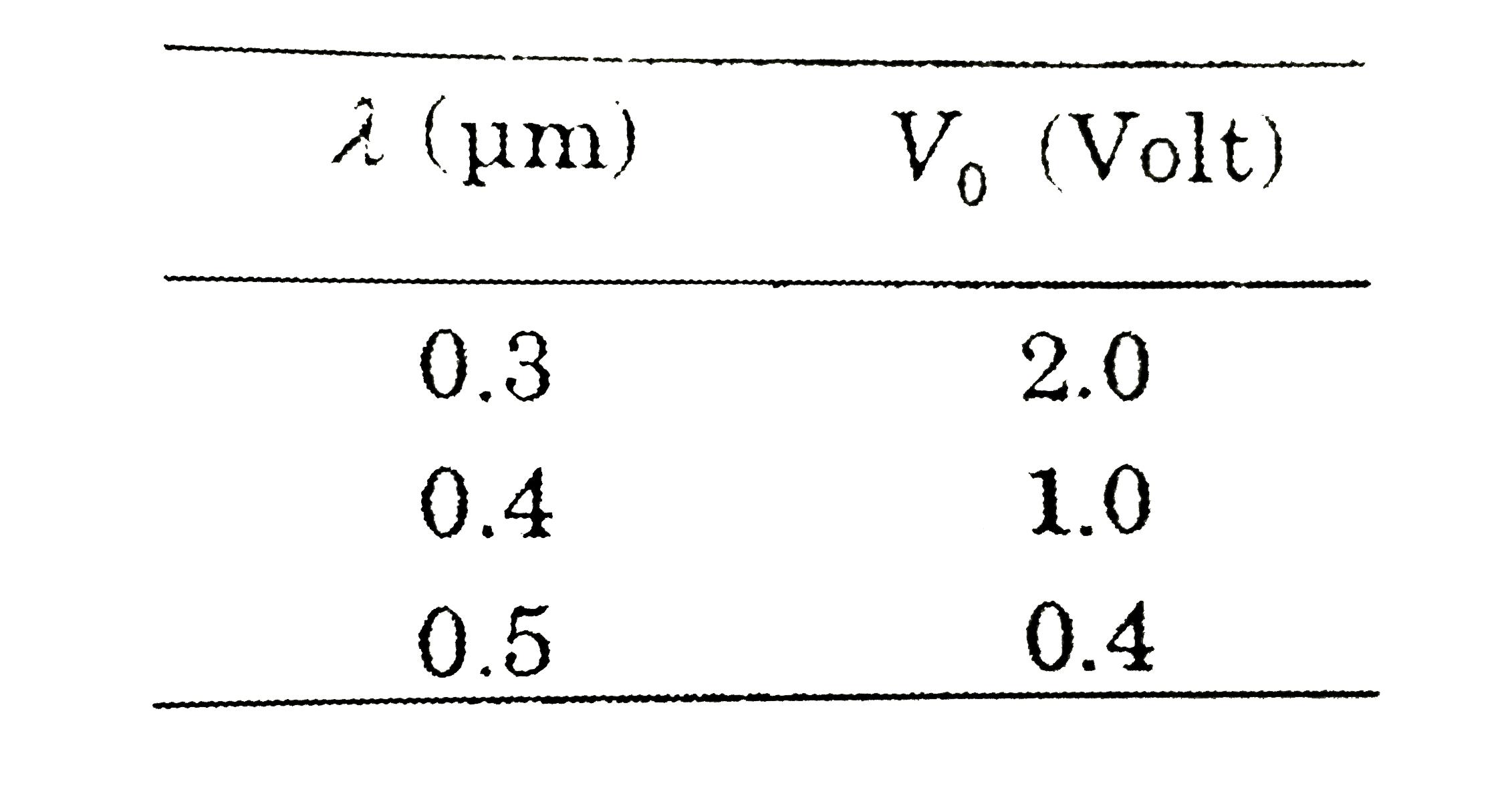
Given that c=3×108ms−1ande=1.6×10−19C Planck's constant (in units of J s) found from such an experiment isView SolutionConsider the situation shown in figure. The two slits S1andS2 placed symmetrically around the central line are illuminated by a monochromatic light of wavelength λ. The separation between the slits is d. The light transmitted by the slits falls on a screen Σ1 placed at a distance D from the slits. The slit S3 is at the placed central line and the slit S4, is at a distance z from S3. Another screenΣ2 is placed a further distance D away from 1,1. Find the ratio of the maximum to minimum intensity observed on Σ2 if z is equal to a. z=λD2d b. λDd c. λD4d
 View Solution
View SolutionThe path of photoelectrons emitted due to electromagnetic radiation incident on a sample of material A, is found to have a maximum bending radius of 0.1 m in a magnetic field of (√23)×10−4T. When the radiation is incident normally on a double slit having a slit separation of 0.1mm, it is observed that there are 10 fringes in a width of 3.1 cm on a screen placed at a distance of 1 m from the double slit. Find the work function of the material. and the corresponding threshold wavelength. What sould be the wavelength of the incident light so that the bending radius is one-half of what it was before? Given that mass of the electron=0.5MeVc2,hc=12400eV−A
View SolutionThe emission of electrons from a metal surface exposed rto light radaition of appropriate wavelength is called photoelectroic effect .The emmited electron are called photo=-weklectron work function of threshold energy may be defined as the minimum amount of energy required to ejercted electron from a most surface .According to Einstein
Maximum kinetic energy of ejected electron = Aborbed energy - Work function
12mv2max=h(v)−h(vn)=hv[1λ−01λn]
Where vn and λ0 are thereshold frequency and threshold wavelength respectively
Sopping potential : it is the miximum potential at which the photoelectric current becomes zero if V0 is the stopping potential eV0=h(v−v0)
The folloeing figure indicates the energy livels of a certain atom .When the system moves from 2E level to E lvel a photon of wavelength λ is emitted .The wavelength of the photon produced during the transition from level 4E/3 to level E is
 View Solution
View Solution

