A hollow circular tube of radius R and negligible internal diameter is fixed on horizontal surface ball A of mas m is given velocity vo in the shown direction. It collides with ball B of mass 2m. Collision is perfectly elastic. If centre of loop is origin of co-ordinates system, then co-ordinate of next collision is
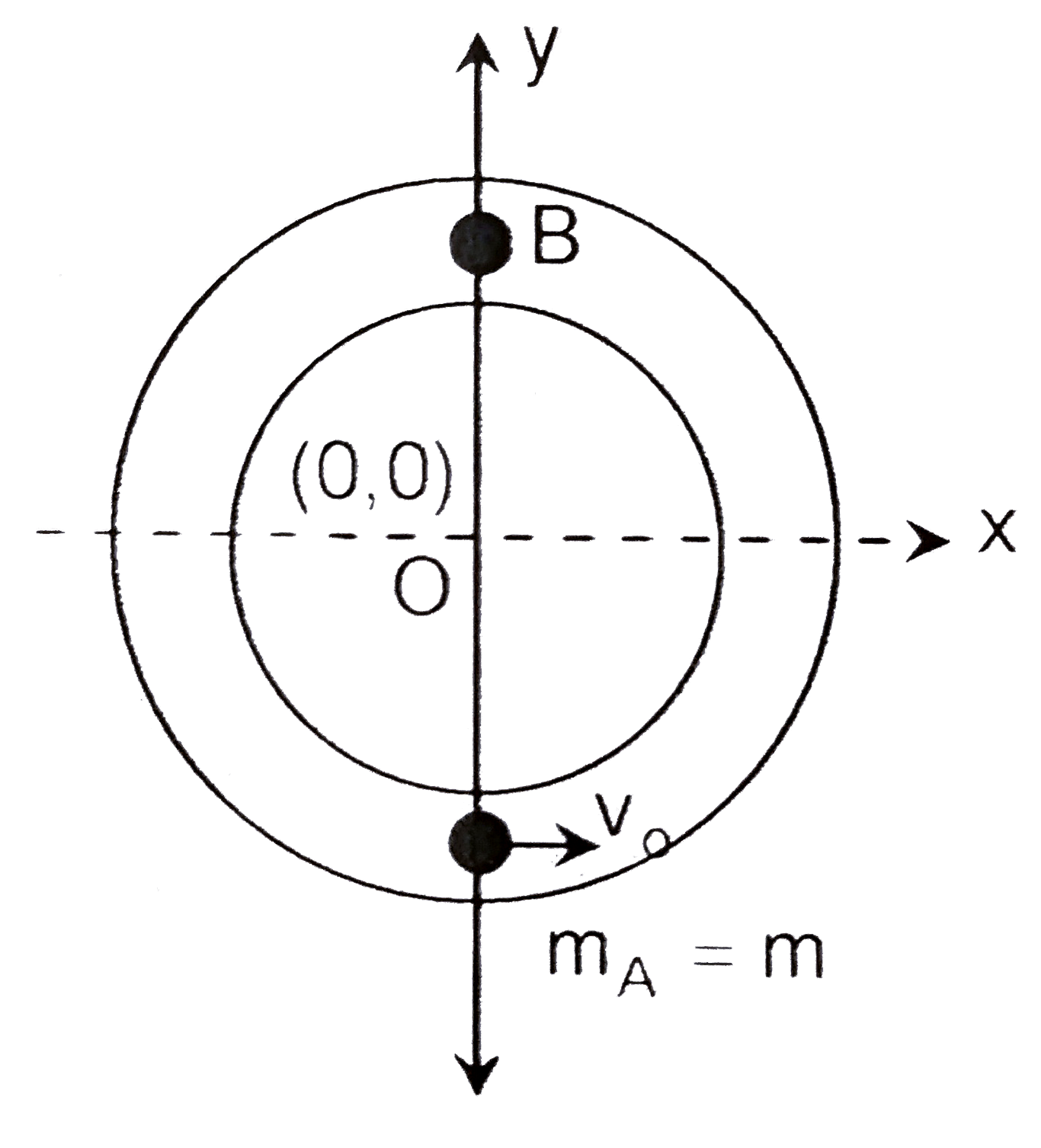
(√32R,−R2)
(−√32R,R2)
(R2,−√32R)
(R2,R2)
The correct Answer is:C
−mvo+o=mv1+2mv2
−vo=v1+2v2….(i) & e=v2−v1−vo=1
∴V2−v1=−vo…. (ii) from (i) & (ii) v1=vo3,v2=−2vo3
∴T=2πRvo
Angle rotated by by A=2π3, Angle rotated by B=4π3rad.
Similar Questions
Two identical balls, each of mass m, are tied with a string and kept on a frictionless surface. Initially, the string is slack. They are given velocities 2u and u. in the same direction. Collision between the balls is perfectly elastic.

What is the impulse generated in the string during the first collision?
View SolutionTwo identical balls, each of mass m, are tied with a string and kept on a frictionless surface. Initially, the string is slack. They are given velocities 2u and u. in the same direction. Collision between the balls is perfectly elastic.

After the first collision, what is the total loss in kinetic energy of the balls?
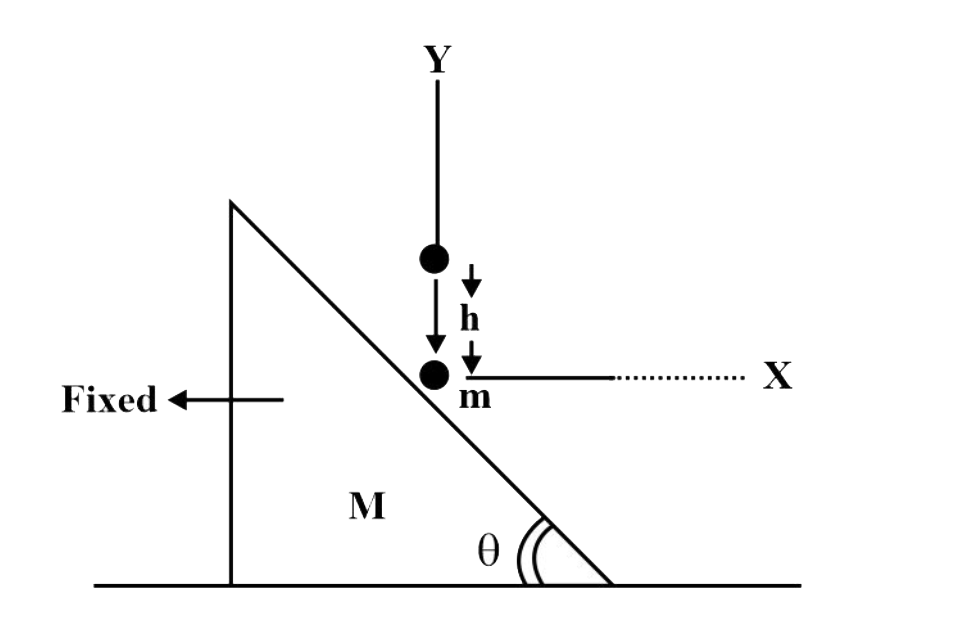
View SolutionA ball of mass m is dropped onto a smooth fixed wedge of inclination θ The collision is perfectly elastic . If after the collision, the x component of the velocity of the block is √2gh , then θ is
View SolutionTwo identical balls, each of mass m, are tied with a string and kept on a frictionless surface. Initially, the string is slack. They are given velocities 2u and u. in the same direction. Collision between the balls is perfectly elastic.

What is the final loss in kinetic energy of the balls?
View SolutionA ball of mass m moving with velocity v collides head on elastically with another identical ball moving with velocity - V. After collision
View SolutionA particle A of mass m and initial velocity v collides with a particle of mass m/2 which is at rest. The collision is head on, and elastic. The ratio of the de-broglie wavelength λAandλB after the collision is
View SolutionA point mass m collides with a disc of mass m and radius R resting on a rough horizontal surface as shown . Its collision is perfectly elastic. Find angular velocity of the disc after pure rolling starts

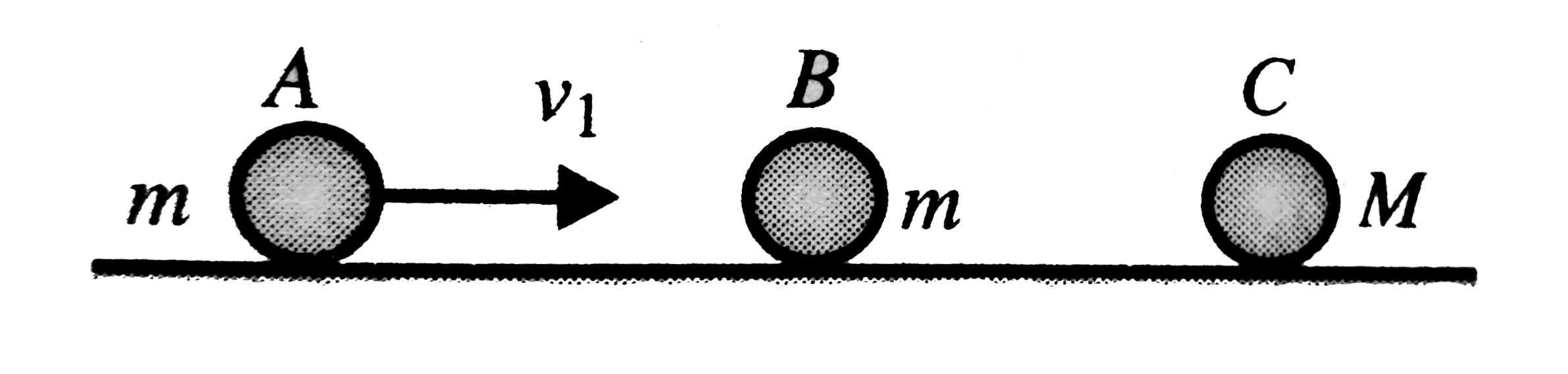
View SolutionTwo balls A and B each of mass m are placed on a smooth ground as shown in the figure. Another ball C of mass M arranged to the right of ball B as shown. If a velocity v1 is given to ball A in rightward direction, consider two cases. Case-I M>m and case-II M<m. Take all the collisions perfectly elastic (e=1), find the number of collision in case-I and case-II.
View SolutionA ball of mass m moving with velocity v collides head-on which the second ball of mass m at rest. I the coefficient of restitution is e and velocity of first ball after collision is v1 and velocity of second ball after collision is v2 then
View SolutionA ball of mass m moving with velocity u collides head-on which the second ball of mass m at rest. If the coefficient of restitution is e and velocity of first ball after collision is v1 and velocity of second ball after collision is v2 then
View Solution
