Capacitors C1=1μF and C2=2μF are separately charged from the same battery. They are allowed to discharge separately through equal resistors
The currents in the two dicharging circuits at t=0 is zero
The currents in the two discharging circuits at t=0 are equal but not zero
The currents in the two discharging circuits at t=0 are unequal
C1 loses 50% of its initial charge sooner than C20 loses 50% of its initial charge.
The correct Answer is:B, D
To solve the problem step by step, we will analyze the discharging process of the capacitors C1 and C2 through equal resistors.
Step 1: Write the equations for discharging current
The current I during the discharging of a capacitor is given by the equation:
I(t)=I0e−t/(RC)
where I0 is the initial current, R is the resistance, C is the capacitance, and t is time.
For capacitor C1:
I1(t)=I10e−t/(RC1)
For capacitor C2:
I2(t)=I20e−t/(RC2)
Step 2: Determine the initial currents
Since both capacitors are charged from the same battery and discharged through the same resistor, the initial currents I10 and I20 are equal:
I10=I20=VR
where V is the voltage of the battery.
Step 3: Analyze the current at t=0
At t=0:
I1(0)=I10andI2(0)=I20
Thus, both currents are equal and non-zero:
I1(0)=I2(0)=VR
Step 4: Determine the time for 50% discharge
The charge Q on a capacitor is given by:
Q(t)=Q0e−t/(RC)
For 50% discharge, we set Q(t)=Q02:
Q02=Q0e−t/(RC)
Dividing both sides by Q0 and rearranging gives:
12=e−t/(RC)
Taking the natural logarithm:
ln(12)=−tRC
Thus,
t=−RCln(12)=RCln(2)
For C1:
t1=RC1ln(2)
For C2:
t2=RC2ln(2)
Step 5: Compare the discharge times
Given that C1=1μF and C2=2μF:
t1=R(1×10−6)ln(2)
t2=R(2×10−6)ln(2)
Since C2>C1, it follows that:
t2>t1
This means C1 discharges 50% of its charge sooner than C2.
Conclusion
- The currents at t=0 are equal but not zero.
- Capacitor C1 loses 50% of its initial charge sooner than capacitor C2.
Final Answers
1. The currents in the two discharging circuits at t=0 are equal but not zero.
2. Capacitor C1 loses 50% of its initial charge sooner than capacitor C2.
The current I during the discharging of a capacitor is given by the equation:
I(t)=I0e−t/(RC)
where I0 is the initial current, R is the resistance, C is the capacitance, and t is time.
I1(t)=I10e−t/(RC1)
For capacitor C2:
I2(t)=I20e−t/(RC2)
Since both capacitors are charged from the same battery and discharged through the same resistor, the initial currents I10 and I20 are equal:
I10=I20=VR
where V is the voltage of the battery.
At t=0:
I1(0)=I10andI2(0)=I20
Thus, both currents are equal and non-zero:
I1(0)=I2(0)=VR
The charge Q on a capacitor is given by:
Q(t)=Q0e−t/(RC)
For 50% discharge, we set Q(t)=Q02:
Q02=Q0e−t/(RC)
Dividing both sides by Q0 and rearranging gives:
12=e−t/(RC)
Taking the natural logarithm:
ln(12)=−tRC
Thus,
t=−RCln(12)=RCln(2)
t1=RC1ln(2)
For C2:
t2=RC2ln(2)
Given that C1=1μF and C2=2μF:
t1=R(1×10−6)ln(2)
t2=R(2×10−6)ln(2)
Since C2>C1, it follows that:
t2>t1
This means C1 discharges 50% of its charge sooner than C2.
- The currents at t=0 are equal but not zero.
- Capacitor C1 loses 50% of its initial charge sooner than capacitor C2.
1. The currents in the two discharging circuits at t=0 are equal but not zero.
2. Capacitor C1 loses 50% of its initial charge sooner than capacitor C2.
Similar Questions
A capacitor C1 of capacitance 1μF and a capacitor C2 of capacitance 2μF are separately charged by a common battery for a long time. The two capacitors are then separately discharged through equal resistors. Both the discharge circuits are connected at t=0.
View SolutionA capacitor C1 of capacitance 1μF and a capacitor C2 of capacitance 2μF are separately charged by a common battery for a long time. The two capacitors are then separately discharged through equal resistors. Both the discharge circuits are connected at t=0.
View SolutionA capacitor of capacitance 100(μ)F is connected across a battery of emf6.0V through a resistance of 20k(Ω)for 4.0s after the battery is disconnecting?
View SolutionTwo capacitors C1andC2(C1>C2) are charged separtately to same potential. Now they are allowed to discharge through similar resistors. Initial rate of discharging will be
View SolutionTwo capacitors C1=4μFandC2=2μF are charged to same potential V = 500 Volt, but with opposite polarity as shown in the figure. The switches S1andS2 are closed.

View SolutionThree capacitors C1=6μF,C2=12μF and C3=20μF are connected to a 100 V battery, as shown in figure below:
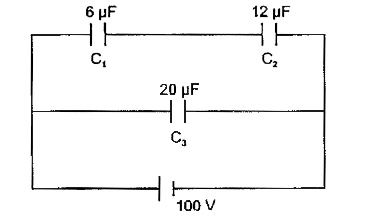
(i) Charge on each plate of capacitor C1.
(ii) Electrostatic potential energy stored in capacitor C3.
View SolutionTwo capacitors of capacitances C1=2μF and C2=8μF are connected in series and the resulting combination is connected across a 300V battery. Calculate the charge, potential difference and energy stored in the capacitor separately.
View SolutionCapacitor C1=2μFandC2=3μF are connected in series to a battery of emf ε=120V whose midpoint is earthed. The wire connecting the capacitors can be earthed through a key K. Now, key K is closed. Determine the charge flowing through the sections 1, 2, and 3 in the directions indicated in figure
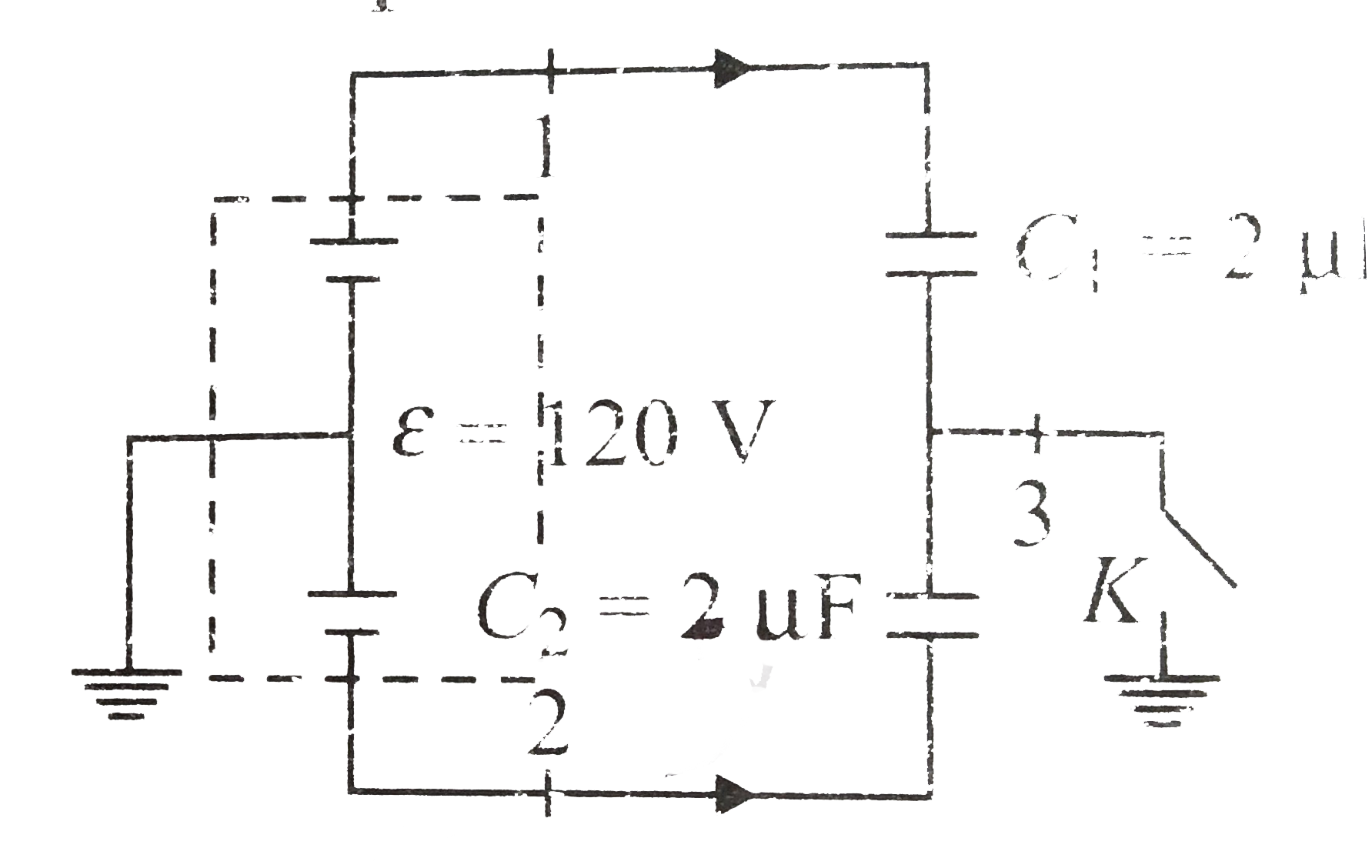
In section 2,
View SolutionCapacitor C1=2μFandC2=3μF are connected in series to a battery of emf ε=120V whose midpoint is earthed. The wire connecting the capacitors can be earthed through a key K. Now, key K is closed. Determine the charge flowing through the sections 1, 2, and 3 in the directions indicated in figure

In section 3,
View SolutionThree capacitors C1=3μF,C2=6μFandC3=10μF are connected to a 50 V battery as shown in the figure below:
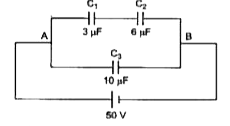
Calculate :
The equivalent capacitance of the circuit between points A and B.
View Solution