Let ABCD is a rectangle with AB=a & BC=b & circle is drawn passing through A & B and touching side CD. Another circle is drawn passing thorugh B & C and touching side AD. Let r1 & r2 be the radii of these two circle respectively.
r1r2 equals
ab(4b2+a24a2+b2)
ba(4a2+b(2)4b2+a2)
ab(4b2−a24a2−b2)
ba(a2−4b24a2−b2)
The correct Answer is:A
To solve the problem, we need to find the ratio of the radii r1 and r2 of the two circles drawn in rectangle ABCD.
Step 1: Define the Geometry
Let AB=a and BC=b. The first circle passes through points A and B and touches side CD. The second circle passes through points B and C and touches side AD.
Step 2: Analyze the First Circle
Let the center of the first circle be O1 and the radius be r1. The distance from O1 to line CD is r1. The distance from O1 to point B is r1 as well.
In triangle O1MB (where M is the midpoint of AB):
- MB=a2
- The height from O1 to line CD is r1−b.
Using the Pythagorean theorem:
r21=(r1−b)2+(a2)2
Step 3: Expand and Simplify
Expanding the equation:
r21=(r21−2br1+b2)+a24
Cancelling r21 from both sides:
0=−2br1+b2+a24
Rearranging gives:
2br1=b2+a24
Thus,
r1=b2+a242b=4b2+a28b
Step 4: Analyze the Second Circle
Let the center of the second circle be O2 and the radius be r2. The distance from O2 to line AD is r2. The distance from O2 to point C is r2 as well.
In triangle O2CN (where N is the midpoint of BC):
- CN=b2
- The height from O2 to line AD is A−r2.
Using the Pythagorean theorem:
r22=(A−r2)2+(b2)2
Step 5: Expand and Simplify
Expanding the equation:
r22=(A2−2Ar2+r22)+b24
Cancelling r22 from both sides:
0=−2Ar2+A2+b24
Rearranging gives:
2Ar2=A2+b24
Thus,
r2=A2+b242A=4A2+b28A
Step 6: Find the Ratio r1r2
Now, we can find the ratio:
r1r2=4b2+a28b4a2+b28a=(4b2+a2)⋅a(4a2+b2)⋅b
Final Result
Thus, the ratio r1r2 is:
r1r2=a(4b2+a2)b(4a2+b2)
Let AB=a and BC=b. The first circle passes through points A and B and touches side CD. The second circle passes through points B and C and touches side AD.
Let the center of the first circle be O1 and the radius be r1. The distance from O1 to line CD is r1. The distance from O1 to point B is r1 as well.
- MB=a2
- The height from O1 to line CD is r1−b.
r21=(r1−b)2+(a2)2
Expanding the equation:
r21=(r21−2br1+b2)+a24
Cancelling r21 from both sides:
0=−2br1+b2+a24
Rearranging gives:
2br1=b2+a24
Thus,
r1=b2+a242b=4b2+a28b
Let the center of the second circle be O2 and the radius be r2. The distance from O2 to line AD is r2. The distance from O2 to point C is r2 as well.
- CN=b2
- The height from O2 to line AD is A−r2.
r22=(A−r2)2+(b2)2
Expanding the equation:
r22=(A2−2Ar2+r22)+b24
Cancelling r22 from both sides:
0=−2Ar2+A2+b24
Rearranging gives:
2Ar2=A2+b24
Thus,
r2=A2+b242A=4A2+b28A
Now, we can find the ratio:
r1r2=4b2+a28b4a2+b28a=(4b2+a2)⋅a(4a2+b2)⋅b
Thus, the ratio r1r2 is:
r1r2=a(4b2+a2)b(4a2+b2)
Similar Questions
Let ABCD is a rectangle with AB=a & BC=b & circle is drawn passing through A & B and touching side CD. Another circle is drawn passing through B & C and touching side AD. Let r1 & r2 be the radii of these two circle respectively.
Minimum value of (r1+r2 equals
View SolutionThe equation of the circle passing through (2,1) and touching the coordinate axes is
View SolutionIf the radius of the circle passing through the origin and touching the line x+y=2 at (1,1) is r units, then the value of 3√2r is
View SolutionConsider circles C1andC2 touching both the axes and passing through (4,4), then the product of the radii of the two circles is
View SolutionA circle passes through (0,0) and (1,0) and touches the circle x2+y2=9 then the centre of circle is -
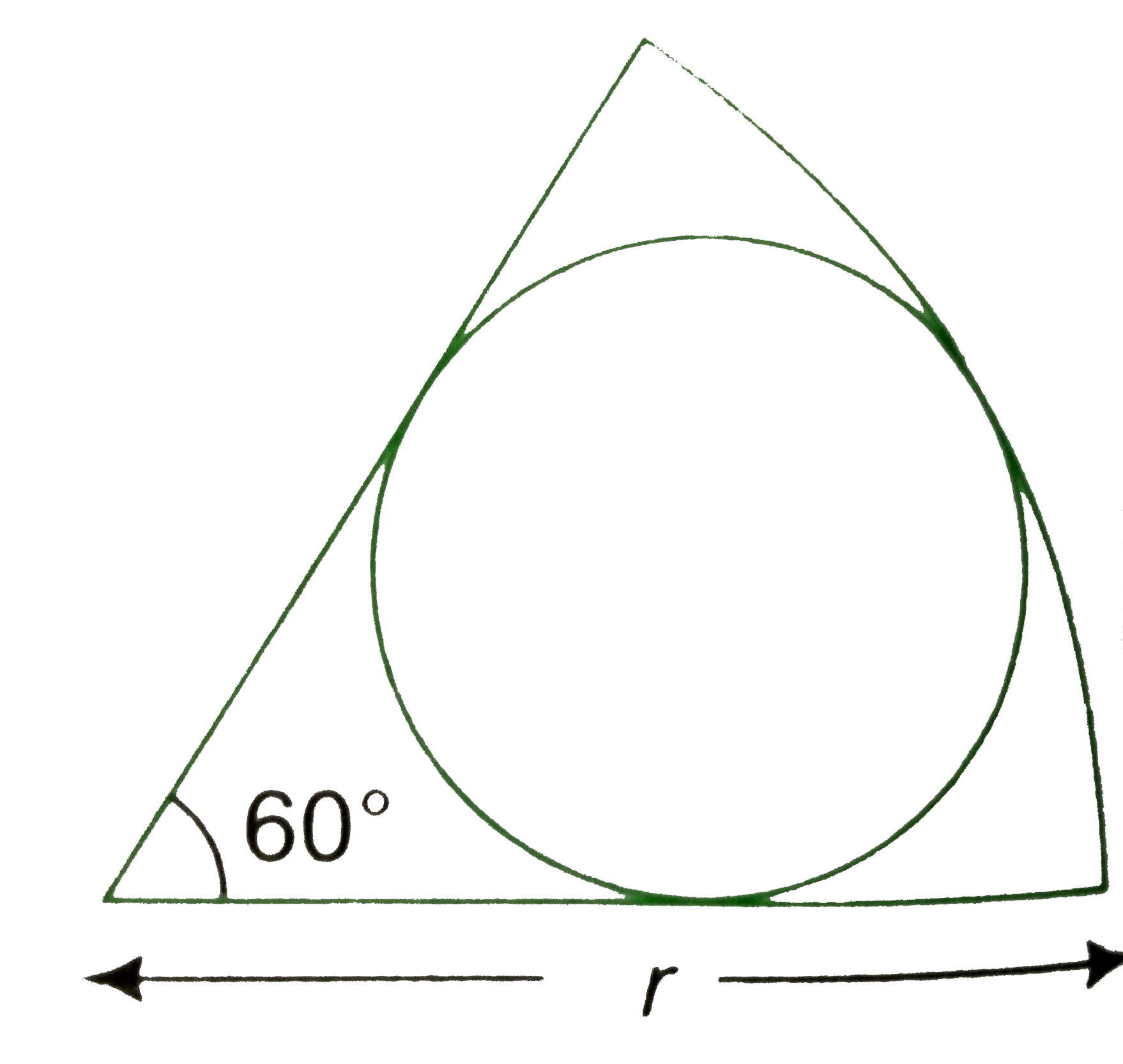
View SolutionA circle is drawn in a sectore of a larger circle of radius r, as shown in fugure. The smaller circle is tangent to the two bounding radii and the are of the sector. The radius of the smaller circle is
View SolutionABCD is a parallelogram . The circle passing through the vertices. A, B and C intersects CD (or CD produced) at E. Prove that AE=AD.
View SolutionLet ABC be a triangle right-angled at AandS be its circumcircle. Let S1 be the circle touching the lines AB and AC and the circle S internally. Further, let S2 be the circle touching the lines AB and AC produced and the circle S externally. If r1 and r2 are the radii of the circles S1 and S2 , respectively, show that r1r2=4 area (ABC).
View SolutionA circle is drawn in a sector of a larger circle of radius r, as shown in the adjacent figure. The smaller circle is tangent to the two bounding radii and the are of the sector. The radius of the small circle is-

View SolutionIf radii of the smallest and the largest circle passing through (√3,√2) and touching the circle x2+y2−2√2y−2=0 are r1 and r2 respectively, then find the mean of r1 and r2.
View Solution
